高中毕业会考数学试卷
一、选择题：本大题共20个小题，每小题2分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
（1）设全集
，集合
，
，则
（ ）
（A）
（B）
（C）
（D）
（2）
的值等于（ ）
（A）
（B）
（C） 
（D）
（3）函数
，
R的最小正周期是（ ）
（A）
（B）
（C）
（D）
（4）已知向量
，
，则
的坐标是（ ）
（A）（2，6） （B）（6，2） （C）（8，－2） （D）（－8，２）
（5）经过点(1,－3)，且倾斜角的正切值为
的直线的方程是（ ）
（A）
（B）
（C）
（D）
（6）函数
的反函数是（ ）
（A）
（B）
（C） （D）
（7）下列函数中为奇函数的是（ ）
（A）
（B）
（C）
（D）
（8）双曲线 
的渐近线的方程是（ ）
（A）
（B）
（C）
（D）
（9）抛物线 
的焦点坐标是（ ）
（A）（－1，0） （B）（1，0） （C）（0，－1） （D）（0，1）
(10) 已知等比数列
中, 
, 
, 则
的值为（ ）
（A）
（B）
（C）
（D）
（11）
的值为（ ）
（A）15 （B）24 （C）30 （D）360
（12）在正方体ABCD-A1B
（A）30° （B）45° （C）60° （D）90°
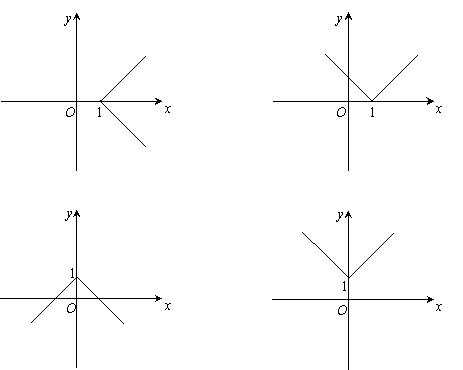（13）函数
的图象大致是（ ）
（A） （B）
（C） （D）
（14）若
R，且
，则下列结论成立的是（ ）
（A）
（B）
（C）
（D）
（15）在空间，下列命题中正确的是（ ）
（A）垂直于同一直线的两条直线平行 （B）垂直于同一平面的两个平面平行
（C）平行于同一直线的两个平面平行 （D）平行于同一平面的两个平面平行
（16）圆心为（3，4），且经过坐标原点的圆的方程是（ ）
（A）
（B）
（C）
（D）
（17）要得到函数
R的图象，只需将函数
R图象上所有的点（ ）
（A）向左平行移动
个单位长度 （B）向右平行移动个单位长度
（C）向左平行移动
个单位长度 （D）向右平行移动个单位长度
（18）函数
的定义域为（ ）
（A）
（B）
（C）
（D）
（19）已知
，
，且
，
，则
的值等于（ ）
（A）
（B）
（C）
（D）
（20）已知函数
，且
，
，则有（ ）
（A）
（B）
（C）
（D）
与
的大小不确定
二、填空题：本大题共6个小题，每小题3分，共18分． 请将答案填在题中横线上．
（21）已知一个球的表面积是
cm2，则它的半径等于
cm．
（22） 经过点A（3，0），且与直线
垂直的直线方程的一般式为
．
（23）已知
, 则
的值是
．
（24）已知
，
,
和
的夹角是
，则
的值等于
．
（25）在△
中，已知
，
，
，则
的值是
．
（26）星期一上午的四节课要安排数学、物理、化学、生物各一节，则不同的安排方法
共有 种(用数字作答)．
三、解答题：本大题共5个小题,共42分．解答应写出文字说明、演算步骤或推理过程．
(27) (本小题满分8分)已知
. 试求下列各式的值：
（Ⅰ）
；（Ⅱ）
．
(28)(本小题满分8分)解不等式 
．
(29)(本小题满分8分)已知等差数列
中，
，
,
求：（I）首项
和公差
；（II）该数列的前8项的和
的值．
(30)(本小题满分8分)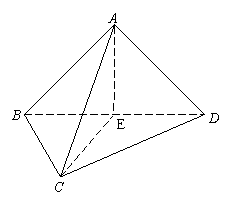
如图，在三棱锥A—BCD中，侧面ABD与底面BCD均为等腰直角三角形，
， E为BD的中点，且
．
（Ⅰ）求证：
底面
；
（Ⅱ）若
，求三棱锥A—BCD的体积．
(31)
(本小题满分10分)已知椭圆的方程为
，直线
经过椭圆的焦点与椭圆交于A、B两点，若△
的面积为
，求直线的方程．
高中毕业会考数学试卷参考答案
一、选择题：ABDCD CAABC ADCBD ABDCA
二、填空题：（21）3 （22）
（23）－2 （24）
（25）
（26）24
三、解答题：本大题共5个小题，满分42分．
（27）本小题满分8分．解
(Ⅰ) ∵ ， ∴ cos
．
|
|
（28）本小题满分8分．
解 原不等式可以化为：
． 由数轴标根法，有
得原不等式的解集为 
. 8分
（29）本小题满分8分．
解 (Ⅰ) 由等差数列
的通项公式： 
=
，
得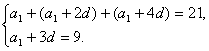
解得 =3，=2. 4分
(Ⅱ) 由等差数列的前
项和公式：
，
6分
得 
.
8分
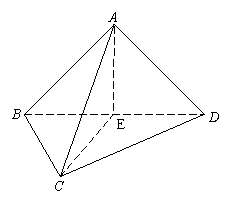
（30）本小题满分8分．
（Ⅰ）证明 已知△ABD是等腰直角三角形，∠BAD=90°，
且E为BD的中点，∴ AE⊥BD． 2分
又∵AE⊥CE， BD与CE均在平面BCD内，
且BD
CE=E，
∴AE⊥平面BCD． 4分
（Ⅱ）解 在Rt△ABD中，斜边BD=2，
|
BD=1．同理 CE=1．
由（Ⅰ）的结论：AE⊥平面BCD，
得AE为三棱锥A—BCD的高．
（31）本小题满分10分．
解 由椭圆的方程，得 
∴ 椭圆的焦点为
（0，－1）， 
（0，1）．
2分
据题意，当直线经过焦点（0，1）时，
可设其方程为 
，
3分
建立方程组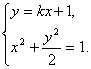 
消去y ，得
4分
若
则
∴ 
∴
. 
又原点O到直线的距离为
，
由已知，可得 
解得 
∴ 经过焦点（0， 1 ）时，直线的方程为 
；
同理，经过焦点（0， －1 ）时，直线的方程为 
． 10分