高中二年级教学下期质量监测
数学(理)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题的四个选项中只有一个是正确的,请把正确选项填在答题卡相应位置。
1. 已知集合A=![]() ,B=
,B=![]() ,则满足
,则满足![]() 的实数a的一个值为( )
的实数a的一个值为( )
A. 0 B.
2. 若直线![]() 与直线
与直线![]() 互相垂直,则a的值为( )
互相垂直,则a的值为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
3. 在![]() 的展开式中第四项为( )
的展开式中第四项为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
20
D.
20
4. 函数![]() 的单调递增区间是( )
的单调递增区间是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
5. 在等差数列![]() 中,
中,![]() ,则其前n项和最大时n的值为( )
,则其前n项和最大时n的值为( )
A. 11 B.
6. 函数![]() 的图象大致是( )
的图象大致是( )
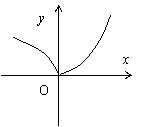
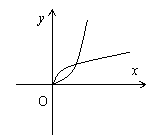
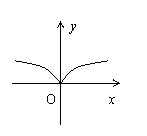
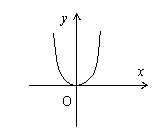
A B C D
7. 将3个不同的小球随意放入4个不同的盒子里,则3个小球恰在3个不同的盒子内的概率为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
8. 三条直线a,b,c两两相交且不共点,命题:
① 平行于a、b的平面平行于直线c;②垂直于a、b的直线垂直于直线c;③与三个交点等距离的平面平行于直线a、b、c;④其中假命题的个数为( )
A. 0 B.
9. 在△ABC中,已知![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B.
![]() D.
D.
![]()
10. 6人排成一排,甲、乙两人必须相邻且丙在乙的右边,则不同的排法种数为( )
A. 120 B.
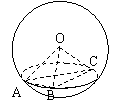
11. 如图A、B、C是表面积为![]() 的球面上三点,AB=2,BC= 4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角为( )
的球面上三点,AB=2,BC= 4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角为( )
 A.
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
12. 甲袋中装有3个白球和5个黑球,乙袋中装有4个白球和6个黑球,现从甲袋中随机取出一个球放入乙袋中,充分混合后,再从乙袋中随机取出一个球放回甲袋中,则甲袋中白球没有减少的概率为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
二、填空题:本大题共4个小题,每小题4分,满分16分,把答案直接填在题中横线上。
13. 在![]() 的展开式中,所有各项的系数和为__________.
的展开式中,所有各项的系数和为__________.
14. 已知![]() ,
,![]() 满足约束条件
满足约束条件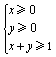 ,则
,则![]() 的最小值为_____________.
的最小值为_____________.
15. 对某种产品的6件不同正品和4件不同次品一一进行测试,直到区分出所有次品为止,若所有次品恰好在第五次测试被全部发现,则这样的测试方法有______________种。
16. 在棱长为a的正方体骨架内放置一气球,使其充气且尽可能膨胀(仍保持为球的形状),则气球表面积的最大值为________________.
三、解答题:本大题共6个小题,满分74分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)设![]() ,
,![]() ,
,![]()
(1)求证:![]() ;
;
(2)求![]() 的最大值及对应的x的值。
的最大值及对应的x的值。
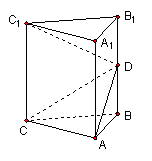
18. (本小题满分12分)如图,直三棱柱ABC-A1B![]() AA1,∠BAC=90°,D为棱BB1的中点。
AA1,∠BAC=90°,D为棱BB1的中点。
(1)求异面直线C1D与A
(2)求证:平面A1DC⊥平面ADC.
19. (本小题满分12分)甲、乙、丙3人各进行1次射击,若3人击中目标的概率分别是![]() ,
,![]() ,
,![]() .求:
.求:
(1)3人中至少有1人击中目标的概率;
(2)若3人同时射击,恰有1人击中目标的概率;
(3)乙至少要射击几次才能使击中目标的概率大于98%.(参考数据:![]() )
)
20. (本小题满分12分)若等差数列![]() 的首项为
的首项为![]() (
(![]() ),公差是
),公差是![]() 展开式中的常数项,其中
展开式中的常数项,其中![]() 为
为![]() 除以19的余数,求数列
除以19的余数,求数列![]() 的通项公式.
的通项公式.
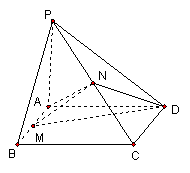
21. (本小题满分12分)如图,已知ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=2,PD=AB,且平面MND⊥平面PCD.
(1)求证:MN⊥AB;
(2)求二面角P-CD-A的大小;
(3)求三棱锥D-AMN的体积。
22. (本小题满分14分)已知双曲线C:![]() 的两个焦点分别为
的两个焦点分别为![]() ,且
,且![]() .又双曲线C上任意一点E满足
.又双曲线C上任意一点E满足![]() .
.
(1)求双曲线C的方程;
(2)若双曲线C上的点P满足![]() ,求
,求![]() 的值;
的值;
(3)若直线![]() 与双曲线C交于不同的两点M、N,且线段MN的垂直平分线过点A
与双曲线C交于不同的两点M、N,且线段MN的垂直平分线过点A![]() ,求实数m的取值范围.
,求实数m的取值范围.