高中高二统一考试数学试题
第Ⅰ卷(选择题共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1、解答应用题的步骤实际也是一种算法,其最后一步是( )
A.列式计算 B.总结归纳 C.检验结果 D.作答
2、某工厂生产产品,用传送带将产品送至下一工序,质检人员每隔十分钟在传送带某一位置取一件检验,则这种抽样方法是( )
A.简单随机抽样 B.系统抽样 C.分层抽样 D.非上述抽样
3、为了解所加工的一批零件的长度,抽测了其中 200 个零件的长度。在这个问题中,200个零件的长度是( )
A.总体 B.个体 C.总体的一个样本 D.样本容量
4、已知变量 a、b 已被赋值,要交换 a、b 的值,则应采用 的算法。( )
A. a←b,b←a B. a←c,b←a,c←b
C. a←c,b←a,c←a D. c←a,a←b,b←c
5、为了解 1200 名学生对学校某项教改试验的意见,打算从中抽取一个容量为30的样本,考虑采用系统抽样,则分段的间隔(抽样距)k 为( )
A.40 B.30 C.20 D.12
6、对于样本频率分布直方图与总体密度曲线的关系,下列说法正确的是( )
A.频率分布直方图与总体密度曲线无关
B.频率分布直方图就是总体密度曲线
C.样本容量很大的频率分布直方图就是总体密度曲线
D.如果样本容量无限增大,分组的组距无限减小,那么频率分布直方图就会无限接近总体密度曲线
7、如果数据![]() 的平均数是 x ,方差是
的平均数是 x ,方差是![]() ,则
,则![]() 的平均数和方差分别是( )
的平均数和方差分别是( )
A.![]() 与
与![]() B.2
B.2 ![]() +3 和
+3 和![]() C. 2
C. 2 ![]() +3 和 4
+3 和 4![]() D. 2
D. 2![]() +3 和 4
+3 和 4![]() +12S+9
+12S+9
8、设有一个直线回归方程![]() =2-1.5x ,则变量 x 增加一个单位( )
=2-1.5x ,则变量 x 增加一个单位( )
A. y 平均增加 1.5 个单位 B. y 平均增加 2 个单位
C. y 平均减少 1.5 个单位 D. y 平均减少 2 个单位
|
A.1 B.2 C.3 D.4
10、根据如图所示的伪代码,可知输出结果为( )
A.17 B.19
C.21 D.23
11、某人从湖中打了一网鱼,共 m 条,做上记号再放入湖中,数日后又打了一网鱼共 有 n 条,其中 k 条有记号。试估计湖中共有鱼 条。( )
 A.
A.![]() B. m
B. m ![]() C. m
C. m ![]() D.
无法估计
D.
无法估计
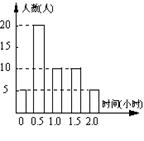
12、某校为了了解学生课外阅读情况,随机调查了 50 名
学生,得到他们在某一天各自阅读所用时间的数据,结果用右边的条形图表示。根据条形图可得这 50名学生平均每天课外阅读时间为( )
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(4'×6=24')
13、下面程序语句执行后的输出是 i= ,
j= . i ←5 ,j ←-2 ,i ← i+j ,j ← i+j
14、先后抛两枚硬币,则两次均为正面向上的概率为 .
|
测得他们在最大速度(m/s)的数据的基时图如右图所示,
![]()
![]() 试问哪一位运动员较为优秀? .
试问哪一位运动员较为优秀? .
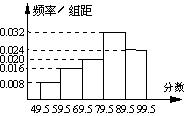 17、对某班学生一次英语测试的成绩分析,各数据段的分布如图(分数取整数),由此估计这次测验的优秀率(不小于80分)为
。
17、对某班学生一次英语测试的成绩分析,各数据段的分布如图(分数取整数),由此估计这次测验的优秀率(不小于80分)为
。
18、某企业三月中旬生产 A、B、C 三种产品共
3000件,根据分层抽样的结果,企业统计员制作了如下的统计表格:
| 产品类别 | A | B | C |
| 产品数量(件) | 1300 | ||
| 样本容量 | 130 |
由于不小心,表格中A、C产品的有关数据已被污染看不清楚,统计员只记得A产品的样本容量比C产品的样本容量多10,请你根据以上信息填补表格中数据。
三、解答题:(共66分)
![]()
20、 设计一个计算某班(50人)的一次数学考试的平均分的算法,并画出相应的流程图,书写伪代码。(13')
![]()
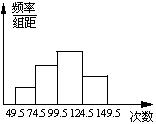 22、为了了解小学生的体能情况,抽取了某校一个年
22、为了了解小学生的体能情况,抽取了某校一个年
级的部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),已知图中从左到右前三个小组的频率分别为 0.1,0.3,0.4,
第一小组的频数为 5. (12')
⑴求第四小组的频率; ⑵参加这次测试的学生有多少?
⑶若次数在 75 次以上(含75 次)为达标,试估计该年级学生跳绳测试的达标率.
23、有一个容量为 20 的样本,其数据如下(单位:岁) (15')
44 45 29 42 58 37 53 52 49 34
27 32 42 55 40 38 50 26 54 26
⑴填写以下的频率分布表;
⑵绘出频率分布图(用铅笔绘制)和折线图(在同一幅图中作);
⑶据频率分布图的各组中值估计总体平均数,并将所得结果与实际的总体平均数相比较,计算误差。
| 分组 | 频数 | 频率 | 频率\组踞 |
| [19.5,29.5] |
|
|
|
| [29.5,39.5] |
|
|
|
| [39.5,49.5] |
|
|
|
| 49.5,59.5] |
|
|
|
| 合计 |
|
|
|
高中高二统一考试数学试题参考答案
一. 选择题(共60分)
DBCDA DCCDA BB
二. 填空题(共24分)
13.
3 , 1
14. ![]() 15. 乙
15. 乙
16.
50
三.解答题(共66分)
19.(本小题12分)
解: 流程图:
 |
![]()
![]() Y
N
N
Y
N
N
 | |||||||
Y
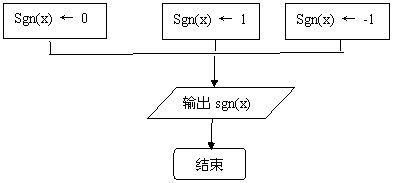 |
伪代码:
Read x
If x=0 then
Sgn(x)←0
Else
If x>0 then
Sgn(x)←1
Else
Sgn(x)←-1
End if
Print Sgn(x)
20.(本小题13分)
解:
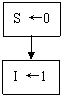
算法:
S1 S←0
S2 I←1
S3 输入GI
S4 S←S+GI
S5 I←I+1
S6
如果I![]() 50,转为S3;
50,转为S3;
否则,退出循环.
S![]()
S8 输出A
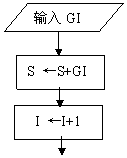
伪代码:
S←0
For I from 1 to 50 step 1
Read GI
S←S+GI
End for
A←![]()
Print S
流程图:
 |
![]()
![]()
![]()
 |
![]() N
N
![]() Y
Y
 |
21.(本小题14分)
伪代码:
S←0
a←1
For I from 1 to 100 step 1
S←S+![]()
a←a*(-1)
End for
Print S
流程图:
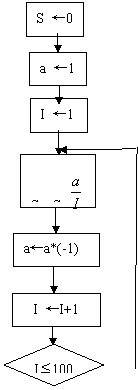 |
Y
![]()
![]() N
N
22.(本小题12分)
(1) 0.2 (2) 50 (3) 0.9
23.(本小题15分)
(1)
| 分组 | 频数 | 频率 | 频率\组踞 |
| [19.5,29.5] | 4 | 0.2 | 0.02 |
| [29.5,39.5] | 4 | 0.2 | 0.02 |
| [39.5,49.5] | 6 | 0.3 | 0.03 |
| 49.5,59.5] | 6 | 0.3 | 0.03 |
| 合计 | 20 | 1 | 0.1 |
(2)
![]() 频率\组踞
频率\组踞
0.03
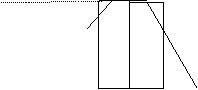 |
![]()
![]()
![]()
![]()
![]() 0.02
0.02
![]()
19.5 39.5 9.5
(3)组中值:41.5 实际 : 41.65
误差:0.15