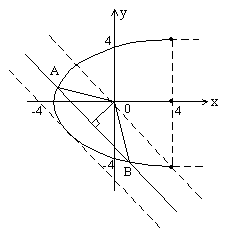高中数学会考模拟试题（一）
一. 选择题：（每小题2分，共40分）
1. 已知I为全集，P、Q为非空集合，且
，则下列结论不正确的是（ ）
A. 
B. 
C. 
D. 
2. 若
，则
（ ）
A. 
B. 
C. 
D. 
3. 椭圆
上一点P到两焦点的距离之积为m。则当m取最大值时，点P的坐标是（ ）
A. 
和
B.
和
C. 
和
D.
和
4. 函数
的最小正周期是（ ）
A. 
B. 
C. 
D. 
5. 直线
与两条直线
，
分别交于P、Q两点。线段PQ的中点坐标为
，那么直线的斜率是（ ）
A. 
B. 
C. 
D. 
6. 为了得到函数
，
的图象，只需将函数
，的图象上所有的点（ ）
A. 向左平行移动
个单位长度 B.
向右平行移动个单位长度
C. 向左平行移动
个单位长度 D.
向右平行移动个单位长度
7. 在正方体
中，面对角线
与体对角线
所成角等于（ ）
A. 
B. 
C. 
D. 
8. 如果
，则在① 
，② 
，③ 
，④ 
中，正确的只有（ ）
A. ②和③ B. ①和③ C. ③和④ D. ②和④
9. 如果
，
，而且
，那么
的值是（ ）
A. 4 B. 
C. 
D. 
10. 在等差数列
中，
，
，则
等于（ ）
A. 19 B. 50 C. 100 D. 120
11. 
，且
是
成立的（ ）
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
12. 设函数
，
，则（ ）
A. 
是奇函数，
是偶函数 B.
是偶函数，是奇函数
C. 和都是奇函数 D.
和都是偶函数
13. 在
中，已知
，
，
，则
等于（ ）
A. 3或9 B. 6或9 C. 3或6 D. 6
14. 函数
的反函数是（ ）
A. 
B.
C. 
D.
15. 若
，
，则（ ）
A. 在R上是增函数 B.
在
上是增函数
C. 在
上是减函数 D.
在上是减函数
16. 不等式
的解集是（ ）
A. {
或
} B.
{
}
C. {
} D.
{或}
17. 把4名中学生分别推荐到3所不同的大学去学习，每个大学至少收一名，全部分完，不同的分配方案数为（ ）
A. 12 B. 24 C. 36 D. 28
18. 若、
是异面直线，则一定存在两个平行平面
、
，使（ ）
A. 
，
B.
，
C. 
， D.
，
19. 将函数
按平移后，得到
，则
（ ）
A. 
B. 
C. 
D. 
20. 已知函数，，且
，当时，是增函数，设
，
，
，则、的大小顺序是（ ）
A. 
B. 
C. 
D. 
二. 填空题（每小题3分，共18分）
21. 已知是与
的等比中项，且
，则
22. 计算
的值等于
23. 由数字1，2，3，4可以组成没有重复数字比1999大的数共有 个
24. 不等式
的解集是
25. 半球内有一内接正方体，正方体的一个面在半球的底面圆上，若正方体的一边长为
，则半球的体积是
26. 点P是双曲线
上任意一点，则P到二渐近线距离的乘积是
三. 解答题（共5个小题，共42分）
27.（8分）设
，
求
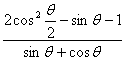的值
28.（8分）解不等式
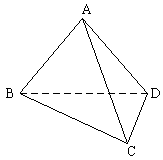
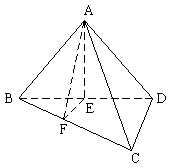
29.（8分）已知三棱锥
，平面
平面
，AB=AD=1，AB⊥AD，DB=DC，DB⊥DC
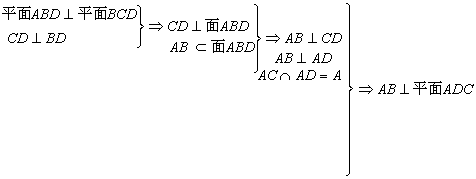
（1）求证：AB⊥平面ADC
（2）求二面角
的大小
（3）求三棱锥的体积
30.（8分）已知数列中，
是它的前
项和，并且
，
。
（1）设
，求证
是等比数列
（2）设
，求证
是等差数列
（3）求数列的通项公式及前项和公式
31.（10分）已知直线：
和曲线C：
（1）直线与曲线C相交于两点，求m的取值范围
（2）设直线与曲线C相交于A、B，求
面积的最大值
【试题答案】
一.
1. C 2. B 3. C 4. B 5. C 6. C 7. D 8. D 9. D 10. C
11. D 12. B 13. C 14. C 15. B 16. D 17. C 18. A 19. C 20. B
二.
21. 3 22. 
23. 18 24. 
25. 
26. 3
三.
27.
解：
原式
28.
解：根据题意：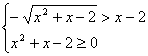
由
得：
∴ 
由
得：
或
∴ 原不等式的解集为{
或}
29.
（1）
证明：
（2）
解：取BD中点E，连结AE，过A作AF⊥BC，F为垂足，连结EF
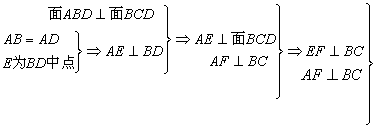
是二面角的平面角
在
中，
，
∴ 
在
中，
∴ 
（3）
30.
解：
（1）
∴ 
∴ 
即：
且
∴ 是等比数列
（2）的通项
∴ 
又
∴ 为等差数列
（3）∵ 
∴ 
∴ 
∴ 
31.
解：
（1）∵ 
∴
过点
与平行的直线为
即
∵ 与C有两个交点 ∴ 
由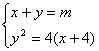
得
∵ 与C有两交点 ∴ 
即
∴ 
综上所述，m的取值范围为
（2）将
代入中，得
∴ 
又
∴ 
∴ 
最大值
