高二数学期中试卷
一、选择题：本大题共12小题，每小题5分，满分60分． 在每小题给出的四个选项中，有且只有一项是符合题目要求的．
1、若n∈N*，则（20-n）(21-n)……(100-n)等于（ ）
A．
B．
C．
D．
2、若从集合P到集合Q={a,b,c}所有不同的映射共有81个，则从集合Q到集合P可作的不同的映射共有（ ）
A．32个 B．64个 C．81个 D．27个
3、在
的展开式中，各项系数和是（ ）
A．1
B．-1
C．-1或1 D．
4、一个容量为20的样本数据，分组后，组距与频数如下：（10，20），2；（20，30），3；
（30，40），4；（40，50），5；（60，70），6；则样本在（
）上的频率为（
）
A、
B、
C、
D、
5、一个骰子连续掷两次，以先后得到的点数m，n为点P (m，n)，那么点P在圆x2 + y2 = 17内部的概率为（ ）
A．
B．
C．
D．
6、（理科）已知离散型随机变量ξ的分布列为
| ξ | 0 | 1 |
| P |
|
|
则c的值为（ ）
A．
B． 
C．或
D．
(文科) 一个样本的方差是
，则这个样本的平均数与样本容量分别是（ ）
A．15，10 B．6，15
C．10．10
D．由
确定，10
7、设袋中有80个红球，20个白球。若从袋中任取10个球，则其中恰如有6个红球的概率为 （ ）
A、
B、
C、
D、
8、三位同学各自独立解一道题，他们能解出的概率分别为1/5，1/3，1/4。现在三人合作学习，能将此题解出的概率是（ ）
A．
B．
C．
D． 
9、书架上有排好顺序的6本书，如果保持这6本书的相对顺序不变，再放上3本书，则不同的放法种数为（ ）
A．505种 B．252种 C．210种 D．504种
10、（理科）已知如果随机变量
，若
，则
（ ）
A．1-
B．
C．1-2 D．
(文科) 从甲、乙两种玉米苗中各抽10株，测得它们的株高分别如下：（单位：cm）
| 甲 | 25 | 41 | 40 | 37 | 22 | 14 | 19 | 39 | 21 | 42 |
| 乙 | 27 | 16 | 44 | 27 | 44 | 16 | 40 | 40 | 16 | 40 |
根据以上数据估计（ ）
A．甲种玉米比乙种玉米不仅长得高而且长得整齐
B．乙种玉米比甲种玉米长得高但长势没有甲整齐
C．甲种玉米比乙种玉米长得高但长势没有乙整齐
D．乙种玉米比甲种玉米不仅长得高而且长得整齐
11、从－1，0，1，2，3这五个数中选三个不同的数组成二次函数 y=ax2＋bx＋c的系数，在所得二次函数的图象中，与x轴的正半轴、负半轴各有一个交点的抛物线有（ ）
A．9条 B．18条 C．24条 D．36条
12、由等式
定义
，则
等于
（ ）
A、
B、
C、
D、
二、填空题：本大题共4小题，每小题4分，满分16分．
13、5555－1除以8所得的余数是 。
14、（理科）现有甲种电脑56台，乙种电脑42台，如果用分层抽样的方法从中抽取一个容量为14的样本，则乙种电脑应抽样_ ___台．
(文科) 某中学高中一年级有400人，高中二年级有320人，高中三年级有280人，以每人被抽取的概率为0.2向该中学抽取一个容量为n的样本，则n= 。
15、将一个各个面上均涂有颜色的正方体锯成27个同样大小的小正方体，从这些小正方体中任取一个，其中恰有2面涂有颜色的概率是 ．
16、关于二项式(x-1)2005有下列命题：
①该二项展开式中非常数项的系数和是1： ②该二项展开式中第六项为C
x1999；
③该二项展开式中系数最大的项是第1002项：④当x=2006时，(x-1)2005除以2006的余数是2005．其中正确命题的序号是__________ ． (注：把你认为正确的命题序号都填上)
三、解答题：本大题共6小题，共74分．解答应写出文字说明、演算步骤或推证过程.
17、（本小题满分12分）已知
展开式中的倒数第三项的系数为45。
求：⑴含x3的项； ⑵系数最大的项。
18、（本小题满分12分）有5名男生，4名女生排成一排：
（1）从中选出3人排成一排，有多少种排法？
（2）若男生甲不站排头，女生乙不站在排尾，则有多少种不同的排法？
（3）要求女生必须站在一起，则有多少种不同的排法？
（4）若4名女生互不相邻，则有多少种不同的排法？
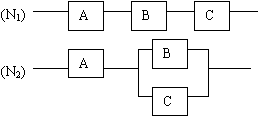19、（本小题满分12分）（本小题满分12分）如图，用A、B、C三 类不同的无件连接成两个系统N1、N2，当元件A、B、C都正常工作时，系统N1正常工作；当元件A正常工作且元件B、C至少有一个正常工作时，系统N2正常工作，已知元件A、B、C正常工作的概率依次为0.80，0.90，0.90，分别求系统N1、N2正常工作的概率P1、P2。
20、（本小题满分12分）某研究性学习小组的6位同学借助互联网查资料，每位同学上网的概率都是0.5（相互独立），问：
（1）至少3位同学同时上网的概率是多少？
（2）至少几位同学同时上网的概率小于0.3？
21、（理科）（本小题满分12分）甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6道题，乙能答对其中的8道题. 规定每位考生都从备选题中随机抽出3道题进行测试，至少答对2题才算合格.
（Ⅰ）求甲答对试题数
的概率分布及数学期望和方差；
（Ⅱ）求甲、乙两人至少有一人考试合格的概率.
（文科）（本小题满分12分）某单位最近组织了一次健身活动，活动分为登山组和游泳组，且每个职工至多参加了其中一组
在参加活动的职工中，青年人占425％，中年人占47
5％，老年人占10％ 登山组的职工占参加活动总人数的
，且该组中，青年人占50％，中年人占40％，老年人占10％ 为了了解各组不同的年龄层次的职工对本次活动的满意程度，现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本 试确定
（Ⅰ）游泳组中，青年人、中年人、老年人分别所占的比例；
（Ⅱ）游泳组中，青年人、中年人、老年人分别应抽取的人数
22、（本小题满分14分）有6名男医生，4名女医生。
（Ⅰ）选3名男医生，2名女医生，让这5名医生到5个不同地区去巡回医疗，共有多少种分派方法？
（Ⅱ）把10名医生分成两组，每组5人且每组要有女医生，则有多少种不同分法？若将这两组医生分派到两地去，并且每组选出正副组长两人，又有多少种分派方案？
高二数学期中考试答题卷
| 题号 | 一 |
| 三
17 18 19 20 21 22 | 总分 |
| 得分 |
|
|
|
|
二一．选择题：本大题共12小题；每小题5分，共60分．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二．填空题：本大题共4小题；每小题4分，共16分．
13．____________________ 14．____________________
15．____________________ 16．____________________
三．解答题：本大题共6小题，共74分．解答应写出必要的文字说明、证明过程及演算步骤．
17、（本小题满分12分）已知 展开式中的倒数第三项的系数为45。
求：⑴含x3的项； ⑵系数最大的项。
18、（本小题满分12分）有5名男生，4名女生排成一排：
（1）从中选出3人排成一排，有多少种排法？
（2）若男生甲不站排头，女生乙不站在排尾，则有多少种不同的排法？
（3）要求女生必须站在一起，则有多少种不同的排法？
（4）若4名女生互不相邻，则有多少种不同的排法？
19、（本小题满分12分）如图，用A、B、C三 类不同的无件连接成两个系统N1、N2，当元件A、B、C都正常工作时，系统N1正常工作；当元件A正常工作且元件B、C至少有一个正常工作时，系统N2正常工作，已知元件A、B、C正常工作的概率依次为0.80，0.90，0.90，分别求系统N1、N2正常工作的概率P1、P2。
20、（本小题满分12分）某研究性学习小组的6位同学借助互联网查资料，每位同学上网的概率都是0.5（相互独立），问：（1）至少3位同学同时上网的概率是多少？
（2）至少几位同学同时上网的概率小于0.3？
21、（理科）（本小题满分12分）甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6道题，乙能答对其中的8道题. 规定每位考生都从备选题中随机抽出3道题进行测试，至少答对2题才算合格.（Ⅰ）求甲答对试题数的概率分布及数学期望和方差；
（Ⅱ）求甲、乙两人至少有一人考试合格的概率.
（文科）（本小题满分12分）某单位最近组织了一次健身活动，活动分为登山组和游泳组，且每个职工至多参加了其中一组 在参加活动的职工中，青年人占425％，中年人占47
5％，老年人占10％ 登山组的职工占参加活动总人数的，且该组中，青年人占50％，中年人占40％，老年人占10％ 为了了解各组不同的年龄层次的职工对本次活动的满意程度，现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本 试确定（Ⅰ）游泳组中，青年人、中年人、老年人分别所占的比例；
（Ⅱ）游泳组中，青年人、中年人、老年人分别应抽取的人数
22、（本小题满分14分）有6名男医生，4名女医生。
（Ⅰ）选3名男医生，2名女医生，让这5名医生到5个不同地区去巡回医疗，共有多少种分派方法？
（Ⅱ）把10名医生分成两组，每组5人且每组要有女医生，则有多少种不同分法？若将这两组医生分派到两地去，并且每组选出正副组长两人，又有多少种分派方案？