高二数学上册期末测试

高二数学上册期末测试

一、选择题（本大题共10小题，每小题5分，共50分）

1．下列命题正确的是　　　　　　　　　　　　　　　　　　　　　　　　 　　 （　　）

　　　A．若，则　　　 B．若，则

　　C．若，则　　　 D．若，则

2．如果直线与直线平行，那么系数的值是　　　　　　　　（　　）

　　A．－3　　　　　　　 B．－6　　　　　　 C．　 　　　　　　　 D．

3．与双曲线有共同的渐近线，且过点（2，2）的双曲线方程为　　　　　　（　　）

　　A．　　　 B． 　　 C． 　　　D．

4．下说法正确的有　 ①对任意实数a、b,都有a+b+a－b2a;

②函数y=x·(0<x<1)的最大函数值为　③对aR,不等式x<a的解集是{x－a<x<a};

④ 若AB≠0,则．

A． ①②③④　　　　 B．②③④　　　　　 C．②④　　　　 　 D．①④　　　（　　）

5．直线过点P(0,2),且被圆x²+y²=4截得弦长为2,则的斜率为　　　　　　  　（　　）

A．　　  　　　 B．　 　　　　　 C．　　　　 D．

6．若椭圆(a＞b＞0)的左、右焦点分别为F₁、F₂，线段F₁F₂被抛物线y²=2bx的焦点

分成5∶3的两段，则此椭圆的离心率为　　　　　　　　　　　　　　 　　　（　　）

　　　A．　　　　  　 B．　　 　　　 C．　　　　　　 D．

7．已知不等式的解集为（—∞，—1）∪（3，+∞），则对于函数

，下列不等式成立的是　　　　　　　　　　　　　 （　　）

A．　 B．　 C．　　　　　　 D．

8．已知直线，则抛物线上到直线距离最小的点的坐标为　　　　　 （　　）

　　　 A．　　 　　　B．　　　 　　C．　　 　　　D．

9．设z=x-y, 式中变量x和y满足条件， 则z的最小值为　　　　  　　　 （　　）

　　　 A．1　　　　　  　 B．-1　 　　　　　 C．3　　　　　　　　　D．-3

10．已知椭圆E的离心率为e，两焦点为F₁，F₂. 抛物线C以F₁为顶点，F₂为焦点.P为两曲线的一

个交点.若,则e的值为　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　 B．　　　　　　C．　　 D．

二、填空题（本大题共4小题，每小题4分，共16分）

11．设中心在原点的椭圆与双曲线2x²－2y²=1有公共的焦点，且它们的离心率互为倒数，则该椭圆的方程是　　　　　 ．

12．已知两变量，之间的关系为，则以为自变量的函数的最小值为________．

13．直线经过直线的交点，且与直线的夹角为45°，则直线方程的一般式为　　　　　　　 .

14．已知下列四个命题：

①在直角坐标系中，如果点P在曲线上，则P点坐标一定满足这曲线方程的解；

②平面内与两个定点F₁，F₂的距离的差的绝对值等于常数的点的轨迹叫做双曲线；

③角α一定是直线的倾斜角；

④直线关于轴对称的直线方程为.

其中正确命题的序号是 　　　　　　　（注：把你认为正确命题的序号都填上）

三、解答题　 15．解不等式.　　 18．解关于x的不等式

16．已知圆与直线交于、两点，若线段的中点

（1）求直线的方程；　（2）求弦的长．（12分）

17（12分）P为椭圆上一点，、为左右焦点，若

（1）　　　 求△的面积；　（2）求P点的坐标．（12分）

19.已知，，，；（1）比较与的大小；

（2）设，,求证：．

　

20．过抛物线y²=2px(p>0)的焦点F的直线与抛物线交于A、B两点,O为坐标原点,直线OA

的斜率为,直线OB的斜率为.　　　（1）求·的值；

（2）过A　B两点向准线做垂线,垂足分别为、,求的大小．（12分）

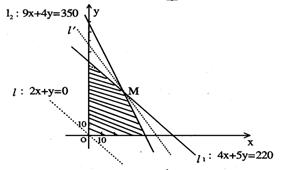
21．某厂生产甲、乙两种产品，生产每吨甲、乙产品所需煤、电力和所获利润如下表所示：

消耗量　 资源 产品	煤（t）	电力（kW）	利润（万元）
甲产品	9	4	12
乙产品	4	5	6

在生产这两种产品中，要求用煤量不超过350t，电力不超过220kW.问每天生产甲、乙两种产品各多少，

能使利润总额达到最大？（12分）

22．已知双曲线的中心在原点，右顶点为A(1,0)，点P、Q在双曲线的右支上，点M(m,0)到直线AP

的距离为1．（1）若直线AP的斜率为k，且kÎ[], 求实数m的取值范围；

（2）当m=+1时，△APQ的内心恰好是点M，求此双曲线的方程．（14分）

　

 

 

23．如图，已知的直角顶点为，点，点在轴上，点在轴负半轴上，在的延长线上取一点，使．　 （1）B在轴上移动时，求动点的轨迹；

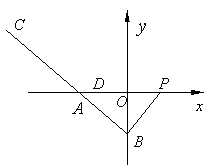（2）若直线与轨迹交于、两点，设点，当为锐角时，求的取值范围．（14分）

参考答案

一、选择题（本大题共10小题，每小题5分，共50分）

题号	1	2	3	4	5	6	7	8	9	10
答案	D	B	D	A	B	D	A	B	A	A

二、填空题11． 　12．　　4　　　 13． 　　14． ① ④

三、解答题15．当时，原不等式可化为:,解得,即,

　　　　 则原不等式的解为:;当时，原不等式可化为:，该不等式恒成立

　　 所以，原不等式的解为.

16．（12分）[解析]： （1），

　　．

　　 （2）原点到直线的距离为，．

17.[解析]：∵a＝5，b＝3c＝4  （1）设，，则　①

　②，由①²－②得　　

　　　　

（2）设P，由得  4，

将 代入椭圆方程解得，或或或

18[解析]：原不等式. 分情况讨论

（i）当a＜0或a＞1时，有a＜a²，此时不等式的解集为；

（ii）当时，有a²＜a，此时不等式组的解集为

（iii）当a=0或a=1时，原不等式无解．

综上，当a＜0或a＞1时时，原不等式的解集为；

当时，原不等式的解集为

当a=0或a=1时，原不等式的解集为φ.

19..[解析]：．(1)

　 　即 .

(2)由（1）

=

． 得证．

20．[解析]：．设A()，B)，则，，

∵直线AB过焦点F,若直线AB与x轴不垂直，∴可设AB方程为：y=k（），代入抛物线方程有

，可得·=，则·=－p²，

∴·=；若直线AB与x轴垂直,得=2, ,∴·=－4

(2) 如图，∵ A、B在抛物线上，∴ AF=AA₁　 ∴∠AA₁F=∠AFA₁，∴∠AFA₁=

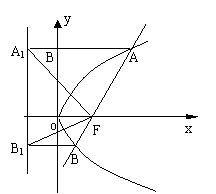同理

∴

90^o ，

又，

.

21．[解析]：设每天生产甲、乙两钟产品分别为t、t，

利润总额为z万元.那么：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　

z=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

作出以上不等式组所表示的平面区域，即可行域

，作出以上不等式组所表示的平面

区域，即可行域（如右图）.　作直线，

把直线向右上方平移至位置时，直线经过可行域上点M，现与原点距离最大，此时z=取最大值.

解方程组　 得M（30，20）　　答：生产甲产品30t，乙产品20t，能使利润总额达到最大.

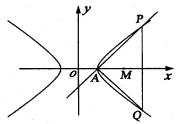22．[解析]：（1） 由条件得直线AP的方程，即kx－y－k=0，　因为点M到直线AP的距离为1，

（2）可设双曲线方程为，

由又因为M是 的内心，M到AP的距离为1，所以直线AM是的角平分线，且M到AQ、PQ的距离均为1，因此，（不妨设A在第一象限），直线PQ的方程为，直线AP的方程为

所以解得点P的坐标为，将其代入得，所求双曲线的方程为，即.

23．[解析]：设

　

　

　（２）令把

　，

结合图形可得