高二数学上学期(理科)期末试卷
版本: 苏教版 测试范围:必修3、选修2-1第1、2章及选修2-2第1章
![]()
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分200分。考试时间150分钟。
参考公式:
三角函数的和差化积公式
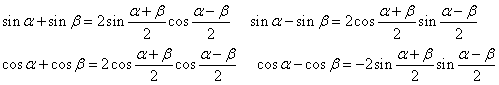 一组数据
一组数据![]() 的方差
的方差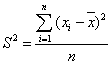 ,其中
,其中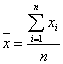 为这组数据的平均数值。
为这组数据的平均数值。
设线性回归方程为![]() ,则系数a,b满足
,则系数a,b满足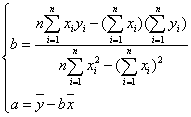
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.一个容量为32的样本,已知某组样本的频率为0.125,则该组样本的频数为 A.2 B
2.下列几个图形在流程图中分别代表什么框?
 |
①,②,③,④分别代表
A. 处理框,起止框,输入、输出框,判断框
B. 起止框,输入、输出框, 处理框,判断框
C. 起止框, 处理框,输入、输出框,判断框
D. 输入、输出框, 处理框,起止框,判断框
3.从甲、乙、丙三人中任选两名代表,甲被选中的概率是 ( )
A.![]() B.
B. ![]() C.
C.
![]() D.1
D.1
4.顶点在原点,焦点是(0,-2)的抛物线方程是 ( )
A. ![]() B.
B. ![]() C.
C.![]() D.
D. ![]()
5.设![]()
A.0
B.
6.下列命题中正确的是 ( )
①“若x2+y2≠0,则x,y不全为零”的否命题
②“正多边形都相似”的逆命题
③“若m>0,则x2+x-m=0有实根”的逆否命题
④“若x=![]() ,则x是无理数”的逆否命题
,则x是无理数”的逆否命题
A、①②③④ B、①③④ C、②③④ D、①④
7.平面内有定点A、B及动点P,设命题甲是“PA+PB是定值”,命题乙是“点P的轨迹是以A、B为焦点的椭圆”,那么甲是乙的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
8.P是长轴在x轴上的椭圆![]() 上的点,
上的点,![]() 分别为椭圆的两个焦点,椭圆的半焦距为c,则
分别为椭圆的两个焦点,椭圆的半焦距为c,则![]() 的最大值与最小值之差一定是
( )
的最大值与最小值之差一定是
( )
A.1
B.![]() C.
C.![]() D.
D.![]()
9.双曲线![]()
![]() 上一点P(a,b)到直线y=x的距离为
上一点P(a,b)到直线y=x的距离为![]() ,
,
则a+b的值 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
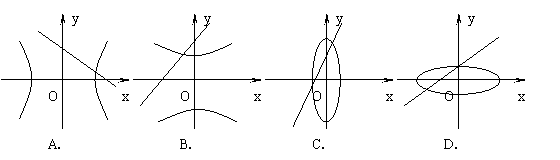
10.方程![]() 和
和![]() (
(![]() 是不为零的实数)所表示的曲线草图只可能
( )
是不为零的实数)所表示的曲线草图只可能
( )
11、已知函数![]() (导函数)的取值范围是( )
(导函数)的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对
12.曲线![]() 在原点处的切线方程为 ( )
在原点处的切线方程为 ( )
A.y = 1275x B, y =
502x C ,y =
100x
D. y = 50!x
二.填空题:本大题共有6小题,每小题5分,共30分.把答案填在题中横线上.
13.八个数据1,2,4,5,7,8,10,11的平均数是 ▲
14.命题 “![]() ”的否定是 ▲
”的否定是 ▲
15.动点P(x,y)到直线x=5的距离与它到点F(1,0)的距离之比为![]() ,
,
则动点P的轨迹为 ▲
16.过原点作曲线![]() 的切线,则切点的坐标为 ▲
的切线,则切点的坐标为 ▲
17. 已知双曲线![]() (a>0,b>0)的离心率e=
(a>0,b>0)的离心率e=![]() (“优美双曲线”),A、F分别是它的左顶点和右焦点,设点B的坐标为(0,b),则
(“优美双曲线”),A、F分别是它的左顶点和右焦点,设点B的坐标为(0,b),则
∠ABF等于 ▲
18、对正整数n,设曲线![]() 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为![]() ,则数列
,则数列![]() 的前n项和的公式是 ▲
的前n项和的公式是 ▲
三.解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
19.(本题满分12分,每问4分)将一颗骰子先后抛掷2次,观察向上的点数,问:
(1)两数之和为6的概率;
(2)两数之和是3的倍数的概率;
(3)两数之积是6的倍数的概率。
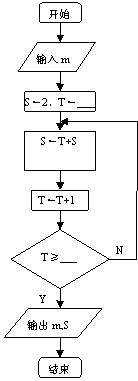 20.(本题满分10分,每空2分,算法6分)已知数列
20.(本题满分10分,每空2分,算法6分)已知数列![]() 中,
中,![]() ,且
,且![]()
![]() ,求这个数列的第m项
,求这个数列的第m项![]() 的值
的值![]() 。
。
现给出此算法流程图的一部分,请将空格部分(两个)填上适当的内容,并用“For”循环语句写出对应的算法。
21.(12分)如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
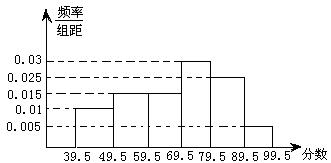
(1)79.5---89.5这一组的频数分别是多少?
(2)估计这次环保知识竞赛的及格率(60分及以上为及格)
22.(12分)某单位决定投资3200元建一个形状为长方体的仓库,高度一定,它的后墙利用旧墙不用花钱,正面用铁栅,每米造价为40元,两侧墙砌砖,每米造价45元,屋顶每平方米造价20元,设铁栅的长为x米,两侧墙各为y米,
(1)试写出x,y满足的条件;
(2)仓库面积S的最大允许值是多少平方米?
23.(12分)设函数![]() 分别在
分别在![]() 处取得极小值、极大值。
处取得极小值、极大值。![]() 平面上点
平面上点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 。该平面上动点
。该平面上动点![]() 满足
满足![]() ,点
,点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点。求:
的对称点。求:
(1)
点![]() ,
,![]() 的坐标;
的坐标;
(2)
求动点![]() 的轨迹方程。
的轨迹方程。
24.(12分)已知双曲线的两条渐近线为![]() ,且一个顶点的坐标为
,且一个顶点的坐标为
![]() .
.
(1)求双曲线的方程;
(2)是否存在过![]() 的一条直线交双曲线与M、N两点,且线段MN被直线x=-1平分.如果存在,求出这条直线的方程;如果不存在,说明理由.
的一条直线交双曲线与M、N两点,且线段MN被直线x=-1平分.如果存在,求出这条直线的方程;如果不存在,说明理由.
四、附加题(1-4题每题5分,第5小题8分,第6小题12分,共40分):
1.定积分![]() 的值是 ( )
的值是 ( )
A.1
B
2.已知![]() ,则它可能是( )
,则它可能是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知![]() ,则f(x)是_ __▲___.
,则f(x)是_ __▲___.
4.已知![]() ,则
,则![]() __▲__.
__▲__.
5.求曲线![]() 与直线y=2x所围成的图形的面积.
与直线y=2x所围成的图形的面积.
6.我们把底面为正方形的长方体称为正四棱柱。
(1)求底面边长为
(2)已知锥体的体积![]() ,其中r为圆锥的底面半径,h为圆锥的高,试用“分割——近似代替——作和——逼近”思想求出球的体积公式。
,其中r为圆锥的底面半径,h为圆锥的高,试用“分割——近似代替——作和——逼近”思想求出球的体积公式。
(3)求半径为R球的内接圆锥的体积的最大值。
高二数学试卷
(必修3、选修2-1前两章及选修2-2导数)
(时间150分钟,满分200分)2006-秋学期 命题、校对:柳金爱
参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | C | D | B | B | B | D | B | B | A | D |
二、填空题
13、_6_
; 14、 ![]() ; 15、椭圆;
; 15、椭圆;
16、![]() ; 17、
; 17、![]() ;
18、
;
18、![]()
三、解答题
19.解:由课本列表可知;
(1)两数之和为6的概率为![]() ; (2)两数之和是3的倍数的概率为
; (2)两数之和是3的倍数的概率为![]() ;
;
(3)此问题中含有36个等可能基本事件,记“向上的两数之积是6的倍数”为事件A,则由下面的列表可知,事件A中含有其中的15个等可能基本事件,所以P(A)=![]() ,
,
 答:两数之积是6的倍数的概率为
答:两数之积是6的倍数的概率为![]() 。
。
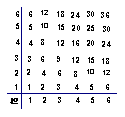 20.解:2,m+1;
20.解:2,m+1;
21.【解】(1)因为频率为:0.025×10=0.25,所以频数为:60×0.25=15
(2)0.015×10+0.025×10+0.03×10+0.005×10=0.75,即![]() ;
;
22.解:
(1)依题意,S=xy,且x>0,y>0,40x+90y+20xy=3200即4x+9y+2xy=320,
所以x,y满足的条件是4x+9y+2xy=320,x>0,y>0.
(2) 方法1:(代入消去x)由4x+9y+2xy=320得到,![]() ,设t=y+2,∵x,y>0,∴0<y<
,设t=y+2,∵x,y>0,∴0<y<![]() ,
,![]()
![]() ( 当且仅当t=
( 当且仅当t=![]() 时,等号成立)
时,等号成立)
∴S=![]()
∴当t=![]() ,即
,即![]() ,x=15时,S取得最大值100;
,x=15时,S取得最大值100;
方法2:(代入消去y)
由4x+9y+2xy=320得到,![]() ,设t=2x+9,∵x,y>0,∴0<x<80,2x=t-9,
,设t=2x+9,∵x,y>0,∴0<x<80,2x=t-9,
∴![]() ,
,
∵![]() (当且仅当t=39时等号成立),
(当且仅当t=39时等号成立),
∴![]()
![]() ,∴当t=39,即x=15,
,∴当t=39,即x=15,
![]() 时,S取得最大值100;
时,S取得最大值100;
方法3:(求导法)由4x+9y+2xy=320得到,![]() ,
,
∵x,y>0,∴0<x<80,![]()
于是![]()
令![]()
又x>0,得0<x<15时,![]() ,x>15时,
,x>15时,![]() ,从而x=15时,S取最大值100
,从而x=15时,S取最大值100![]() 。
。
方法4:∵x,y>0,∴4x+9y≥12![]() (当且仅当4x=9y时,取“=”),
(当且仅当4x=9y时,取“=”),
又4x+9y+2xy=320,∴![]() ,即
,即![]() ,解得0<
,解得0<![]() ,∴S =xy≤100, ∴当4x=9y,即x=15,
,∴S =xy≤100, ∴当4x=9y,即x=15, ![]() 时,S取得最大值100;
时,S取得最大值100;
答:仓库面积的最大允许值为100平方米。
23.解: (Ⅰ)令![]() 解得
解得![]()
当![]() 时,
时,![]() , 当
, 当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以,函数在![]() 处取得极小值,在
处取得极小值,在![]() 取得极大值,故
取得极大值,故
![]() ,
,![]()
所以, 点A、B的坐标为![]() .
.
(Ⅱ) 设![]() ,
,![]() ,
,
![]()
方法1:(Ⅱ) 设![]() ,
,![]() ,
,
![]()
![]() ,所以
,所以![]() ,又PQ的中点在
,又PQ的中点在![]() 上,所以
上,所以![]()
消去![]() 得
得![]()
方法2:![]() 的轨迹是圆,
的轨迹是圆,![]() 只需求出圆心(0,2)关于直线y=2(x-4)的对称点(8,-2)即可,容易求出
只需求出圆心(0,2)关于直线y=2(x-4)的对称点(8,-2)即可,容易求出![]()
24. 【解】(1)![]() ;
;
(2)设所求的直线l存在,则其斜率必存在,设其方程为![]() ,代入双曲线方程消去y,得
,代入双曲线方程消去y,得
![]() ,所以
,所以![]() 且
且
![]() ,所以
,所以![]() .若MN被x= -1平分,则
.若MN被x= -1平分,则![]() 相矛盾.所以所求直线不存在.
相矛盾.所以所求直线不存在.
四、附加题参考答案提示(满分40分):
1. D 2. B 3. ![]() 4. 1
4. 1
5.解:由题意,解方程![]() ,得
,得![]()
于是![]()
6.解:(1)![]() ;
;
(2) 提示:以球心为顶点,把球的表面分割成n个小的底面(以点代面),
利用“分割——近似代替——作和——逼近”思想可求出球的体积公式为![]()
(3) ![]()
![]() 22
22