高二数学
上学期期中测试
时量：100分钟 满分：100分
一、选择题（每小题4分，共28分）
1.设
为等差数列,其中
（ ）
A.24 B.
2. 设为等比数列,其中
（ ）
A.25 B.
3.
中,若
,则C=
（ ）
A.
B.
C.
D.
4.在锐角中,若
,则第三边
应满足的条件是
（ ）
A.
B.
C.
D.
5.在中,若
,则是
（ ）
A.正三角形 B.等腰三角形 C.直角三角形 D.等腰直角三角形
6.已知
,则必有
（ ）
A.
B.
C.
D.
7.某林场原有木材存量为
,木材每年以25%的增长率生长,而每年要砍掉的木材量为
,为了实现经过两年达到木材存量的1.5倍,则
（ ）
A. 
B.
C. 
D. 
请务必将选择题的答案写在下面：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
|
二、填空题（每小题4分，共24分）
8.在中,若
,则
_____________________.
9.不等式
的解集是
.
10.若
的最小值是 .
11.在等差数列中,
.
12.设、
满足约束条件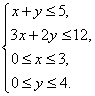
则目标函数
的最大值是 .
13.已知数列的前
项和
,则的通项公式为 .
三、解答题（第14、15题9分，16～18题每题10分，共48分）
14.设为等差数列,公差
成等比数列,求
和
.
15.在中,若
,试求的面积.
16.已知数列的前项和
, (1)求证:为等差数列;(2)求数列
的前项和
.
17.在数列中,已知
,求
和一个通项公式.
18. (1)已知关于的不等式
<1的解集为R,求实数的取值范围.
(2)设
且
,求
的最小值,并求
取得最小值的
的值.
高二数学上学期期中测试
(参考答案)
时量：100分钟 满分：100分
一、选择题答案：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| A | A | A | C | B | D | D |
二、填空题（每小题4分，共24分）
8.
9. 
10、4 11., -2 .12、27 .13、
三、解答题（第14、15题9分，16～18题每题10分，共48分）
14、解:由题设,得
,从而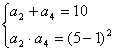
…………………………………..(4分)
解得
…………………………………………………(7分)
由此得
…………………………………………………(8分)
故
……………………………………………………..(9分)
15、解:由正弦定理,得
…………………… .(2分)
从而
…………………………………………………… (3分)
于是
……………………………………………………. .(4分)
由三角形面积公式,得
…………
.(6分)
当
;………………………………………………. (7分)
当
…………………………………………………. (8分)
故的面积是
…………………………………………….. (9分)
16、解:(1)当
时,
……(2分).
当
时,
也满足上式……………………………………(3分)
所以
………………………………………………………………………(4分)
因为
…………………………………………(6分)
所以为以3为首项2为公差的等差数列………………………………………(7分)
(2)因为
所以
=
=
=
……………………………….(10分)
17、解:
, 
, 
, 
,
…………………………………………………………..(4分)
当
时, 
…….
………………………………………………(8分)
当时, 
也满足上式………………………………………………..(9分)
故数列的通项公式是
……………………………………….(10分)
或解一: 当时, 由
及
两式相减,得: 
……………………………………….(6分)
所以数列
是首项为
公比为8的等比数列.所以
…………………………………………………(7分)
将代入上式,并整理得
…………………………..(8分)
当时, 也满足上式………………………………………………..(9分)
故数列的通项公式是……………………………………….(10分)
或解二: 当时, 由得
………….(6分)
所以数列
是首项为
公比为8的等比数列
所以
…………………………………………………(7分)
所以……………………………………………………………….(8分)
当时, 也满足上式………………………………………………..(9分)
故数列的通项公式是……………………………………….(10分
18、解: <1,
整理,得
…………………………………………………(1分)
依题,得
,
即
整理,得
………………………………………………………..(3分)
解得
………………………………………………………………….(5分)
因此实数的取值范围是………………………………………….(6分)
(2)设且,求的最小值,并求取得最小值的的值.
解: 
当
,又,即
时,等号成立……………..(9分)因此取得最小值是
…………………………………………………….(10分)