高二数学数列单元测试题

高二数学数列单元测试题

一、选择题

1．等差数列前10项和为100，前100项和为10。则前110项的和为

A．-90　　　　　　  B．90　　　　　　  C．-110　　　　　　  D．10

2．两个等差数列，它们的前n项和之比为，则这两个数列的第9项之比是

A．　　　　　　  B．　　　　　　  C．　　　　　　  D．

3．若数列中，=43-3n，则最大值n=

A．13　　　　　　  B．14　　　　　　  C．15　　　　　　  D．14或15

4．一个项数为偶数的等差数列，奇数项的和与偶数项的和分别为24和30。若最后一项超过第一项10.5，则该数列的项数为

A．18　　　　　　  B．12　　　　　　  C．10　　　　　　  D．8

5．等差数列的前m项的和是30，前2m项的和是100，则它的前3m项的和是

A．130　　　　　　  B．170　　　　　　  C．210　　　　　　  D．260

6．等差数列中，，=4 ，若有=9，则k=

A．2　　　　　　  B．3　　　　　　  C．4　　　　　　  D．5

7．等比数列中，已知，则n为

A．3　　　　　　  B．4　　　　　　  C．5　　　 　　　 D．6

8．等比数列中，，则等于

A．3　　　　　　  B．　　　　　　  C．　　　　　　  D．4

9．等差数列的首项，公差，如果成等比数列，那么等于

A．3　　　　　　  B．2　　　　　　  C．－2　　　　　　  D．

10．设由正数组成的等比数列，公比q=2，且，则等于

A．　 　　　　　 B．　　　　　　  C．　　　　　　  D．

二、填空题

1．等差数列中=25，=405。则=______________。

2．等差数列5，8，11，……与等差数列3，8，13，……都有100项，那么这两个数列相同的项共有______________项。

3．等差数列中，=40， =13，d=-2 时，n=______________。

4．小于200的自然数中被7除余3的所有的数的和是______________。

5．等比数列满足，则______________。

6．在等比数列中，，则______________，______________。

7．等比数列的公比为2，前4项之和等于10，则前8项之和等于______________。

三、解答题

1．已知等差数列中，=q，= p，求

2．已知a,b,c成等差数列。求证:,,是等差数列。

3．一个等比数列中，，求这个数列的通项公式。

4．有四个数：前三个成等差数列，后三个成等比数列。首末两数和为16，中间两数和为12。求这四个数。

5．等差数列的前n项和。求数列的前n项的和。

6． 数列中,当n为奇数时,,当n为偶数时,=,若数列共有2m

项。求这个数列的前2m项的和。

高中数学 第三章 测试卷 参考答案

一、选择题

题号	1	2	3	4	5
答案	C	C	B	D	C
题号	6	7	8	9	10
答案	D	B	D	B	B

二、填空题

题号	1	2		3		4
答案	475	20		4或10		2929
题号	6		7		8
答案	或2		-2，10		170

三、解答题

1．答案: a_p-a_q= q-p=(p-q)d,d= -1. a_p+q=a_p+qd=q-q=0

2．答案:把()+()中的a+c代换为2b=a+c,

推导出:()+()=2 ().

所以:, ,是等差数列.

3．答案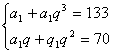：两式相除得，代入，

　　　　　　　可求得或8，

　　　　　　　

4．答案：设此四数为：x，y，12-y，16-x。所以2y=x+12-y且（12-y）²　= y（16-x）。

　　 把x=3y-12代入，得y= 4或9。解得四数为15，9，3，1或0，4，8，16。

5．答案：该等差数列为-21，-13，-5，3，11，……前3项为负，其和为－39。

　

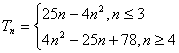
6．答案:该数列为:6,2,16,4,26,8,……，6+（m-1）×10，2  ^m ，

　　S _2m =[6+16+26+……+6+（m-1）×10]+[ 2¹ +2 ²+2  ³+……+2  ^m]

　　　  =5m²+m+2 ^m+1 －2。