高二数学同步测试—双曲线
1．到两定点
、
的距离之差的绝对值等于6的点
的轨迹 （ ）
A．椭圆 B．线段 C．双曲线 D．两条射线
2．方程
表示双曲线，则
的取值范围是 （ ）
A．
B．
C．
D．
或
3． 双曲线
的焦距是 （ ）
A．4 B．
C．8 D．与
有关
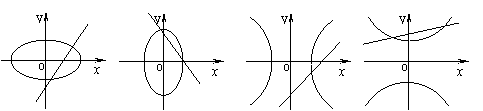4．已知m,n为两个不相等的非零实数，则方程mx－y+n=0与nx2+my2=mn所表示的曲线可能是 （ ）
A B C D
6．焦点为
，且与双曲线
有相同的渐近线的双曲线方程是 （ ）
A．
B．
C．
D．
7．若
，双曲线
与双曲线
有 （ ）
A．相同的虚轴 B．相同的实轴 C．相同的渐近线 D． 相同的焦点
8．过双曲线
左焦点F1的弦AB长为6，则
（F2为右焦点）的周长是（ ）
A．28 B．22 C．14 D．12
9．已知双曲线方程为
，过P（1，0）的直线L与双曲线只有一个公共点，则L
的条数共有 A．4条 B．3条 C．2条 D．1条 （ ）
10．给出下列曲线：①4x+2y－1=0;
②x2+y2=3;
③
④
，其中与直线y=－2x－3
有交点的所有曲线是 A．①③ B．②④ C．①②③ D．②③④ （ ）
13．直线
与双曲线
相交于
两点，则
=
14．过点
且被点M平分的双曲线
的弦所在直线方程为
1.求证：双曲线
（
）与双曲线
有共同的渐近线.
2.求与双曲线
有共同的渐近线且经过点
的双曲线方程
3.已知双曲线的渐近线方程为
，实轴长为12，求它的标准方程.
4．求一条渐近线方程是
，一个焦点是
的双曲线标准方程，并求此双曲线的离心率．（12分）
5．已知不论b取何实数，直线y=kx+b与双曲线
总有公共点，试求实数k的取值范围.（12分）
6．某中心接到其正东、正西、正北方向三个观测点的报告：正西、正北两个观测点同时听到了一声巨响，正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上).（14分）
参考答案
一、选择题（本大题共10小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | D | C | C | B | B | D | A | B | D |
二、填空题（本大题共4小题，每小题6分，共24分）
11．
12．
13．
14．
三、解答题（本大题共6题，共76分）
15． [解析]：设双曲线方程为：
，
∵双曲线有一个焦点为（4，0），
双曲线方程化为：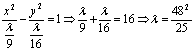
，
∴双曲线方程为：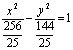
∴
．
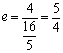18． [解析]：联立方程组
消去y得
(2k2－1)x2+4kbx+（2b2+1）=0,
当
若b=0，则k
；
若
，不合题意.
当
依题意有
△=(4kb)2－4(2k2－1)(2b2+1)＞0，
对所有实数b恒成立，
∴2k2<1，得
.
20．（14分）[解析]：以接报中心为原点O，正东、正北方向为x轴、y轴正向，建立直角坐标系.设A、B、C分别是西、东、北观测点，则A（－1020，0），B（1020，0），C（0，1020）
设P（x,y）为巨响为生点，由A、C同时听到巨响声，得PA=PB，故P在AC的垂直平分线PO上，PO的方程为y=－x，因B点比A点晚4s听到爆炸声，故PB－ PA=340×4=1360
由双曲线定义知P点在以A、B为焦点的双曲线
上， 依题意得a=680, c=1020，
用y=－x代入上式，得
，∵PB>PA,
,答：巨响发生在接报中心的西偏北45°距中心
处.