高二数学同步辅导教程

高二数学同步辅导教程

期末复习测试题

一、选择题

1、下列数列中，极限为1的是（　　 ）

（A）{a_n} ：a_n=　　　　　  （B）{a_n} ：a_n= (－0.99)ⁿ

（C）{a_n} ：a_n=　　 （D）{a_n} ：a_n =

2、若向量垂直于向量和向量，=λ+u(λ,u∈R,且λu≠0), 则（　 ）

（A）∥　　  （B）⊥　　  （C）不平行,也不垂直于

（D）以上三种情况都有可能

3、正方体的全面积是24，则其外接球的体积为（　　）

（A）24π　　　（B）π　　 （C）8π　　　（D）4π

4、从6名志原者中，选出4人分别从事翻译、导游、导购、保洁四项不同的工作，若其中甲、乙两名志愿者不能从事翻译工作，则不同的选派方案共有（　　）

（A）280种　　　（B）240种　　　（C）180种　　 （D）96种

5、从5名男同学和3名女同学中选出4位代表，其中至少有2位男同学，且至少有1位女同学的不同选法共有（　　 ）

（A）100种　　　（B）90种　　 （C）95种　　 （D）60种

6、某次智力测验有6道基础知识题和4道能力提高题。每个抽答4题，基础知识题答对1题给1分，能力题答对1题给2分。要使所选题的总分值不低于7分，所选的答题方式有（　　）

（A）15种　　 （B）25种　　 （C）210种　　（D）80种

7、把靶时，甲的命中率为为0.8，乙的命中率为0.7，若两人同时射击一个目标，则他们都中靶的概率是（　　）

（A）0.38　　　 （B）0.24　　  （C）0.56　　 （D）0.94

8、在(1－x)³(1+x)¹⁰的展开式中，含x⁵项的系数是（　　）

（A）－297　　  （B） －252　　 （C）297　　（D）207

9、的展开式中，无理数项的个数是（　　）

（A）84　　  （B）85　　　（C）86　　  （D）87

10、摇奖器摇出的一组中奖号码为8，2，5，3，7，1.从0，1，2，……，9这十个数字中任意选出六个不同的数字组成一组。如果选出的六个数字中至少有五个与摇奖器摇出的号码相同（不计顺序）就可以得奖。则中奖的概率为（　　）

（A）　　　 （B）　　（C）　　  （D）

11、在4次独立重复试验中，随机事件A恰好发生一次的概率不大于其恰好发生两次的概率，则事件A在一次试验中发生的概率P的取值范围是（　　 ）

（A）[0.4, 1　　　　（B）0,　0.4 ]　　　　 （C）0, 0.6 ]　　 （D）[ 0.6,1

12、任意写一个无重复数字的三位数，其中十位上的数字最小的概率是（　　）

（A）　　  （B）　　（C）　　 （D）

二、填空题

13、三棱锥的三个侧面与底面均成60⁰的二面角，底面三角形的三边长分别为3，4，5，则这三个棱锥的侧面积为______________.

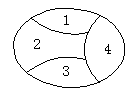14、用五种不同颜色给图中41个区域涂色，

如果每一个区域涂一种颜色，相邻两区

域不能涂同一种颜色，共有_________

种不同的涂色方法.

15、有一道数学难题，在半小时内，甲能解决的概率是乙能解决的概率是，两人试图独立地在半小时内解决它。则难道在半小题的内得到解决的概率为__________.

16、已知(2x+)⁴ =a₀+a₁x+a₂x²+a₃x³, 则(a₀+a₂+a₄)²－(a₁+a₃)²=__________.

17、若二项式(x－)⁶的展开式中第5项是－,那么(…+)=__________.

18、=___________.(q≠－1)　(填入所有的可能值)

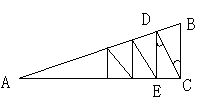19、如图，从∠BAC的边上一点B作BC⊥AC,从点

C作CD⊥AB, 从点D再作DE⊥AC,　这样无

限进行下去。设BC=7cm, CD=6cm.则这样的所

有垂线长的和为____________.

20、=_______________.

三、解答题

21、对于二项式(1－x)¹⁰

（1）展开式的中间项是第几项？写出这一项；

（2）求展开式中各二项式系数之和

（3）求展开式中除常数项外，其余各项的系数和；

（4）写出展开式中系数最大的项；

（5）当x=2002时，求(1－x)¹⁰被2除所得的余数.

22、已知数列｛a_n｝ ：a_n=++…+.

（1）求a₁₀₀的值；

（2）设b_n=，求S_n=b₁+b₂+…+b_n；

（3）求S_n.

23、平行六面体ABCD—A^/B^/C^/D^/中，底面ABCD是边长为a的正方形，侧棱AA^/长为b,且

∠A^/AB=∠A^/AD=120⁰　

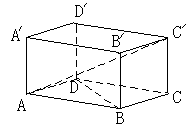（1）求值线AC^/与BD所成角；

（2）求.

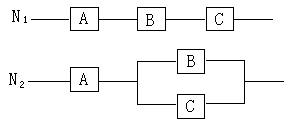
24、用A、B、C三个不同元件连接成两个系统N₁、N₂，当元件A、B、C都正常工作时，系统N₁正常工作.当元件A正常工作，且B、C至少有一个正常工作时，系统N₂正常工作.已知元件A、B、C正常工作的概率分别为0.80，0.90，0.90，分别求两个系统正常工作的概率.

参考答案

一、选择题

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	B	D	B	D	B	C	D	A	D	A	A

二、填空题

13．　 12　　 　14． 　180　　　15．　　16．　1　　　17． 　1　

18．q＜1时为1，q=1时为0，q＞1时为－1　　　 

19．　 49cm　  　　　 20．　－11　　

 三、解答题

21、（1）T₆=－252x⁵

（2）2¹⁰=1024

（3）a₀=1　　　a₁+…a₁₀=－1

（4）T₅=210x⁴　　　T₇=210x⁶

（5）(1－x)¹⁰=2002M+1　 全长为1

22、（1）a_n=　　　 a₁₀₀=50

（2）b_n=4(－)　　 S_n=4(1－)

（3）S_n=4

23、（1）·=（++）（－）=0

　　∴⊥

（2）=++²=2a²+b²－2ab

　　=

24、(1) P(ABC)=0.8×0.9×0.9=0.648

　　(2) P(B+C)=1－P(BC)=1－0.9×0.1=0.99

　　　 P[A(B+C)]=P(A)·P(B+C)=0.8×0.99=0.792