高二数学(文)上期半期考试
(一卷)
一、选择题(每小题5分,共60分)
1、若点B在直线![]() 上,
上,![]() 在平面
在平面![]() 内,则B、
内,则B、![]() 、
、![]() 之间的关系可记作( )
之间的关系可记作( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、双曲线![]() 的渐近线方程为( )
的渐近线方程为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、下列方式不一定能确定一个平面的是( )
A、两条相交直线 B、两条平行直线
C、不共线的四点 D、直线和直线外一点
4、已知点P![]() 与点Q
与点Q![]() 关于直线
关于直线![]() 对称,则直线
对称,则直线![]() 的方程为( )
的方程为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、已知点A![]() ,B
,B![]() ,动点P满足
,动点P满足![]() ,则P点轨迹为( )
,则P点轨迹为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、已知椭圆焦点在![]() 轴,中心在原点,过左焦点
轴,中心在原点,过左焦点![]() 作垂直于
作垂直于![]() 轴的弦AB,使得
轴的弦AB,使得![]() 为正三角形,则椭圆的离心率为( )
为正三角形,则椭圆的离心率为( )
 A、
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、表示图中阴影区域的不等式组为( )
A、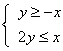 B、
B、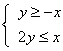
C、![]() D、
D、![]()
8、已知定点A![]() ,B
,B![]() ,在
,在![]() 轴上找一点P,则
轴上找一点P,则![]() 的最小值为( )
的最小值为( )
A、6 B、![]() C、8 D、10
C、8 D、10
9、已知抛物线![]() 的准线和双曲线
的准线和双曲线![]() 的左准线重合,则双曲线的方程为( )
的左准线重合,则双曲线的方程为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、与直线![]() 的夹角为
的夹角为![]() 的一条直线方程为( )
的一条直线方程为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、动圆![]() 圆心在直线
圆心在直线![]() 上,且和直线
上,且和直线![]() 相切点
相切点![]() ,则半径为( )
,则半径为( )
A、5 B、![]() D、
D、![]()
12、椭圆![]() 上一点P到左焦点距离与到右准线的距离相等,则P点的到
上一点P到左焦点距离与到右准线的距离相等,则P点的到![]() 轴的距离为( )
轴的距离为( )
A、4 B、![]() C、3 D、
C、3 D、![]()
(二卷)
二、填空题(每小题4分,共16分)
13、双曲线![]() 以椭圆
以椭圆![]() 的焦点为顶点,长轴的两端点为焦点,则它的方程是
。
的焦点为顶点,长轴的两端点为焦点,则它的方程是
。
14、椭圆![]() 上到直线
上到直线![]() 的最近距离为
。
的最近距离为
。
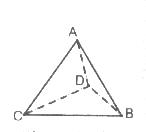 15、如图:A、B、C、D四点不共面,则线段AB、AC、AD、BD、BC、CD中异面的共有 对。
15、如图:A、B、C、D四点不共面,则线段AB、AC、AD、BD、BC、CD中异面的共有 对。
16、过抛物线![]() 上一点P
上一点P![]() ,作倾斜角互补的弦PA、PB,则AB弦的斜率为
。
,作倾斜角互补的弦PA、PB,则AB弦的斜率为
。
三、解答题(共74分)
17、(13分)求经过直线![]() 和直线
和直线![]() 的交点,且和直线
的交点,且和直线![]() 平行的直线。
平行的直线。
18、(13分)已知圆的半径为![]() ,圆心在直线
,圆心在直线![]() 上,圆被直线
上,圆被直线![]() 截得的弦长为
截得的弦长为![]() ,求圆的方程。
,求圆的方程。
19、(13分)抛物线顶点在原点,焦点在坐标轴上,抛物线在第一象限内一点P到![]() 轴得距离为6,到准线的距离为10,求抛物线方程。
轴得距离为6,到准线的距离为10,求抛物线方程。
20、(13分)双曲线的中心在原点,焦点在![]() 轴,且过点A
轴,且过点A![]() 和B
和B![]() 。
。
(1)求双曲线方程;
(2)![]() 为双曲线的左焦点,直线
为双曲线的左焦点,直线![]() 交双曲线左支于C,求
交双曲线左支于C,求![]() 。
。
21、(12分)已知椭圆![]() ,
,![]() 为椭圆的左右焦点,过右焦点
为椭圆的左右焦点,过右焦点![]() 的直线交椭圆于AB两点,求
的直线交椭圆于AB两点,求![]() 的重心轨迹。
的重心轨迹。
22、(10分)已知曲线![]() 上的动点P到直线
上的动点P到直线![]() 的距离是到点
的距离是到点![]() 的两倍。
的两倍。
(1) 求![]() 的轨迹。
的轨迹。
(2)抛物线![]() :
:![]() 的焦点与曲线
的焦点与曲线![]() 有的一个焦点F重合,过F作互相垂直的直线
有的一个焦点F重合,过F作互相垂直的直线![]() ,
,![]() ,使得
,使得![]() 交
交![]() 于点A,B,
于点A,B,![]() 交曲线
交曲线![]() 于点C,D,求四边形ABCD面积的取值范围。
于点C,D,求四边形ABCD面积的取值范围。