高二数学半期综合测试题

高二数学半期综合测试题

班级　　　　　　　 　　　 姓名　　　　　　　 

一、选择题（本大题共12小题，每小题4分，共48分）

1．已知点（2，－1）和（－3,2）在直线的异侧，则的取值范围是（　　）

　　　 A．（4,7）　　　　　　　　B．（－4,7）　　　　　　 C．（－7,4）　　　　　　 D．（－4,4）

2．在下列函数中，当x取正数时，最小值为2的是　　　　　　　　　　 　（　　）

A．y=x+　 　　　　　　　　　　　　　　　　　　　　 B．　

　　　 C．　　　　　　　 D．y=x²－2x+3

3．若不等式＞0的解为－3＜x＜－1或x＞2，则a的值为　　　（　　）

A．2　　　　  　　　B．－2 　　　　　　　　　C．　　　　　　　　　 D．－

4．若点A（4，a）到直线4x－3y－1＝0的距离不大于3，则　　　　　　　　　　　　 （　　）

　　　 A．－1＜a＜9　　　　　B．0≤a≤10　　　　　　C．5＜a＜8　　　　　　　D．－2≤a≤6

5．已知 – 1< x + y < 3，且2 < x – y < 4，则2x +3y的取值范围是　　　　 （　　）

　　　 A．（–，）　　 B．（–，） 　　 C．（–，）　　D．（–，）

6．若抛物线上横坐标为3的点到焦点的距离等于5，则等于（　　）

A．1.5　 　　　　　　　　B．2 　　　　　　　　　　C．4　　　　　　　　　　D．8

7．直线与直线互相垂直，R，则的最小值为　　　　　　　　　　　　　　　　　　　  　　　 （　　）

　　　 A．1　　 　　　　　　　 B．2 　　　　　　　　　　C．3　　　　　　　　　　 D．4

8．在相距4k米的A、B两地, 听到炮弹爆炸声的时间相差2秒, 若声速每秒k 米, 则爆炸地点P必在　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．以A，B为焦点, 短轴长为k米的椭圆上 .　　　　　　　　　　

B．以AB为直径的圆上.

C．以A，B为焦点, 实轴长为2k米的双曲线上 .

D．以A，B为顶点, 虚轴长为k米的双曲线上

9．把曲线C₁：按向量平移后得到曲线C₂，曲线C₂有一条准线为，则　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　 B．　　　　　　　　　C．3　　　　　　　　　　　 D．－3

10．圆心在抛物线上，且与轴和该抛物线的准线都相切的一个圆的方程是

（　　）

　　　 A．　 　　　　　　B．

　　C．　　　　　　　　　 D．

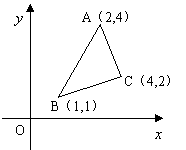
11．已知点（）在如图所示三角形及其内部运动，

如果使（）取得最大值的点（）

有无穷多个，则等于　　　　　　　　  （　　）

　　　 A．　　　　　　　　　 B．1

　　　 C．6　　　　　　　　　　　 D．3

12．若椭圆与双曲线有相同的焦点F₁、F₂，P是两曲线的一个交点，则的面积是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．4　　　 　　　　　　B．2 　　　　　　　　　C．1　　　　　　　　　　　 D．

二、填空题（本大题共4小题，第小题3分，共12分）

13．已知圆的方程为x²+y²+ax+2y+a²=0，一定点A（1，2），要使过定点A（1，2）作圆的切线有两条，则a的范围是　　　　　　　 

14．过A（1,2）、B（3,0）两点且圆心在直线y=3上的圆的方程是　　　　　　　　　　．

15．椭圆的焦点在轴上，则的取值范围是　　　　　　 ．

16．对于椭圆和双曲线有下列命题：

①椭圆的焦点恰好是双曲线的顶点;　　　　　②双曲线的焦点恰好是椭圆的顶点;

③双曲线与椭圆共焦点;　　　　　　　　　　　　　 ④椭圆与双曲线有两个顶点相同.

其中正确命题的序号是　　　　　　  .

三、解答题（本大题共4题，共40分）

17．(本小题满分10分)已知圆C：，直线：，

　 （1）求证对R，直线和圆C总相交；

　 （2）设直线和圆C交于A、B两点，当取得最大值时，求直线的方程．

18．(本小题满分10分)已知直线与圆相切于点T，且与双曲线相交于A、B两点.若T是线段AB的中点，求直线的方程.

19．(本小题满分10分)已知抛物线 y ² = – x与直线 y = k ( x + 1 )相交于A、B两点, 点O是

坐标原点.

　 （1）求证: OA^OB;　

　 （2）当△OAB的面积等于时, 求k的值.

20．(本小题满分10分)A、B、C是我军三个炮兵阵地，A在B的正东方向相距6千米，C在B的北30°西方向,相距4千米,P为敌炮阵地.某时刻,A发现敌炮阵地的某信号,由于B、C比A距P更远，因此，4秒后，B、C才同时发现这一信号（该信号的传播速度为每秒1千米）.若从A炮击敌阵地P，求炮击的方位角.

参考答案

一、选择题（本大题共12小题，每小题4分，共48分）

BDBBD　　CBCCD　　BC

二、填空题（本大题共4小题，第小题3分，共12分）

13．()　　　　　　　14． 　

 15．（2，4） 　　　　　　　　　 16. ①②

三、解答题（本大题共4题，共40分）

17．（１）证明：因圆C的圆心为C（0，1），半径，

所以圆心C到直线的距离为，命题得证。

另析：直线：恒过过定点P，可判明在圆内，即证明直线和圆C总相交。

 （2）当最小时最大，而时最小，此时的方程为．

18．直线与轴不平行，设的方程为  代入双曲线方程 整理得

　　 而，于是

　从而

即

点T在圆上　 　即　　　 ①

由圆心　.　得 　　

　则 　或

当时，由①得 的方程为 ；

当时，由①得  的方程为.故所求直线的方程为 或

19．解: (1) 当k = 0时直线与抛物线仅一个交点, 不合题意,

∴k ¹ 0由y = k (x+1)得x = –1 代入y ² = – x 整理得: y ² +y – 1 = 0 ，　

　　设A (x ₁ , y ₁), B (x ₂ , y ₂) 则y ₁ + y ₂ = –,　y ₁y ₂ = –1. 　　　　　　　　　　 

∵A、B在y ² = – x上, ∴A (–, y ₁ ), B (–, y ₂ ) ，

∴ k_OA·k_OB === – 1 .　　　　　　　　　　　

∴ OA^OB.　　　　 　　　　　　　　　　　　　　　　　　　　　　　

　　(2) 设直线与x轴交于E, 则 E ( – 1 , 0 ) ∴OE = 1 ，

S_△OAB =OE( y ₁ + y ₂ ) = y ₁ – y ₂ ==，　 解得k = ±.

20．以线段AB的中点为原点，正东方向为轴的正方向建立直角坐标系，

则 依题意　　　　

在以A、B为焦点的双曲线的右支上.这里.

其方程为

又　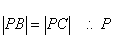又在线段AB的垂直平分线上

由方程组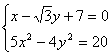　解得　 　即  

由于，可知P在北30°东方向.