高二数学单元测试——不等式(理科)
班级 姓名
一、选择题:(每小题5分,共60分,)
1.不等式![]() 和
和![]() 同时成立的充要条件是( ).
同时成立的充要条件是( ).
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.已知![]() ,且
,且![]() ,则( ).
,则( ).
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
3.下列结论正确的是( ).
(A)当![]() (B)
(B)![]()
(C)当![]() 时,
时,![]() 的最小值为2 (D)当
的最小值为2 (D)当![]() 时,
时,![]() 无最大值
无最大值
4.已知![]() ,
,![]() ,则不等式
,则不等式![]() 的解是( ).
的解是( ).
(A)![]() (B)
(B)![]()
(C)![]() ,或
,或![]() (D)
(D)![]() ,或
,或![]()
5.已知![]() ,则
,则![]() 的最小值是 ( ).
的最小值是 ( ).
(A)![]() ( B)
( B)![]() (C) 6
(D) 7
(C) 6
(D) 7
6.不等式![]() 的解集是
( )
的解集是
( )
A ![]() B.(1,5)
C.[1,+∞) D.(1,+∞)
B.(1,5)
C.[1,+∞) D.(1,+∞)
7.(2004年天津卷)不等式![]() 的解集为 (
)
的解集为 (
)
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
8.(2004年北京卷)已知a、b、c满足![]() ,且
,且![]() ,那么下列选项中不一定成立的是( )
,那么下列选项中不一定成立的是( )
A.![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.(2004年全国卷III)不等式![]() 的解集为 (
)
的解集为 (
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.(2004年全国卷IV)不等式![]() 的解集为 (
)
的解集为 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.(2005重庆卷理)若x,y是正数,则![]() 的最小值是( )
的最小值是( )
A.3 B.![]() C.4 D.
C.4 D.![]()
二.填空题:(每小题4分,共16分)
13.(2006年上海卷)不等式![]() 的解集是 .
的解集是 .
14.(2006年江苏卷)不等式![]() 的解集为
的解集为
15. 若不等式x-4+x-3>a 对一切实数恒成立,则a的取值范围为_______.
16. 若![]() ,则
,则![]() 的最小值为 .
的最小值为 .
三.解答题:(本题共74分)
17.(本题满分12分)证明下列不等式:
(1)已知![]() 都是正数,求证:
都是正数,求证:![]()
(2)已知![]() ,求证:
,求证:![]()
|
18.(本题满分12分)已知函数![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围。
的取值范围。
19.(本题满分12分)(1)求函数![]() 的值域。
的值域。
(2)已知![]() ,求
,求![]() 的最大值。
的最大值。
20.(本题满分12分)
(1)解下列不等式:![]() >x+5
>x+5
|
(2)当![]() 为何值时,不等式
为何值时,不等式![]() 对于任意实数恒成立。
对于任意实数恒成立。
21.(本题满分12分)(2005全国理)
设函数![]() ,求使
,求使![]() 的
的![]() 取值范围.
取值范围.
22.(本题满分14分)(2005江西理)
已知函数![]() (a,b为常数)且方程
(a,b为常数)且方程![]() 有两个实根为
有两个实根为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
|
参考答案
一选择题
1B,2B,3B,4D,5D,6D,
二.填空题
13.![]() ,14.
,14.![]() ,15.
,15.![]() ,16.
,16.![]() .
.
三.解答题
17.(1)
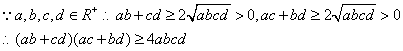
当且仅当![]() 即
即![]() 时,取“=”号.
时,取“=”号.
(2)
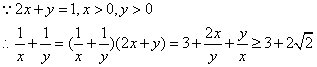
当且仅当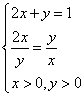 即
即![]() 时,取“=”号.
时,取“=”号.
18.![]()
设![]()
![]() 解出
解出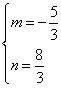
![]()
又![]()
![]() .
.
![]() ,即
,即![]()
20.
(1)
![]() 分以下两类情况讨论:
分以下两类情况讨论:
①当![]() 时,
时,![]() ,则
,则![]()
当且仅当![]() 且
且![]() ,即
,即![]() 时,取“=”号
时,取“=”号
②当![]() 时,
时,![]() ,此时
,此时![]()
![]()
当且仅当![]() 且
且![]() ,即
,即![]() 时,取“=”号
时,取“=”号
综上,![]() 的值域为
的值域为![]()
(2)
![]() 且
且![]()
![]()
![]() ,当且仅当
,当且仅当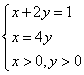 ,即
,即![]() 时,取“=”号
时,取“=”号
即![]() 的最大值为
的最大值为![]() .
.
20.
(1)原不等式同解于(Ⅰ)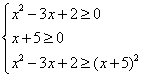 或(Ⅱ)
或(Ⅱ)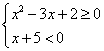
解(Ⅰ)得![]() ;解(Ⅱ)得
;解(Ⅱ)得![]() .
.
所以原不等式的解集为![]()
(2)![]() 恒大于0
恒大于0![]() 原不等式同解于
原不等式同解于![]()
即![]() .
.
由已知它对于任意实数恒成立,则有![]() ,
,
即![]() 解出
解出![]() 为所求.
为所求.
21. 解:即解
![]()
![]()
![]()
分三类 ①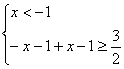
![]()
②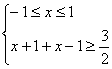
![]()
③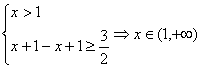
①②③求并集得 x的取值范围是[![]()
22. (1)将![]() 得
得
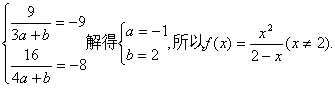
(2)不等式即为![]()
即![]()
①当![]()
②当![]()
③![]() .
.