高二数学第13周周练

高二数学第13周周练

姓名 ________　　　　　  学号____________

总分150分

一、选择题：（本大题共10个小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1，　方程表示的曲线是

A、　椭圆　　　　  B、双曲线　　　　 C、抛物线　　　　 D、不能确定

2，方程的曲线形状是

A、圆　　　　　  B、直线　　　　   C、圆或直线　　  D、圆或两射线

3，以抛物线y²=2px（p>0）的焦半径PF为直径的圆与y轴位置关系是

A、相交　　　　　 B、相切　　　　　 C、相离　　　　  D、以上三种均有可能 

4，已知＝（2，－1，3），＝（－1，4，－2），＝（7，5，λ），若、、三向量共

　 面，则实数λ等于　　　 　　　　　　　　　　　　　　　　　　 （ 　　）

A．　　　　　　　　　B．　　　　　　　　　C．　　　　　　　　　 D．

5，直三棱柱ABC—A₁B₁C₁中，若， 则 　　　　　　　（　　）

　　　 A．+－ 　　　　　B．－+ 　　　　　C．－++　　　　D．－+－

6，已知++＝，＝2，＝3，＝，则向量与之间的夹角为（ 　）

　　　 A．30°　　　　　　　　B．45°　　　 　　　 C．60°　 　　　　　　　D．以上都不对

7，已知△ABC的三个顶点为A（3，3，2），B（4，－3，7），C（0，5，1），则BC边上的

　 中线长为　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　 （　　 ）

A．2　　　　　　　　　B．3 　　　　　　　　 C．4　　　　　　　　　　 D．5

8，已知双曲线(a>0,b<0)的右焦点为F，若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点，则此双曲线离心率的取值范围是

A.( 1,2) 　　　　 B. (1,2)　　　　　 C.[2,+∞]　　　　　 D.(2,+∞)

9，已知　　　　　 （　  ）

A．－15　　　　　　　　　 B．－5　　　　　　　　　　 C．－3　　　　　　　　　　 D．－1

10，已知，，，点Q在直线OP上运动，则当

取得最小值时，点Q的坐标为　　　　　　　　　　　　　　 （　　 ）

A．　 　　　 B．　 　　　 C．　　　　　D．

题号	1	2	3	4	5	6	7	8	9	10
答案	A	D	B	D	D	C	B	C	A	C

二、填空题（本大题共4小题，每小题6分，共24分）

11．若A(m＋1，n－1,3)，B(2m,n,m－2n)，C(m＋3,n－3,9)三点共线，则m+n= 　　　 0

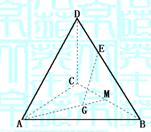
12．已知S是△ABC所在平面外一点，D是SC的中点，

若＝，则x＋y＋z＝　　　　　　 ． 0

13．在空间四边形ABCD中，AC和BD为对角线，

　　　 G为△ABC的重心，E是BD上一点，BE＝3ED，

　　　 以｛，，｝为基底，则＝　　　　　  　．

 14．设＝1，＝2，2＋与－3垂直，＝4－，

＝7＋2，　则<,>＝　　　　   0

15，高5米和3m的旗竿在水平地面上，如果把两旗竿底部的坐标分别定为A（-5，0），B（5，0），则地面上杆顶仰角相等的点的轨迹是__________。

三、解答题（本大题满分75分）

16．（12分））如图，在棱长为2的正方体ABCD－A₁B₁C₁D₁中，

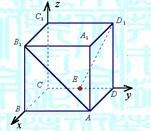
　　　 E是DC的中点，取如图所示的空间直角坐标系．

　 （1）写出A、B₁、E、D₁的坐标；

　 （2）求AB₁与D₁E所成的角的余弦值．　

解：(1) A(2, 2, 0)，B₁(2, 0, 2)，E(0, 1, 0)，D₁(0, 2, 2)

　　　　  (2)∵ ＝(0, -2, 2)，＝(0, 1, 2)　∴ ＝2，＝，·＝0－2＋4＝2,

∴ cos á，ñ ＝ ＝ ＝ ．∴ AB₁与ED₁所成的角的余弦值为．

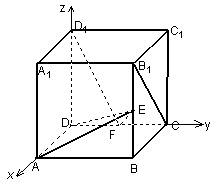
17．（12分）在正方体中， Ｅ、Ｆ分别是

 ，ＣＤ的中点，

　 （1）求证：平面ADE；

　 （2）求．

　　　

解：建立如图所示的直角坐标系，（1）不妨设正方体的棱长为1，

则D（0，0，0），A（1，0，0），（0，0，1），

　　　　 E（1，1，），F（0，，0），

　　　　 则＝（0，，－1），＝（1，0，0），　　

　　　　 ＝（0，1，），  则＝0，

　　　　 ＝0， ，.　　

　　　　 平面ADE.

（２）（1，1，1），C（0，1，0），故＝（1，0，1），＝（－1，－，－），

　　　　 ＝－1＋0－＝－，　　 ，，　　

则cos. .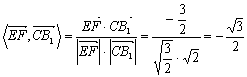　　　　

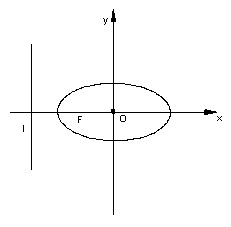18，（本小题满分12分）　　已知椭圆的左焦点为F，O为坐标原点。

　　　 （I）求过点O、F，并且与椭圆的左准线相切的圆的方程；

　　　 （II）设过点F的直线交椭圆于A、B两点，并且线段AB的

　　　　　　　中点在直线上，求直线AB的方程。

 

 

 

　

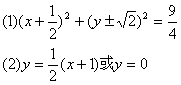
19，设双曲线上两点A、B，AB中点M（1，2）

（1）求直线AB方程；

　 （2）如果线段AB的垂直平分线与双曲线交于C、D两点，那么A、B、C、D是否共圆，为什么？

（1）显然AB斜率存在

 设AB：y-2=k(x-1)

 由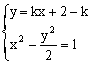得：(2-k²)x²-2k(2-k)x-k²+4k-6=0

 当△>0时，设A（x₁,y₁），B（x₂,y₂）

 则

 ∴ k=1，满足△>0

 ∴ 直线AB：y=x+1

 法二：设A（x₁,y₁），B（x₂,y₂）

 则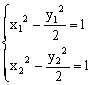

 两式相减得：(x₁-x₂)(x₁+x₂)=(y₁-y₂)(y₁+y₂)

 ∵ x₁≠x₂

 ∴

 ∴

 ∴ AB：y=x+1

 代入得：△>0

　　 

设A、B、C、D共圆于⊙OM，因AB为弦，故M在AB垂直平分线即CD上；又CD为弦，故圆心M为CD中点。因此只需证CD中点M满足MA=MB=MC=MD

由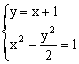得：A（-1，0），B（3，4）

又CD方程：y=-x+3

由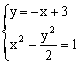得：x²+6x-11=0

设C（x₃,y₃），D（x₄,y₄），CD中点M（x₀,y₀）

则

∴ M（-3，6）

∴ MC=MD=CD=

又MA=MB=

∴ MA=MB=MC=MD

∴ A、B、C、D在以CD中点，M（-3，6）为圆心，为半径的圆上

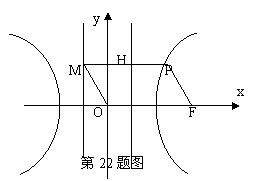
 20，（本大题满分14分）如图，F为双曲线C：的右焦点。P为双曲线C右支上一点，且位于轴上方，M为左准线上一点，为坐标原点。已知四边形为平行四边形，。

（Ⅰ）写出双曲线C的离心率与的关系式；

（Ⅱ）当时，经过焦点F且平行于OP的直线交双曲线于A、B点，若，求此时的双曲线方程。

 

解：∵四边形是，∴，作双曲线的右准线交PM于H，则，又，。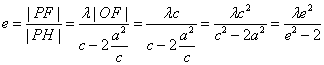

（Ⅱ）