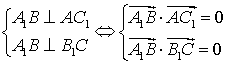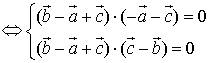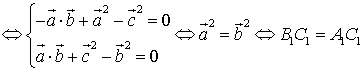高二数学第二次月考试题

高二数学第二次月考试题

命题人：罗小青　2006。12。27

一、选择题（本大题共12小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的）

1．经过空间任意三点作平面　　　　　　　　　　　　　　　　　  　　　　　　　　　 （　　）

　　　 A．只有一个　　　　　　　　　　　　　　　　　　　　　 B．可作两个 　　　　　

　　　 C．可作无数多个　　　　　　　　　　　　　　　　　　D．只有一个或有无数多个

2．若＝（2，1，1）， =（﹣１，x，1）且⊥　，则x的值为　　 　　　　　　（　　）

　　　 A．1　　　　　　　　　　B．－1　　　　　　　　　C．2　　　 　　　　　　D．0

3. 设向量是空间一个基底，则一定可以与向量构成

　　　 空间的另一个基底的向量是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　 B．　　　　　　　　　　 C．　　　　　　　　D．

4．已知α，β是平面，m，n是直线.下列命题中不正确的是　　　　　　　　　  （　　）

　　　A．若m∥n，m⊥α，则n⊥α　　　　　　　 B．若m∥α，α∩β=n，则m∥n

　　　 C．若m⊥α，m⊥β，则α∥β　　　　　　 D．若m⊥α，，则α⊥β

5．三棱柱ABC—A₁B₁C₁中，若　　　　　　　　　(　　)

C1

A

C

A．　　　　　　 

B

B．　　　

A1

C．

B1

D．

6．设M、O、A、B、C是空间的点，则使M、A、B、C一定共面的等式是（　 ）

A．　　　　 B．

C．　　  D．

7．三棱锥ABCD中， ，，，则△BCD是　　 （　　）　　　　　　　　　　　　　　　　　　　　　　　　  A．钝角三角形　　　B．直角三角形　　　C．锐角三角形　　 D．不确定

8．两个完全相同的长方体的长、宽、高分别为5cm，4cm，3cm，把它们重叠在一起组成一

　 个新长方体，在这些新长方体中，最长的对角线的长度是　　　　  　　　　　　　　　 （　　）

　　　 A．　　　　　　　B．　　　　　　　C．　　　　　　　D．

9.已知(　　 )

　　　 A．　　　 B．5，2　　　　　　　　 C．　　　　　 D．-5，-2

10.已知二面角的平面角是锐角，内一点到的距离为3，点C到棱的距离为4，那么的值等于　 　　　　　　　　　　　　　　(　　 )

A、　　　　　　　　　　B、　　　　　　　　　　 C、　　　　　　　　　D、

11．正方形ABCD的边长为6 cm，点E在AD上，且AE＝AD，点F在BC上，且BF ＝BC，

　把正方形沿对角线BD折成直二面角A－BD－C后，则EF ＝　　　　　　　　　　　　　（　　 ）

　　　 A．2cm 　　　　　　B．2cm　　　　　 C． 2cm　　　　　　D．6 cm

12．在下列的四个命题中：

①是异面直线，则过分别存在平面，使；

②是异面直线，则过分别存在平面，使；

③是异面直线，若直线与都相交，则也是异面直线；

④是异面直线，则存在平面过且与垂直．真命题的个数为　　　　　　　（　　）

　　　 A．1个　　　　　　　　　　B．2个　　　　　　　　　 C．3个　　　　　　　　 D．4个

二、填空题（本大题共4小题，每小题4分，共16分）

13．正方体中，平面和平面的位置关系为　　　　　 

14．若A(m+1,n-1,3),B(2m,n,m-2n),c(m+3,n-3,9)三点共线，则m+n= 　　　　　　　　　  .

15．已知A（0，2，3），B（-2，1，6），C（1，-1，5），若的坐标为 　　　　　　　　　  .

16．将边长为2，锐角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD，点E、F分别为AC、BD的中点，则下列命题中正确的是　　　　　　 。（将正确的命题序号全填上）

　　①EF∥AB　　　　　　　　　　　　　　　 ②EF是异面直线AC与BD的公垂线

③当四面体ABCD的体积最大时，AC=　④AC垂直于截面BDE

三、解答题（本大题共6题，共56分）

17．(8分)已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点，且ＥＨ∥ＦＧ．求证：EH∥BD.　

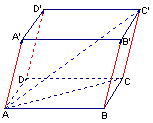18．(8分) 已知平行六面体中，

，

，求的长

19．（10分）如图，三棱柱ABC—A₁B₁C₁中，、B₁B、C₁C垂直底面，底面△ABC中，CA=CB=1，∠BCA=90°，棱AA₁=2，M、N分别是A₁B₁，A₁A的中点，

　　　 （1）求

　　　 （2）异面直线

　　　 （3）

20．（１0分）

（文科做）求证：空间四边形的两条对角线是异面直线。

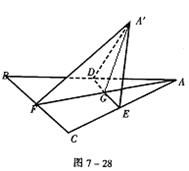
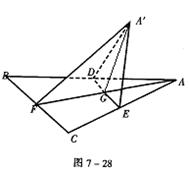
（理科做）已知边长为a的正三角形ABC的中线AF与中位线DE相交于G（如图7-28），将此三角形沿DE折成二面角A′—DE—B。（1）．求证：平面A′GF⊥平面BCED；（2）．当二面角A′—DE—B为多大时，异面直线A′E与BD互相垂直？证明你的结论。

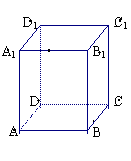
21．（10分）长方体ABCD-A₁B₁C₁D₁中AB=BC=，AA₁=3，点E，F分别在BB₁，DD₁上，且AE⊥A₁B，AF⊥A₁D．

①求证：A₁C⊥面AEF；　　②求二面角A-EF-B的大小；③点B₁到面AEF的距离；_下

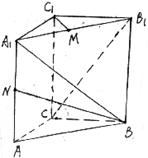
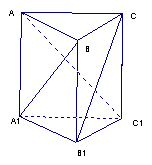
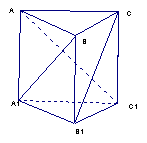
22．（１0分）如图, 已知三棱柱ABC—A₁B₁C₁中，、B₁B、C₁C垂直底面，有下列三个条件：（1）, (2 )  (3)  , 问利用 （1），（2），（3）可以构造出多少个正确的命题，请写出这些正确的命题,并选择其中一个正确命题加以证明。

　　　　　　　　　　　　　　　　　　　　　　　　

高二数学第三次月考试题参考答案

一、选择题（本大题共12小题，每小题4分，共48分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	A	C	B	D	D	C	C	A	D	A	B

二、填空题（本大题共4小题，每小题4分，共16分）

13．平行　　　 14．0　　　　15．(1,　1,　1,) 或 (-1 , -1,　-1) 　　　16．②③④

三、解答题（本大题共6题，共56分）

17（8分）证明：面，面

面　　　　　　　　　　　　　　　　　　 

　　　又面，面面，

　　　　　　　　　　　　　　　　　　　

18、（8分）解：

 

所以，．　　　　　　

19．（10分） 解：（1）以射线建立坐标系，则B（0，1，0）

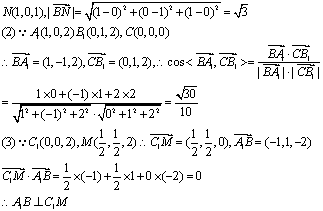
20、（10分）文科用反证法

理科解　（1）∵△ABC是正三角形，AF是BC边的中线，

∴AF⊥BC。

又D、E分别是AB、AC的中点，

∴DE∥BC。

∴AF⊥DE，又AF∩DE=G，　　　∴A′G⊥DE，GF⊥DE，

∴DE⊥平面A′FG，　　　　　　又DE平面BCED，

∴平面A′FG⊥平面BCED。

（2）∵A′G⊥DE，GF⊥DE，

∴∠A′GF是二面角A′—DE—B的平面角。

∵平面A′GF∩平面BCED=AF，

作A′H⊥AG于H ，　　　∴A′H⊥平面BCED。

假设A′E⊥BD，连EH并延长AD于Q，则EQ⊥AD。

∵AG⊥DE，

∴H是正三角形ADE的重心，也是中心。

∵AD=DE=AE=，∴A′G=AG=a,　　HG=AG=a。

在Rt△A′HG中，cos∠A′GH==.

∵∠A′GF =π-∠A′GH, 　　　　　　　　　∴cos∠A′GF= -，

∴∠A′GF=arccos(-)，

即当∠A′GF=－arccos时，A′E⊥BD。

21．（10分）解：①∵BC⊥面AA₁B₁B　∴A₁B那么A₁C在平面AA₁B₁B上的射影

又AE⊥A₁B　　AE面AA₁B₁B　 ∴AE⊥A₁C(三垂线定理)

同理：AF⊥A₁D　　又AE，AF面AEF且AE∩AF=A　∴A₁C⊥面AEF

②连AC，BD交于点O，取EF的中点M连OM，AM已知AE=AF=2

BE=DF=1　 ∠OMA即为二面角A—EF—B的平面角

在tan∠AMO=　∴∠AMO=arc tan

③　∴d=

22、（10分）解：可以构造出３个正确的命题：在直三棱柱ABC-中，

　　１：如果　且　　则　

　　２：如果　且　　则　　

　　３：如果且　　则　

最好用向量法来证．如证命题１：

　　证明：设