高二数学第一学期期末试卷
总分150分
一、填充题:
1.若直线![]() :
:![]() 与直线
与直线![]() :
:![]() 平行但不重合,
平行但不重合,
则![]() =
。
=
。
2.
已知直线![]() :
:![]()
![]() ,直线
,直线![]() 过点P (
过点P (![]() ),且
),且![]() 与
与![]() 夹角为
夹角为![]() ,则直线
,则直线![]() 的方程是
。
的方程是
。
3.已知点(![]() )(
)(![]() >0)到直线L:
>0)到直线L:![]() 的距离为1,则
的距离为1,则![]() = 。
= 。
4.若直线![]() 与两坐标轴交点为A.B,则以线段AB为直径的圆的方程是
。
与两坐标轴交点为A.B,则以线段AB为直径的圆的方程是
。
5.椭圆![]() 的右焦点坐标为
。
的右焦点坐标为
。
6.与双曲线![]() 有共同渐近线,且过点
有共同渐近线,且过点![]() 的双曲线方程是
。
的双曲线方程是
。
7.若方程![]() 表示的曲线是椭圆,则
表示的曲线是椭圆,则![]() 的取值范围是
。
的取值范围是
。
8.设抛物线![]() 的准线与直线
的准线与直线![]() 的距离为3,则抛物线方程为
。
的距离为3,则抛物线方程为
。
9.已知![]() 且
且![]() ,则P点的轨迹方程是
。
,则P点的轨迹方程是
。
10.将一张坐标纸折叠一次,使得点![]() 与
与![]() 重合,且点
重合,且点![]() 与
与![]() 重合,则
重合,则![]() 。
。
11若直线![]() 与曲线
与曲线![]() 恰有一个公共点,则
恰有一个公共点,则![]() 的取值范围是
。
的取值范围是
。
12.直线![]() 与曲线
与曲线![]() 只有一个公共点,则
只有一个公共点,则![]() 值为
。
值为
。
二、选择题:
13.已知直线![]() 与圆
与圆![]() 相切,则三条边长分别为
相切,则三条边长分别为![]() 的三角形是
。
的三角形是
。
(A)锐角三角形 (B)直角三角形 (C)钝角三角形 (D)不存在
14.动圆与圆![]() 和
和![]() 都外切,则动圆圆心的轨迹是
。
都外切,则动圆圆心的轨迹是
。
(A)抛物线 (B)圆 (C)双曲线的一支 (D)椭圆
15.若![]() ,则直线
,则直线![]() 的倾斜角的取值范围是
。
的倾斜角的取值范围是
。
(A) ![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D) ![]()
16.若点![]() 在直线
在直线![]() 运动,则
运动,则![]() 的最小值为
。
的最小值为
。
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D) 13
(D) 13
三、解答题:
17.已知点![]() 和圆C:
和圆C:![]() ,求一束光线从点A出发,经过X轴反射到圆周C的最短路程。
,求一束光线从点A出发,经过X轴反射到圆周C的最短路程。
18.设![]() 是椭圆
是椭圆![]() 的两个焦点,P为椭圆上的一点,已知P.,
的两个焦点,P为椭圆上的一点,已知P.,![]() 是一个直角三角形的三个顶点,且
是一个直角三角形的三个顶点,且![]() ,求
,求![]() 得值。
得值。
19.证明:过抛物线的焦点作一直线与抛物线交于A,B两点,则当AB与抛物线的对称轴垂直时,AB的长度最短。
20.已知对任意平面向量![]() ,把向量
,把向量![]() 绕其起点沿逆时针方向旋转得到向量
绕其起点沿逆时针方向旋转得到向量![]() ,叫做把点B绕点A沿逆时针方向旋转
,叫做把点B绕点A沿逆时针方向旋转![]() 角得到点P。
角得到点P。
⑴已知平面上点A(1,2),点B(![]() ),把点B绕点A沿顺时针方向旋转
),把点B绕点A沿顺时针方向旋转![]() 角后得到点P,求点P的坐标。
角后得到点P,求点P的坐标。
⑵设平面上的曲线C上的每一点绕坐标原点沿逆时针方向旋转![]() 角后得到点的轨迹是双曲线
角后得到点的轨迹是双曲线![]() ,求原来曲线C的方程。
,求原来曲线C的方程。
![]()
![]() 高二数学第一学期期末试卷
高二数学第一学期期末试卷
答题纸
一、填充题:(每小题4分,共48分)
1. 2. 3. 4.
5. 6. 7. 8.
9. 10. 11. 12.
二、选择题:(每小题4分,共16分)
13. 14. 15. 16.
三、解答题:
17.题(6分)
解:
18.题(8分)
解:
19.题(10分)
解:
20.题(12分)
解:
答案
一、填充题:
1.![]() 2.
2.![]() or
or ![]() 3.
3.![]() 4.
4.![]() 5.
5.![]() 6.
6.![]()
7.![]() 8.
8.![]() or
or ![]() 9.
9.![]()
10.![]() 11.
11.![]() 12.
12.![]() or
or ![]() or
or ![]()
二、选择题:
13.B 14.C 15.B 16.D
三、解答题:
17.解:圆C:![]()
点A关于X轴的对称点![]()
![]() ,则A到圆C的最短路程为
,则A到圆C的最短路程为![]()
![]()
![]() Y
Y
 A
A
![]()
![]()
![]()
![]()
X
![]()
18.解:设![]()
![]()
![]()
若![]() 则
则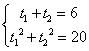
![]()
![]()
![]()
若![]() 可得
可得![]() ,
,![]() 则
则![]()
19.证明:设抛物线L的方程是![]()
焦点为![]() ,则当AB与L的对称轴垂直时,
,则当AB与L的对称轴垂直时,![]()
当AB与L对称轴不垂直时,设其方程为![]()
则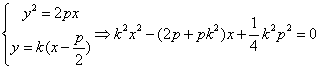
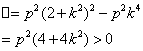
![]()
![]()
![]() 当AB与抛物线的对称轴垂直时,AB的长度最小
当AB与抛物线的对称轴垂直时,AB的长度最小
20.解:⑴![]()
![]() 是由
是由![]() 绕起点A沿逆时针方向旋转
绕起点A沿逆时针方向旋转![]() 角得到
角得到
![]()
![]()
![]() 点P的坐标
点P的坐标![]()
⑵设点![]() ,点
,点![]() 绕坐标原点逆时针方向旋转
绕坐标原点逆时针方向旋转![]() 角后得到点
角后得到点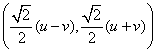 该点在双曲线
该点在双曲线![]() 上
上
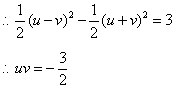
则曲线C方程是![]()