高二第一学期期中考试数学试卷

高二第一学期期中考试数学试卷

注意事项：

1、 本试卷分第一卷（选择题）和第二卷（非选择题）两部分．全卷共22个题，满分 分，考试时间分钟．

2、  答第一卷前，考生务必将自己的姓名、考生号、考试科目用铅笔涂写在机读卡上．

3、  每小题选出答案后，用铅笔把机读卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上

4、考试结束，监考人员将本试卷第二卷和机读卡一并收回．

第一卷（选择题，共60分）

一、选择题：共12个小题，每小题5分，共60分。

1、若，则下列不等式中成立的是：

A．　 B. 　 C. 　 D.

2、直线的倾斜角为：

A．150°　　　　　　 B. 120°　　　　　　 C. 60°　　　　　D. -60°

3、直线，互相垂直，则的值为（　）

A．-3　　　　　　　　B.  1　　　　　　　　C. 1或3　　　　 D. 1或-3

4、过点A(1，-1)，B(-1，1)且圆心在直线x+y-2=0上的圆方程为：

A. (x-1)² +(y-1)²=4　　　 B. (x+3)²+(y-1)²=4　　C. (x-3)²+(y+1)²=4　　　 D. (x+1)²+(y+1)²=4

5、由点P（－1，4）向圆引的切线长是：　　　　　　　　　

A．3　　　　　　　　　　　　　　 B．6　　　　　　　　　　　　　　　C．10　　　　　 D．5

6、用一段长为9的篱笆围成一个一边靠墙的矩形菜园，菜园的最大面积为：

A．9　　　　　　　  B.　 　　　　　　  C.　　　　　 D. 12

7、关于x的不等式│x-3│+│x+3│≥恒成立，实数a的最大值是：

A．6　　　 　　　　　　 B．7 　 　　　　　　　 C．1 　　　　  D．8

8、方程表示双曲线，则有：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

A．　　　　　　　　　B．　　　　　　　　C．　　　　　　　D．

9、圆 与圆 的位置关系是：

A.内切　　　　　　　  B.外切　　　　　  C.相离　　　　　  D.内含

10、某厂生产甲、乙两种产品，产量分别为45个、50个，所用原料为A、B两种规格的金属板，每张面积分别为2m²、3m²，A种金属板可造甲产品3个，乙产品5个，用B种金属板可造甲、乙产品各6个，则A、B两种金属板各取多少张，能完成计划并能使总用料面积最省？

A．A用2张，B用6张　　　　　　　　　　　　　　B．A用4张，B用5张

C．A用3张，B用5张　　　　　　　　　　　　　D．A用3张，B用6张

11、以双曲线的实轴、虚轴分别作为虚轴、实轴，所得的双曲线方程为：

A. 　　　　B. 　　　C. 　　 D.

12、椭圆的半焦距为c，点P（c，2c）在椭圆上，则椭圆的离心率为：A．　　B．　　　　　　　　　　　　　　　　　　　 C．　　　　　　　 D．

二、填空题：共4小题，每小题4分，共16分。

13. 不等式的解集是__________

14. 椭圆的一个焦点是F(0，2)，则等于　　　　　 

15. 圆心都在直线上的两圆交于点A、B，若A(4，5)，则点B坐标是　　

16. 双曲线上点P到左焦点距离是10，点P到右焦点的距离是　　　

填空题答案填入后面答题卷对应题号后的横线上

学校　　　　　　　  　　班级　　　　　 　 姓名　　　　　　 　准考证号

密　　封　　线　　 内　　不　　要　　答　　题　　　　 密　　封　　线　　 内　　不　　要　　答　　题

高二第一学期期中考试数学试卷答 题 卷

第二卷（非选择题，共90分）

二、填空题（每小题4分，共16分）

 

13、　　　　　　　　  14、　　  15、　　　 16、　　

三、解答题：（共6小题，共74分。）

17、（本题满分12分）求长、短轴之比为，一个焦点是(0,-2)，中心在原点的椭圆离心率和椭圆方程．

18、（本题满分12分）点A(4，-3)和B(2，3)到直线l的距离都等于3，求直线l的方程。

19、（本题满分12分）动点M到直线的距离与到点A(1，0)的距离之比为。　　　　  　　　　　　　　

 (1)求动点M的轨迹曲线C的方程。　　　　　　　　　　　

(2)若(1)中的曲线C的一条弦PQ以点B(-3，1)为中点，求直线PQ方程。

20、（本题满分12分）对称轴为两坐标轴且过点P的双曲线渐近线方程为

（1）求双曲线方程；

（2）F₁和F₂是双曲线的左、右焦点，点P在双曲线上，且PF₁·PF₂=32，求∠F₁PF₂的大小.

　　　　

　

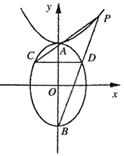
21、（本题满分12分）点A、B分别是椭圆的上、下两顶点，P是双曲线上在第一象限内的一点，直线PA、PB分别交椭圆于C、D点，如果D恰是PB 的中点，（1）求点P坐标；（2）求直线CD的斜率。

　

　　　　　　　　　　　　　　　　　　　　　　　　　 

　 　　　　　　　　　　　　　　　　　　　　　　　　　

22、（本题满分14分）椭圆＞＞的一个焦点为(1，0)，椭圆与直线交于M、N两点，以MN为直径的圆经过坐标原点O. 求线段MN的长。

　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

高二第一学期期中考试数学试卷参考答案

一、选择题：CBDDA　BBDBD　 CC

二、填空题：13. {x│x>-2且x≠1} 　 14.  1 　 15.  (5，4) 　16.  18 　

三、解答题：

17．解：由已知得： ，故，………4分

，………7分…………10分

故椭圆的标准方程为　………………12分

18、解：当直线l与直线AB平行时，设直线l方程为：3x+y+m=0　　…2分

由，得，直线l方程…6分

当直线l过线段AB中点(3,0)时，设l方程为：　　　　  …8分

由，得或直线l方程为y=0或3x-4y-9=0　 …12分

19. 解(1)设M(x,y)有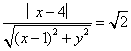 …2分，故M轨迹方程：x²+4x+2y²-14=0…6分

(2)设P(x₁,y₁)，Q(x₂,y₂),由x₁²+4x₁+2y₁²-14=0 ，x₂²+4x₂+2y₂²-14=0

得(x₁-x₂)(x₁+x₂+4)+2(y₁-y₂)(y₁+y₂)=0……8分　 又x₁+x₂=-6，y₁+y₂=2

∴………10分 ∴直线PQ方程为x-2y+5=0……12分

20. 解（1）设双曲线方程……3分 ……5分

∴双曲线方程为…………6分

（2）设PF₁=d₁，PF₂=d₂，则d₁·d₂=32，又d₁－d₂=2a=6…………8分

　即有………………10分

又F₁F₂=2c=10　 ……12分

21．解：（1）设P点坐标为，又A、B坐标分别是、

而D是PB的中点，∴D点坐标为，……………………2分

把D点坐标代入椭圆方程得： ① 又 ②

故舍去）……5分 ∴ 点坐标为………6分

（2），直线PA的方程是……………8分

由联立，解得C点坐标为……10分

又D点坐标为∴直线CD的斜率等于0。……………12分

22、解: （1）由和得…3分

=……4分

设……6分

以MN为直径的圆过原点，故OM ⊥ ON  x ₁ x ₂ + y ₁ y ₂ = 0  ……7分

　∴ …9分

又

……11分

∴MN=

　　 ……14分

对于考生的不同于参考答案的正确解答应参照各步骤得分标准给分。