高二级第一次月考数学试卷(必修五)
姓名 班别 登分号 成绩
一、选择题:(每小题5分,共50分)
1、ΔABC中,a=1,b=![]() , ∠A=30°,则∠B等于 (
B )
, ∠A=30°,则∠B等于 (
B )
A.60° B.60°或120° C.30°或150° D.120°
2、符合下列条件的三角形有且只有一个的是 ( D )
A.a=1,b=2 ,c=3
B.a=1,b=![]() ,∠A=30°
,∠A=30°
C.a=1,b=2,∠A=100° D.b=c=1, ∠B=45°
3、两灯塔A,B与海洋观察站C的距离都等于a(km), 灯塔A在C北偏东30°,B在C南偏东60°,则A,B之间的相距 ( C )
A.a
(km) B.![]() a(km)
C.
a(km)
C.![]() a(km)
D.2a (km)
a(km)
D.2a (km)
![]() 4、数列
的一个通项公式是
( D )
4、数列
的一个通项公式是
( D )
![]()
![]()
A. B.
C. D.
5、等差数列{an}中,已知a1=![]() ,a2+a5=4,an=33,则n为
( A )
,a2+a5=4,an=33,则n为
( A )
A.50 B.49 C.48 D.47
6、已知等比数列{a n }的公比为2, 前4项的和是1, 则前8项的和为 ( B )
A .15. B.17. C.19. D .21
![]() 7、已知-9,a1,a2,-1四个实数成等差数列,-9,b1,b2,b3,-1五个实数成等比数列,则b2(a2-a1)=
( B )
7、已知-9,a1,a2,-1四个实数成等差数列,-9,b1,b2,b3,-1五个实数成等比数列,则b2(a2-a1)=
( B )
A.8
B.
8、等差数列{an}中,a1+a2+…+a50=200,a51+a52+…+a100=2700,则a1等于( C )
A.-1221 B.-21.5 C.-20.5 D.-20
9、某企业在2000年和2001年两年中, 若月产值的增长率相同, 均为p, 那么这两年间年产值的增长率为 ( D )
A.(1 + p )12 %. B .[( 1 + p )12 – 1 ]% C. ( 1 + p )11 – 1 . D. ( 1 + p )12 – 1 .
10、设 {a n }是由正数组成的等比数列, 且公比q = 2, 如果a 1 · a 2 · a 3 · … · a 30 = 230, 那么a 3 · a 6 · a 9 · … · a 30 = ( C )
A.210. B.215. C.220. D.216.
二、填空题:(每小题5分,共20分)
11、在△ABC中,sinA=2cosBsinC,则三角形为 ![]() (等腰)
(等腰)
12、数列 1![]() , 2
, 2![]() , 3
, 3![]() , 4
, 4![]() , 5
, 5![]() , …, n
, …, n![]() , 的前n项之和等于
, 的前n项之和等于
13、已知数列{ a n }满足条件a1
= –2 , a n + 1 =2 + ![]() , 则a 5 =
, 则a 5 = ![]() .
.
14、已知数列{an}中,a1=3,对任意自然数n都有![]() = n(n+1),则数列{an}的通项为_________________.
= n(n+1),则数列{an}的通项为_________________.
二、解答题:
15、在△ABC中,已知![]() ,
,![]() ,B=45° 求A、C及c (14分)
,B=45° 求A、C及c (14分)
解一:由正弦定理得:![]()
∵B=45°<90° 即b<a ∴A=60°或120°
当A=60°时C=75° ![]()
当A=120°时C=15° ![]()
解二:设c=x由余弦定理 ![]()
将已知条件代入,整理:![]()
解之:![]()
当![]() 时
时
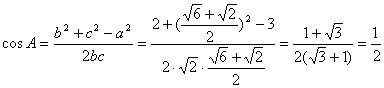
从而A=60° ,C=75°
当![]() 时同理可求得:A=120° ,C=15°
时同理可求得:A=120° ,C=15°
16、三个数成等比数列,其积为512,如果第一个数与第三个数各减2,则成等差数列.
求这三个数. (12分)
解:设三数为![]()
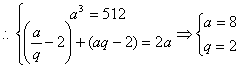 或
或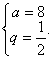
则三数为![]()
![]()
![]() 或
或![]()
![]() ,
,![]()
17、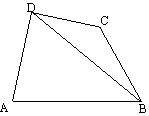 如图,在四边形ABCD中,已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长 (14分)
如图,在四边形ABCD中,已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长 (14分)
解:在△ABD中,设BD=x
则![]()
即![]()
整理得:![]()
解之:![]()
![]() (舍去)
(舍去)
由余弦定理:
![]() ∴
∴![]()
18、若数列{a n }的前n项和为S n = an2 + bn + c . 求证:数列 {a n }为等差数列的充要条件是 c = 0. (12分)
19、在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南
![]() 方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时? (14分)
方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时? (14分)
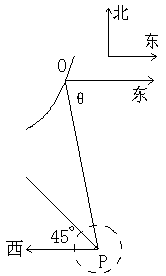
解:设经过t小时台风中心移动到Q点时,台风边沿恰经过O城,
由题意可得:OP=300,PQ=20t,OQ=r(t)=60+10t
因为![]() ,α=θ-45°,所以
,α=θ-45°,所以![]() ,
,![]()
由余弦定理可得:OQ2=OP2+PQ2-2·OP·PQ·![]()
即 (60+10t)2=3002+(20t)2-2·300·20t·![]()
即![]() ,
,
解得![]() ,
,![]()
![]()
![]()
答:12小时后该城市开始受到台风气侵袭,受到台风的侵袭的时间有12小时?
20、设![]() 数列
数列![]() 满足:
满足:![]()
![]()
(1) 求证数列![]() 是等比数列(要指出首项与公比),
是等比数列(要指出首项与公比),
(2) (2)求数列![]() 的通项公式. (14分)
的通项公式. (14分)
解:(1)![]()
![]() 又
又![]() ,
,
![]() 数列
数列![]() 是首项为4,公比为2的等比数列.
是首项为4,公比为2的等比数列.
(2)![]() .
.
![]()
令![]() 叠加得
叠加得![]() ,
,
![]()
![]()