高二级第一学期第三次考试数学试题(理科)
(总分：150分 时间；120分钟)
一、选择题：(本大题共10小题，每小题5分，共50分。在每小题列出的四个选项中，选出符合题目要求的一项。)
1、设集合
，
，
，则
=（ ）
A、
B、
C、
D、
2、在等比数列
中，
，则公比q的值为 （ ）
A、25 B、
3、方程
的两个根可分别作为（ ）
Ａ、一椭圆和一双曲线的离心率 Ｂ、两抛物线的离心率
Ｃ、一椭圆和一抛物线的离心率 Ｄ、两椭圆的离心率
4、以点（2，－1）为圆心且与直线
相切的圆的方程为（ ）
A、
B、
C、
D、
5、函数
的最小值是（ ）
A、
B、 
D、不存在
6、直线
与抛物线
交于
两点，过两点向抛物线的准线作垂线，垂足分别为
，则梯形
的面积为（ ）
A、48
B、
7、设a = 
,b = 
,c = 
，那么a,b,c的大小关系是（
）
A、a>b>c B、b>a>c C、a>c>b D、b>c>a
8、若抛物线
的焦点与椭圆
的右焦点重合，则p的值为（ ）
A、
B、
C、
D、
9、直线y ＝m(m为常数)与正切曲线y
＝
(
＞0)相交，则相邻两个交点的距离是（ ）
A、
B、
C、
D、
10、已知点F1、F2分别是双曲线
的左、右焦点，过F1且垂直于x轴的直线与双曲线交于A、B两点，若△ABF2为锐角三角形，则该双曲线的离心率e的范围是（ ）
A、
B、
C、
D、
二、填空题：(本大题共6小题，每小题4分，共24分。把答案填在题中横线上。)
11、不等式
的解集是 _____。
12、直线
的倾斜角的范围是_____________。
13、动点P与定点A（- 1，0），B（1，0）的连线的斜率之积为 -1，则点P的轨迹方程是___________。
14、已知双曲线
的右焦点为F，点A（9，2），M是双曲线上一点，则
的最小值为_____________。
15、圆
上的点到直线
的最大距离是_______________。
16、对于函数f(x)定义域中任意的x1，x2（x1≠x2），有如下结论：
①f(x1＋x2) = f(x1)·f(x2)； ② f(x1·x2) = f(x1)+f(x2) ;
③
> 0； ④
。
当f(x) = lgx时，上述结论中正确结论的序号是 。
三、解答题：(本大题共6小题，共76分。解答应写出文字说明，证明过程或演算步骤。)
17、(本题12分) 已知直线方程是
，直线方程是
。
1）求
与
的交点P的坐标；（5分）
2）求经过点P且在两坐标轴上截距的绝对值相等的直线方程。（7分）
18、(本题13分) 已知三点P（5，2）、
（－6，0）、
（6，0）.
1）求以、为焦点且过点P的椭圆的标准方程；（6分）
2）设点P、、关于直线y＝x的对称点分别为
、
、
，求以、为焦点且过点的双曲线的标准方程及渐近线方程。（7分）
19、(本题13分) 已知抛物线
的焦点为F，A、B、C三点均在抛物线上，如果
的重心与F重合，且A的纵坐标为8，求：
1）、BC边中点D的坐标；（6分）
2）、BC边所在直线的方程。（7分）
20、(本题13分) 已知p：方程
有两个不相等的负实根。已知q：方程
无实根。
1）、若p为真，求实数m的取值范围。（5分）
2）、若p或q为真，p且q为假，求实数m的取值范围。（8分）
21、(本题13分) 关于x的不等式
----（*）
1)、若a = 2，试解（*）不等式；（7分）
2）、若（*）不等式的正整数解只有x = 1，试确定实数a的取值范围。（6分）
22、(本题12分)椭圆
的两个焦点F1、F2，点P在椭圆C上，且PF1⊥PF2,,PF1=
,,PF2=
.
1）求椭圆C的方程；（5分）
2）若直线L过圆x2+y2+4x-2y=0的圆心Q交椭圆于A、B两点，且A、B关于点Q对称，求直线L的方程；（4分）
3）若2)中的线段AB的中垂线交椭圆C于M、N两点 ，则弦MN的长 = ______。（3分）
高二级第一学期第三次考试数学试题(理科)
参考答案
一、选择题：
1、D 2、D 3、A 4、C 5、D 6、A 7、C 8、B 9、B 10、B
二、填空题：
11、
12、
13、
14、
15、
16、②③
三、解答题：
17、题解：（略）
18、题解：（1）由题意可设所求椭圆的标准方程为
(a>b>0),其半焦距c=6
∴
,b2=a2-c2=9.
所以所求椭圆的标准方程为
（2）点P(5,2)、F1(-6,0)、F2(6,0)关于直线y=x的对称点分别为点P，(2，5)、F1，(0，-6)、F2，(0，6).
设所求双曲线的标准方程为
由题意知，半焦距c1=6
,b12=c12-a12=36-20=16. 所以所求双曲线的标准方程为
渐近线方程为:
.
19、题解：1）由已知得A（2，8），焦点F（8，0）。设B（
），C（
），D（
）
则：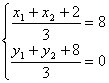
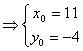
即：BC边中点D的坐标为（11，-4）
2）由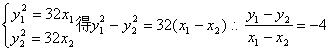
故：BC边所在直线的方程为：4x – y – 40 = 0
20、题解：1）由P为真得：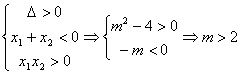
2）由q为真得：
由题意知p、q中有且只有一个为真，一个为假.
.
21、题解：：1) （略）
2) 
是不等式的解，所以有：
，可知a > 1，于是
原不等式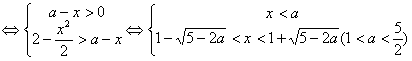
要使不等式的正整数解只有x = 1，则需
22、题解法一：(1)因为点P在椭圆C上，所以
，a=3.
在Rt△PF
故椭圆的半焦距c=
,
从而b2=a2－c2=4,
所以椭圆C的方程为
＝1.
(2)设A，B的坐标分别为（x1,y1）、（x2,y2）. 由圆的方程为（x+2）2+(y－1)2=5,所以圆心M的坐标为（－2，1）. 从而可设直线l的方程为 y=k(x+2)+1,
代入椭圆C的方程得 （4+9k2）x2+(36k2+18k)x+36k2+36k－27=0.
因为A，B关于点M对称. 所以
解得
，
所以直线l的方程为
即8x-9y+25=0. (经检验，符合题意)
解法二：(1)同解法一.
(2)已知圆的方程为（x+2）2+(y－1)2=5,所以圆心M的坐标为（－2，1）.
设A，B的坐标分别为（x1,y1）,(x2,y2).由题意x1
x2且
①
②
由①－②得
③
因为A、B关于点M对称，所以x1+ x2=－4, y1+ y2=2,
代入③得
＝
，即直线l的斜率为，
所以直线l的方程为y－1＝（x+2），即8x－9y+25=0.(经检验，所求直线方程符合题意.)
(3) （略）.