高二年级数学复习试题（1）

高二年级数学复习试题（1）　直线与圆

一.选择题

(1) 平行四边形ABCD的一条对角线固定在A(3,-1),C(2,-3)两点,D点在直线3x-y+1=0上移动，则B点轨迹所在的方程为　　　　　　　　　 (　　　)

A 3x-y-20=0　　　 B 3x-y-10=0　　　　C 3x-y-9=0　　　D 3x-y-12=0

(2)若方程x+y-6+3k=0仅表示一条直线，则实数k的取值范围是　　　  (　 　　)

A (-∞,3)　　　　 B (-∞,0或k=3　　　C k=3　　　　　　 D (- ∞,0)或k=3

(3)入射光线沿直线x-2y+3=0射向直线l: y=x被直线反射后的光线所在的方程是　　(　　　 )

A　x+2y-3=0　　　　 　　　　　　　　　　　　　　 B x+2y+3=0　

C  2x-y-3=0　　 　　　　　　　　　　　　　　　　　D 2x-y+3=0

(4) “a=b”是“直线相切”的　　　　　  (　　　 )

　　　 A 充分不必要条件　　　　　　　　　　　　B 必要不充分条件

　　　 C 充分必要条件　　　　　　　　　　　　　　D 既不充分又不必要条件

(5) 设集合，则A所表示的平面区域(不含边界的阴影部分)是　　 (　 )

　

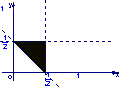
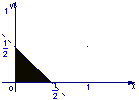
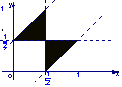
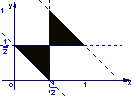
　　　 A 　　　　　　　　　　　　　　B 　　　　　　　　　　　　　　C 　　　　　　　　　　　　　　D　

(6)由动点Ｐ向圆x² + y²=1引两条切线PA、PB,切点分别为A、B，∠APB=60°,则动点Ｐ的轨迹方程为　　　　　　　　　　 (　　　 )

A　x²+y²=4　　　　　　B  x²+y²=3 　　　　　　C　x²+y²=2　　　　　　　　  D　x²+y²=1

(7) 从原点向圆作两条切线，则这两条切线的夹角的大小为（　　 ）

　　　 A 　　　　　　　　　　B 　　　　　　　　　　C 　　　　　　　　　　　 D

(8)已知圆x²+y²+2x-6y+F=0与x+2y-5=0交于A, B两点, O为坐标原点, 若OA⊥OB, 则F

的值为 (　　　 )

A　0　　　　　   B　1　　　　  C　-1　　　　  D　2

(9) 若圆上有且仅有两个点到直线4x+3y=11的距离等于1，则半径R的取值范围是　　　　　　　　　　　　　  　　　　　　　　　　 （　　）

A R>1　　　　B R<3　　　　C 1<R<3　 　　 D R≠2

(10) 已知直线过点，当直线与圆有两个交点时，其斜率k的取值范围是　　　　　　　　　　　　　　　　　　　　　　　  （　　）

A 　　 B C 　 D

二.填空题

(11) 已知圆交于A、B两点，则AB所在的直线方程是__________。

(12)直线上的点到圆的最近距离是　　　　 。

(13)已知圆的方程是x²＋y²＝1，则在y轴上截距为的切线方程为　　　　 。

(14)过P（－2，4）及Q（3，－1）两点，且在X轴上截得的弦长为6的圆方程是______

三.解答题

(15) 半径为5的圆过点A(－2, 6)，且以M(5, 4)为中点的弦长为2，求此圆的方程。

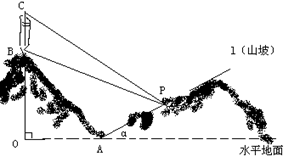
(16) 某人在一山坡P处观看对面山项上的一座铁塔，如图所示，塔高BC=80（米），塔所在的山高OB=220（米），OA=200（米），图中所示的山坡可视为直线l且点P在直线l上，与水平地面的夹角为 , 试问此人距水平地面多高时，观看塔的视角∠BPC最大（不计此人的身高）

(17) 已知定点，点在圆上运动，的平分线交于点，其中为坐标原点，求点的轨迹方程．

(18) 已知圆C：，是否存在斜率为1的直线l，使l被圆C截得的弦AB为直径的圆过原点，若存在求出直线l的方程，若不存在说明理由。

答案

一选择题:

1.A　

[解析]：设点B(x,y),∵平行四边形ABCD的两条对角线互相平分，即AC的中点C（，-2）也是BD的中点，∴点D为（5-x, - 4- y）,而D点在直线

3x-y+1=0上移动，则3(5 – x) – ( - 4 – y)+1=0, 即3x-y-20=0

2.D　

3.C　

[解析]：∵ 入射光线与反射光线关于直线l: y=x对称

　　　　　　　 ∴反射光线的方程为y -2 x +3=0，即2x-y-3=0

4.A　

[解析]： 若a=b，则直线与圆心的距离为等于半径，

∴相切

　　　若相切，则

　　　　　 ∴

故“a=b”是“直线相切”的

 充分不必要条件

5.A　

[解析]：∵x，y，1－x－y是三角形的三边长 ∴x>0,y>0,1-x-y>0,

并且x+y>1-x-y,　x+(1-x-y)>y,　y +(1-x-y)> x

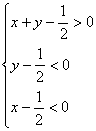∴　　 故选A

6.A　

[解析]：由题设，在直角OPA中， OP为圆半径OA的2倍，即OP=4，∴点Ｐ的轨迹方程为　 x²+y²=4

7.B　　

[解析]：设原点为O，圆心为P，切点为A、B，则OP=6，PA=3，故

则这两条切线的夹角的大小为

8.A　

[解析]：设圆心P到直线的距离为d,则d=0,即AB是直径。

又OA⊥OB，故O在圆上，即F=0

9.C　

[解析]：圆心到直线的距离为2，又圆上有且仅有两个点到直线4x+3y=11的距离等于1，故半径R的取值范围是1<R<3（画图）

10.C

[解析]：直线为，又直线与圆有两个交点

　　　　　　 故　　 ∴

已知直线过点，当时，其斜率k的取值范围

二填空题:  

11. 2x+y=0　  

[解析]：圆相减就得公共弦AB所在的直线方程，

故AB所在的直线方程是

12.

[解析]：　直线上的点到圆的最近距离就是圆心到直线的距离减去半径，即

13.　

[解析]：在y轴上截距为且斜率不存在的直线显然不是切线，

故设切线方程为，则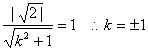

14.(x－1)²＋(y－2)²=13或(x－3)²＋(y－4)²=25　

[解析]：设圆方程为，则

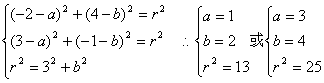
三解答题

(15) 解：设圆心坐标为P(a, b), 则圆的方程是(x－a)²＋(y－b)²=25,

　　　∵ (－2, 6)在圆上，∴ (a＋2)²＋(b－6)²=25, 又以M(5, 4)为中点的弦长为2，　

∴ PM²=r²－², 即(a－5)²＋(b－4)²=20,

　　　联立方程组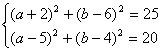, 两式相减得7a－2b=3, 将b=代入　

　　　得　53a²－194a＋141=0, 解得a=1或a=, 相应的求得b₁=2, b₂=,

　　∴ 圆的方程是(x－1)²＋(y－2)²＝25或(x－)²＋(y－)²＝25

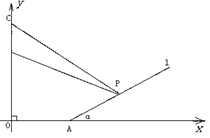
(16) 解：如图所示，建立平面直角坐标系，

则A（200，0），B（0，220），C（0，300），

　　　直线l的方程为即

　　　　设点P的坐标为（x，y），

　　　则

　　  由经过两点的直线的斜率公式

　　　

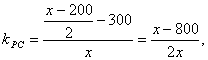
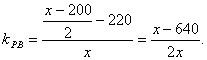
　　　 由直线PC到直线PB的角的公式得

　　　 　　　　　　　 

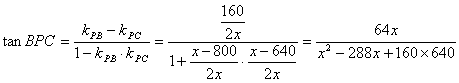
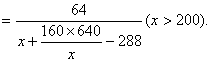
　　　要使tanBPC达到最大，只须达到最小，由均值不等式

　　　

　　　 当且仅当时上式取得等号，故当x=320时tanBPC最大，这时，点P的纵坐标y为

　　　由此实际问题知，所以tanBPC最大时，∠BPC最大，故当此人距水平地面60米高时，观看铁塔的视角∠BPC最大.

(17) 解：在△AOP中，∵OQ是ÐAOP的平分线

　　　　∴

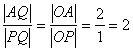
　　设Q点坐标为（x，y）；P点坐标为（x₀，y₀）

　　∴

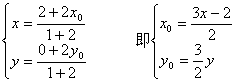
　　∵ P（x₀，y₀）在圆x²+y²=1上运动，∴x₀²+y₀²=1

　　即　　∴　　　　　 

　　此即Q点的轨迹方程。

(18) 圆C化成标准方程为

　　假设存在以AB为直径的圆M，圆心M的坐标为（a，b）

　　由于CM⊥ l，∴k_CM×k_l= -1　 ∴k_CM=，

即a+b+1=0，得b= -a-1　 ①

直线l的方程为y-b=x-a，即x-y+b-a=0　　 CM=

∵以AB为直径的圆M过原点，∴

　　，

　　∴　　②

　　把①代入②得　，∴

当此时直线l的方程为x-y-4=0；

当此时直线l的方程为x-y+1=0

故这样的直线l是存在的，方程为x-y-4=0 或x-y+1=0