高二年级数学期中试卷
一、选择题(每小题5分,共50分)
1. 下列关于算法的说法中,正确的是
A.算法的实质就是解决问题的一般方法,并把解决问题的步骤用具体化、程序化的语言加以表述。
B.对某一确定的问题来说,其算法是唯一的。
C.任何一种算法都必须包含顺序结构、选择结构、循环结构三种结构。
D.算法只有两种表示方法,即用自然语言和流程图表示。
2. 下列变量中具有相关关系的是
A.正方形的面积与边长 B.球的半径与体积
C.匀速行驶车辆的行驶距离与时间 D.人的身高与体重
3.
![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对
4.
设![]() ,那么“
,那么“![]() ”是“
”是“![]() ”的( )条件
”的( )条件
A.充分不必要 B.必要不充分
C.充要 D.既不充分也不必要
5.
已知![]() 的顶点
的顶点![]() 在椭圆
在椭圆![]() 上,顶点
上,顶点![]() 为椭圆的一个焦点,且椭圆的另外一个焦点在
为椭圆的一个焦点,且椭圆的另外一个焦点在![]() 边上,则
边上,则![]() 的周长为
的周长为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6. 函数![]() 的最小值为
的最小值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7. 求方程![]() 的近似正根,要求先将它近似地放在某两个连续整数之间,下面正确的是
的近似正根,要求先将它近似地放在某两个连续整数之间,下面正确的是
A.在![]() 和
和![]() 之间 B.在
之间 B.在![]() 和
和![]() 之间 C.在
之间 C.在![]() 和
和![]() 之间 D.以上都不正确
之间 D.以上都不正确
8. A是圆上固定的一点,在圆周上等可能地任取一点与A连结,弦长超过半径的概率为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9. 设集合![]() ,
,![]() ,椭圆
,椭圆![]() ,其中
,其中![]() ,能构成焦点在
,能构成焦点在![]() 轴上椭圆的概率为
轴上椭圆的概率为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.有限集合![]() 中元素的个数记作
中元素的个数记作![]() ,设
,设![]() 都为有限集合,给出下列命题:
都为有限集合,给出下列命题:
①![]() 的充要条件是:
的充要条件是:![]()
②![]() 的必要条件是:
的必要条件是:![]() ≤
≤![]()
![]() ③
③![]()
![]() 的充分条件是:
的充分条件是:![]() ≤
≤![]()
④![]() 的充要条件是:
的充要条件是:![]() =
= ![]()
其中真命题的个数是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小格4分,共30分)
11.下面是一个算法的伪代码
Read x
![]()
![]() <2
<2 ![]()
![]()
Else
![]()
![]()
![]()
![]()
![]()
![]()
若使输出的y值为-3,则输入的x的值应为___________
![]() 12.茎叶图 0 8 中的中位数是_____________
12.茎叶图 0 8 中的中位数是_____________
1 3 4 6
2 3 6 8
3 3 8 9
4
5 1
 13.命题“
13.命题“![]() ,
,![]() <
<
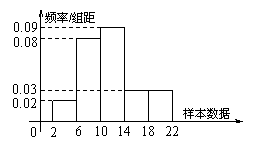
14.右图是容量为![]() 的样本的频率分布直方图,试根据图形中的数据填空。
的样本的频率分布直方图,试根据图形中的数据填空。
⑴样本数据落在范围![]() 内的频率为
内的频率为
⑵总体在![]() 的概率约为
的概率约为
15.已知命题![]() :若实数
:若实数![]() 满足
满足![]() ,则
,则![]() 全为零。命题
全为零。命题![]() :若
:若![]() ,则
,则![]() 给出下列四个复合命题①
给出下列四个复合命题①![]() 且
且![]() ②
②![]() 或
或![]() ③非
③非![]() ④非
④非![]() ,其中真命题是
,其中真命题是
16.已知椭圆![]() ,
,![]() 为椭圆上的一点,
为椭圆上的一点,![]() 为椭圆的左右两个焦点,且满足
为椭圆的左右两个焦点,且满足![]() ,则
,则![]() 的值为
的值为
三、解答题(共80分)
17.命题“已知![]() 是实数,若
是实数,若![]() ,则
,则![]() ”,写出它的逆命题、否命题、逆否命题,并判断这四个命题的真假。(共10分)
”,写出它的逆命题、否命题、逆否命题,并判断这四个命题的真假。(共10分)
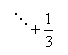 18.用伪代码写出求
18.用伪代码写出求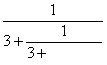 (共有
(共有![]() 个
个![]() )的值的一个算法,并画出流程图。(共12分)
)的值的一个算法,并画出流程图。(共12分)
19.将一颗质地均匀的骰子(它是一种各面上分别标有![]() 的正方体玩具),先后抛掷了
的正方体玩具),先后抛掷了![]() 次,求下列事件的概率:
次,求下列事件的概率:
⑴ 三次点数完全不同;⑵ ![]() 点恰好出现两次;⑶至少出现一次
点恰好出现两次;⑶至少出现一次![]() 点向上。(共12分)
点向上。(共12分)
20.某服装店经营某种服装,在某周内获纯利![]() (元)与该周每天销售这种服装件数
(元)与该周每天销售这种服装件数![]() 之间的一组数据关系见下表:
之间的一组数据关系见下表:
| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
![]() 已知:
已知:![]() ,
,![]() ,
,![]()
⑴求![]() ;⑵画出散点图;⑶求纯利
;⑵画出散点图;⑶求纯利![]() 与每天销售件数
与每天销售件数![]() 之间的线性回归方程。(共14分)
之间的线性回归方程。(共14分)
21.已知关于![]() 的方程
的方程![]() ,
,![]()
求:⑴方程有两个正根的充要条件;
⑵方程至少有一个正根的充要条件。(共16分)
22.已知平面内的一个动点![]() 到直线
到直线![]() 的距离与到定点
的距离与到定点![]() 的距离之比为
的距离之比为![]() ,设动点
,设动点![]() 的轨迹为
的轨迹为![]() ,点
,点![]()
⑴求动点![]() 的轨迹为
的轨迹为![]() 的方程;
的方程;
⑵若![]() 为轨迹为
为轨迹为![]() 上的动点,求线段
上的动点,求线段![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
⑶过原点![]() 的直线交轨迹为
的直线交轨迹为![]() 于
于![]() ,求
,求![]() 面积最大值。(共16分)
面积最大值。(共16分)
参考答案:
一、选择题
ADACC DCBBB
二、填空题
11、![]() 或
或![]() 12、
12、![]() 13、
13、![]() ≥
≥![]()
14、![]() ,
,![]() 15、②④
16、
15、②④
16、![]()
三、解答题
17、原命题为真命题 1分
逆命题:已知![]() 是实数,若
是实数,若![]() ,则
,则![]() 3分
3分
逆命题为假命题 4分
否命题:已知![]() 是实数,若
是实数,若![]() 或
或![]() ,则
,则![]() 6分
6分
否命题为假命题 7分
逆否命题:已知![]() 是实数,若
是实数,若![]() ,则
,则![]() 或
或![]() 9分
9分
 逆否命题为真命题
10分
逆否命题为真命题
10分
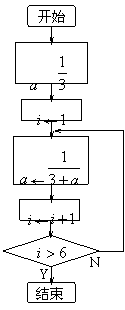
18、(各6分)
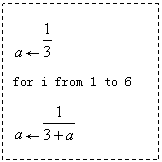 |
19、⑴设“三次点数完全不同”的事件为![]() ,
,
则![]() , 4分
, 4分
⑵ 设“![]() 点恰好出现两次”的事件为
点恰好出现两次”的事件为![]() ,
,
则![]() ,
8分
,
8分
⑶设“至少出现一次![]() 点向上”的事件为
点向上”的事件为![]() ,
,
则![]() 。
12分
。
12分
20、⑴![]()
![]() 4分
4分
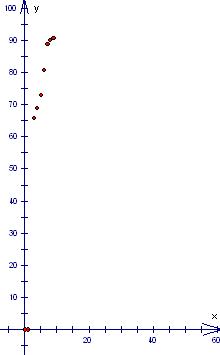 ⑵
8分
⑵
8分
⑶由散点图得,点在一条直线附近摆动,![]() 与
与![]() 具有线性相关关系。 9分
具有线性相关关系。 9分
设线性回归方程为![]() ,
,
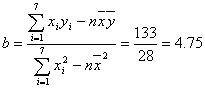 ,
11分
,
11分
![]() 13分
13分
所以纯利![]() 与每天销售件数
与每天销售件数![]() 之间的线性回归方程为
之间的线性回归方程为![]() 14分
14分
21、⑴方程有两个正根![]()
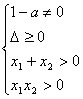 4分
4分
![]()
![]() 或
或![]() 6分
6分
⑵当![]() 时,
时,![]() ,所以
,所以![]() ,有且仅有一个正根。
7分
,有且仅有一个正根。
7分
因为![]() 时方程
时方程![]() 不成立,所以此方程没有零根。8分
不成立,所以此方程没有零根。8分
方程有一个正根和一个负根![]()
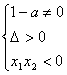 10分
10分
![]()
![]() 12分
12分
方程有两个正根![]()
![]() 或
或![]()
综上所述,方程至少有一个正根的充要条件是![]() 或
或![]() 14分
14分
(“![]() ” 2分)
16分
” 2分)
16分
22、⑴设![]() ,由题意
,由题意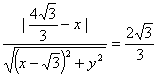
化简得![]() 4分
4分
⑵设![]() ,
,![]() ,由题意得:
,由题意得: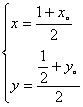
解得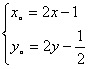 代入
代入![]()
得![]()
即![]() 10分
10分
⑶若![]() 斜率不存在时,
斜率不存在时,![]() 面积为
面积为![]() 。
。
设![]() 斜率为
斜率为![]() ,则
,则![]() 的方程为
的方程为![]() ,
,![]() 到
到![]() 的距离为
的距离为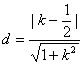
由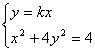 消去
消去![]() 得
得![]()
所以![]()
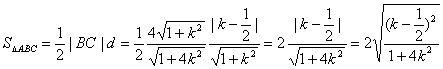
![]() 的最大值为
的最大值为![]() 16分
16分