高二年级笫三次月考数学试卷
时间：120分钟 分值：150分
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
第Ⅰ卷（选择题共60分）
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将其代号选出并填入题后答题卷中的相应位置。
1．若
，则在下列结论中成立的是（ ）
A、
B、
C、
D、
2. 若一椭圆经过点
，且两焦点为
，则它的离心率为（ ）
A、
B、
C、
D、
3．
是方程
表示圆的（ ）条件。
A、必要不充分 B、充分不必要 C、充要 D、既不充分也不必要
4．不等式
的解集是（ ）
A、
B、
C、
D、
5．若方程
表示等轴双曲线，则角
的值为（ ）
A、
或
B、或
C、
或 D或
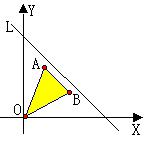
6．如图，已知原点O及点A（1，2），B
，若图中阴影部分（包
括边界）上所有的点都在不等式
所表示的平面区域内，则实
数
的范围是（ ）
A、
B、
C、
D、
7．一个动圆经过定点F（－1，0），且与定直线L：
相切，则此动圆的圆心Ｍ的轨迹方程是（ ）
A、
B、
C、
D、
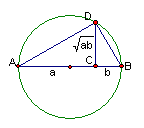
8．设AB是已知圆的直径（如图），C是线段AB上一点，D是
此圆周上一点（不同于A、B），且
，则在下列结论中错误的是（ ）
A、
B、
C、
D、
9．直线
与曲线
的交点个数为（ ）
A、0
B、
10．焦点为（0，6）且与双曲线
有相同渐近线的双曲线方程是
A、
B、
C、
D、
11. 若m、n满足
，则点
的轨迹是
A、整条抛物线 B、抛物线的一部分 C、双曲线的右支 D、椭圆
12. 过双曲线
的右焦点作一直线交双曲线于A、B两点，若AB=10，则这样的直线共有
A、4条 B、3条 C、2条 D、1条
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在答题卷中横线上。
13. 直线
与
轴的夹角的大小为______________。
14. 椭圆{
（
是参数）的一个焦点到相应准线的距离为＿＿＿＿＿。
15. 圆心在直线
上的圆M经过点（2，0），且在
轴上截得的弦长为4，则圆M的标准方程为______________（只要求写出一个即可）。
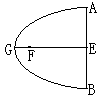
16. 如图，已知某探照灯反光镜的纵切面是抛物线的一部分，
光源安装在焦点Ｆ上，且灯的深度EG等于灯口直径AB，
若灯的深度EG为
G的距离为______cm。
|
| 座位号 | |
高二年级笫三次月考数学试卷答题卷
第Ⅱ卷（非选择题共90分）
| 题号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
一、选择题答题表：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在答题卷中横线上。
13. 14.
15. 16.
三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.
17、（本小题满分12分）在△ABC中，已知顶点A（4，-1），边AB的中点
M（3，2），重心 G（4，2），求顶点B、C的坐标。
|
18、（本小题满分12分）已知圆的半径为
，圆心在直线
上，圆被直线
截得的弦长为
，求圆的方程．
19、（本小题满分12分）求两焦点的坐标分别为（－2，0），（2，0），且经过点
P（2，
）的椭圆方程．
20、（本小题满分12分）已知双曲线经过点M（
），且以直线x= 1为右准线．
（1）如果F（3，0）为此双曲线的右焦点，求双曲线方程；
（2）如果离心率e=2，求双曲线方程．
21、(本小题满分12分）已知双曲线的中心在原点Ｏ，其中一条准线方程为
，且与椭圆
有共同的焦点。
（１）求此双曲线的标准方程；
（２）设直线Ｌ：
与双曲线交于Ａ、Ｂ两点，试问：是否存在实数
，使得以弦AB为直径的圆过点Ｏ？若存在，求出的值，若不存在，请说明理由。
|
22、（本小题满分14分）已知抛物线
的焦点为
，准线与x轴的交点为
，在直线
上找一点M，
（1）使
的值最小，并求这个最小值；
（2）求以
为焦点，经过点M且长轴最短的椭圆方程。
高二年级笫三次月考数学试卷参考答案
一、选择题
1.B 2.A 3. B 4.C 5. C 6. B 7. C 8.D 9.B 10.C 11.B 12.A
二、填空题
13. 
14. 
15. 
或
（写出一个即可）
16. 4
三、解答题
17．解：B（2，5） C（6，2）
18. 解：设圆心坐标为（m，2m）,圆的半径为
，所以圆心到直线x -y=0的距离为 
由半径、弦心距、半径的关系得
所求圆的方程为
19. 解：由题意可知，c=2，设椭圆方程为
，则
①
又点P（2，）在椭圆上，所以
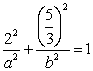②，
联立①②解得，
或
（舍去），
故所求椭圆方程是
20. 解：（1）设P（x，y）为所求曲线上任意一点，由双曲线定义得
= 
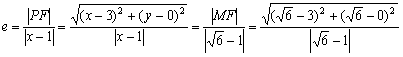化简整理得
（2）
因此，不妨设双曲线方程为
，
因为点M（）在双曲线上，所以
，得
，
故所求双曲线方程为
21. 解：（1）由已知得：
，则
，
因此所求双曲线的标准方程为
。
（2）将代入得
，
则由
得：
，
设
，则
是上述方程的两个根，
由题意知：
，则
，
又
，
，
则
，即
满足条件。
22. 解：由题设条件可知：
（1）设
关于直线的对称点为
，则有
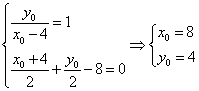，即
。
连接
交直线L于一点，此点即为所求的点M。此时取得最小值，其最小值等于
（2）设所求椭圆方程为：
由（1）可知：椭圆长轴长的最小值为4
即
，又
故所求椭圆方程为：