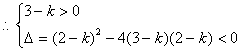高二年数学单元考试卷
姓名--------班级--------座号----------
一、(每小题5分，共60分)选择题
（1）下列说法不正确的是（ ）若
则
A．
B．
C．
D．
（2）下列说法中正确的有（ ）个
A．1个 B．2个 C．3个 D．4个
Ⅰ
Ⅱ
Ⅲ
Ⅳ
(3)直线kx－y＋1＝3k,当k变动时，所有直线都通过定点( )
(A)(0，0) (B)(0，1) (C)(3，1) (D)(2，1)
(4)直线l1:x－y＋
－1＝0绕着它上面一点(1,)沿逆时针方向旋转15°，则旋转后的直线l2的方程为( )
(A)x－y＋1＝0 (B)3x－y＝0 (C)x＋y＋1＝0 (D)3x－y－1＝0
(5)如果AC＜0且BC＜0，那么直线Ax＋By＋C＝0不通过( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(6)直线2x＋3y－6＝0关于直线x＝0对称的直线方程为( )
(A) 2x－3y－6＝0 (B)2x－3y＋6＝0 (C)2x＋3y＋6＝0 (D)2x＋3y－6＝0
（7）给出平面区域如图所示，若使目标函数z=ax+y (a>0)取得最大值的最优解有无穷个，则a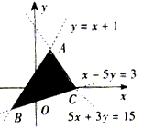
的值为（ ）.
A、 
B、 
C、4 D、 
（8）不等式
的解是
A．
B．
C．
D．以上都不对
(9)直线(
(A)
(B)2 (C)2或 (D)1或
(10) 已知
A．
B．
C．
D．
(11)如果直线经过两直线2x－3y＋1＝0和3x－y－2＝0的交点，且与直线y＝x垂直，则原点到直线l的距离是( )
(A)2
(B)1
(C)
(D)2
(12)已知两点A(1,3),B(－1－5)，在直线2x＋3y＋1＝0上有一点P，使PA＝PB，则P点的坐标是( )
(A)
(B)
(C)(2,－1) (D)(5,0)
二、(每小题6分，共24分)填空题
1. 已知
则
的范围
。
2. 点(1,cosθ)到直线xsinθ＋ycosθ＝1的距离是
(0≤θ≤π)，则θ＝_______
3．已知
，则
与
的大小关系是
。
4． 方程x＋y－1＝2所表示的直线而构成的图形的面积为_____________
三、(12分) 比较
的大小
四、(12分)在△ABC中，BC边上的高所在直线的方程为x－2y＋1＝0,∠A的平分线所在直线的方程为y＝0如果点B的坐标为(1，2)，求边长BC的长。
五、(12分)设同在一条直线上的动点P、Q的坐标分别是(x,y)、(X,Y)，并且坐标间存在关系X＝3x＋2y－1,Y＝3x－2y＋1,当动点P不在平行于坐标轴的直线l上移动时，动点Q在这条直线l垂直且通过点(2,1)的直线上移动，求直线l的方程。
六、(14分)已知直线l:y＝4x和点P(6，4)，在直线
上求一点Q，使过PQ的直线与直线l及x轴在第一象限内围成的三角形的面积最小。
七、（16分）求k的取值范围，对一切实数x，使
恒成立
平面解析几何“直线”检查题 参考答案
一、1）B（2）C（ⅠⅡⅢ）(3)C (4)B (5)C (6)B(7)D（8）D注意函数的定义域(9)A(10) D作差后因式分解(11)C(12)A
二、(1) （1）
，提示：∵
∴
故
∴ (2)
(3) 
提示：作差后因式分解。(4)8
提示：方程x＋y－1＝2所表示的直线为
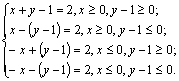
这四条直线围成一个正方形
三、解：由
有当
时
当
四、4
五、3x－y－12＝0或x＋2y－18＝0
提示：设直线的方程为
ax＋by＋c＝0 ①
则动点Q(X,Y)的轨迹为
b(X－2)－a(Y－1)＝0 ②
把X,Y的表示式代入②，得
(3b－
① 与③是同一条直线，所以可得到a、b、c之间的比例关系式。
六、Q(2，8)
提示：设Q(t,4t)，且t＞1，则PQ的方程为
4(t－1)x＋(6－t)y＝20t
PQ交x轴于(
,0)，故所围的三角形的面积为
，
设t－1＝n,则面积
,当n＝
＝1时，有最小值，此时
t＝2,所以Q(2，8)。七解：
即
由已知其解集为R解得
