直线与平面平行的判定和性质同步练习

高二下　9.3 直线与平面平行的判定和性质同步练习

基础练习

　　1．给出下列四个命题：

　　①若一直线与一个平面内的一条直线平行，则这直线与这个平面平行．

　　②若一直线与一平面内的两条直线平行，则这直线与这个平面平行．

　　③若平面外的一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行．

　　④若两条平行直线中的一条与一个平面平行，则另一条也与这个平面平行．

　　其中正确命题的个数是（　）．

　　A．0　　　　　 B．1　　　　　 C．2　　　　　  D．3

　　2．梯形ABCD中，AB∥CD，AB平面a，CD平面a，则直线CD与平面a内的直

　　线的位置关系只能是（　）．

　　A．平行　　　　　　　　　　　　　　　 B．平行或异面

　　C．平行或相交　　　　　　　　　　　　 D．异面或相交

　　3．（1）若直线a、b均平行于平面a，那么a与b的位置关系是__________；

　　（2）若直线a∥b，且a∥平面b，则b与b的位置关系是__________；

　　（3）若直线a、b是异面直线，且a∥b，则b与b的关系是__________．

　　4．如图9－20，在空间四边形ABCD中，E是边AB上的一点，求作过C、E的一个平面，使对角线BD平行于这个平面，并说明理由．

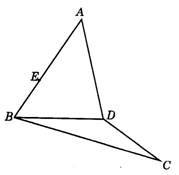
图9－20

　　5．在正方体ABCD－中，E、F分别为和的中点，求证：直线∥平面．

综合练习

　　1．直线与平面平行的充要条件是这条直线与平面内的（　）．

　　A．一条直线不相交

　　B．两条直线不相交

　　C．任意一条直线都不相交

　　D．无数条直线不相交

　　2．给出以下命题，不正确的是（　）．

　　A．如果两条平行线中的一条与一个平面相交，那么另一条也和这个平面相交

　　B．如果直线a和直线b平行，那么直线a平行于经过b的所有的平面

　　C．如果a和b是异面直线，那么经过a有且只有一个平面与直线b平行

　　D．空间四边形相邻两边的中点连线，平行于经过另外两条边的平面

　　3．如图9－21，在空间四边形ABCD中，E、F分别是AB、AD上的点，且AE∶EB＝AF∶FD＝1∶4，又H、G分别是BC、CD的中点，则（　）．

　　A．BD∥平面EFGH，且EFGH是矩形

　　B．HG∥平面ABD，且EFGH是菱形

　　C．HE∥平面ADC，且EFGH是梯形

　　D．EF∥平面BCD，且EFGH是梯形

　　4．设a、b是异面直线，则（　）．

　　A．过不在a、b上的任一点，可作一个平面与a、b都平行

　　B．过不在a、b上的任一点，可作一条直线与a、b都相交

　　C．过不在a、b上的任一点，可作一条直线与a、b都平行

　　D．过a有且只有一个平面与b平行

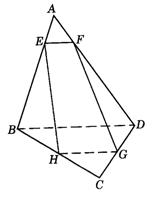
图9－21

　　5．如图9－22，已知a∥a，B、C、D∈a，A与a在平面a的异侧，直线AB、AC、AD分别交a于E、F、G三点，若BC＝5，AD＝7，DG＝4，则EF的长为_________．

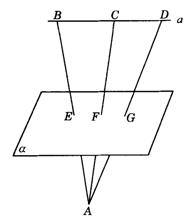
图9－22

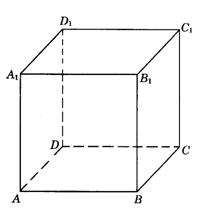
　　6．如图9－23，在正方体ABCD—中，E为上不同于B、的任一点，，．求证：

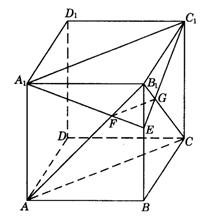
图9－23

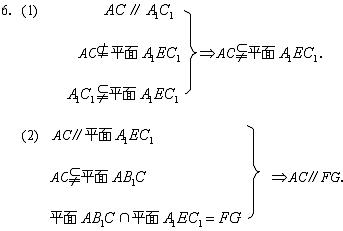
　　（1）AC∥平面；

　　（2）AC∥FG．

　　7．已知三个平面a、b、g 满足＝a，＝b，＝c，且a∥g ，求证：b∥a，c∥b．

　　8．在正方体ABCD—中，E、F分别为BC、的中点，求证：直线EF∥平面．

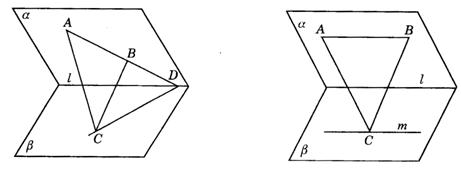
　　9．已知平面a∩平面b＝l，A∈a，B∈a，C∈b （如图9－24），在下列情况下求作平面ABC与平面b的交线，并说明理由．

　　（1）ABl；（2）AB∥l．

　　

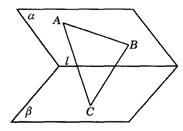
图9－24

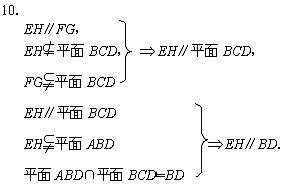
　　10．如图9－25，在空间四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA上的点，且EH∥FG．求证：EH∥BD．

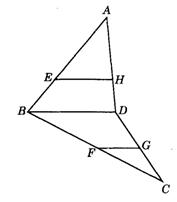
图9－25

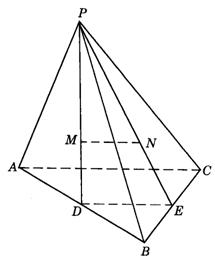
　　11．如图9－26，P为△ABC所在平面外一点，点M、N分别是△PAB和△PBC的重心．求证：MN∥平面ABC．

　　（三角形的三条中线交于一点，称为重心，重心到一个顶点的距离是该点到对边中点距离的2倍）

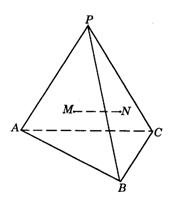
图9－26

参考答案

基础练习

　　1．B．只有③是正确的．

　　2．B．由已知CD∥平面a，a内的直线与CD平行或异面．

　　3．（1）平行、相交或异面．

　　（2）b∥b或bb．

　　（3）b∥b或bb或b与b相交．

　　4．在△ABD内过E点作BD的平行线，交AD于F．连结CE、CF，则BD∥平面CEF．∵BD∥EF（作图），BD平面CEF，EF平面CEF，由直线与平面平行的判定定理可知BD∥平面CEF．

　　5．注意在△中，EF是中位线．

综合练习

　　1．C．

　　2．B．

　　3．D．A选项中“BD∥平面EFGH”正确，但“EFGH是矩形”错误；B选项中“EFGH是菱形”不正确；C选项中“HE∥平面ADC”不正确．

　　4．D．借助正方体这一模型加以排除错误选项．取AB为a，为b，当任一点取时，AB∥平面，但平面．于是A不正确．而与上任一点的连线均在平面内，所以这些直线与AB均无交点，所以B不正确．用反证法说明C不正确，若过任一点有直线与a、b都平行，则由公理4知a∥b，这与a、b异面矛盾．

　　5．∵  E、F、G是平面ABC与平面a的公共点，

　　∴　E、F、G共线，

　　∵　BC∥a，∴　BC∥EF，

　　∴　，∴　

图答9－13

 

　　7．如图答9－14，

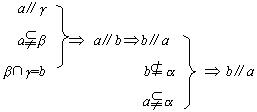
　　同理可证c∥b．

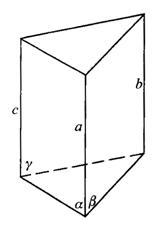
图答9－14

　　8．取BD中点G，连结EG，．可证为平行四边形（还有其他证法）．

　　9．（1）∵ABl，AB与l共面于a，∴  AB与l相交，设AB∩l＝D，连结CD，则CD＝，这是因为D∈AB，D∈l，∴　D∈平面ABC，D∈b，∴　D为平面ABC与平面b 的一个公共点，∴  平面ABC与平面b的交线是过D的一条直线，又C是平面ABC与平面b 的另一个公共点，且平面ABC与平面的交线是过C的一条直线，所以平面＝CD．

图答9－15

　　（2）在平面b内过C作CE∥l，则CE＝．∵　AB∥l，ABb，lb，∴  AB∥平面b．∵  平面ABC与平面b 有一个公共点C，∵　平面ABC与b相交于过C的一条直线m．∵  AB平面ABC， ＝m，AB∥b，∴　AB∥m．∵  AB∥l，∴  l∥m．于是在b 内过C作l的平行线即为所求的交线．

　　

　　11．如图答9－16，连结PM并延长交AB于D，连结PN并延长交BC于E，连结DE．在ΔPAB中，∵  M是ΔPAB的重心，∴  ，同理在△PBC中有，在△PDE中，∵  ，∴　MN∥DE，∵  MN平面ABC，DE平面ABC，∴　MN∥平面ABC．

图答9－16