专题一、二次函数
[基本知识]
1、 二次函数的图象和性质;
2、 二次函数、二次不等式、二次方程的关系。
[例题]
例1、如果函数![]() 在区间
在区间![]() 上有最小值
上有最小值![]() ,那么实数
,那么实数![]() 的值为()
的值为()
A、2 B、![]() C、
C、![]() D、
D、![]()
例2、已知二次函数![]() 的最大值为3,求
的最大值为3,求![]() 的值。
的值。
例3、 二次函数![]() 且
且![]() 时,
时,![]() 当
当![]() 时,
时,![]() 恒成立;
恒成立;
(1)求![]() 之间的关系;
之间的关系;
(2)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得
,使得![]() 在区间
在区间![]() 上是单调函数?若存在,求出
上是单调函数?若存在,求出![]() 的范围,若不存在,说明理由。
的范围,若不存在,说明理由。
例4、设二次函数![]() ,方程
,方程![]() 的两根为
的两根为![]() ,满足
,满足![]() ;
;
(1)当![]() 时,证明:
时,证明:![]()
(2)设函数![]() 的图象关于直线
的图象关于直线![]() 对称,证明:
对称,证明:![]() 。
。
[练习]1、二次函数![]()
(I)用定义证明:当![]() 时,
时,![]() 在
在![]() 上是减函数;
上是减函数;
(II)当![]() 时,在
时,在![]() 上是否存在一个
上是否存在一个![]() 使得
使得![]() ;
;
(III)若![]() 且
且![]() 上,
上,![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
集合
1、
设全集![]() ,集合
,集合![]() ,集合
,集合![]() ,则
,则![]() 的真子集共有
的真子集共有
![]() 个。
个。
2、
已知集合![]() ,则()
,则()
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、
已知全集I=R,集合![]() ,那么()
,那么()
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、已知集合![]() ,若
,若![]() ,则实数
,则实数![]() ( ) A、
( ) A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、
全集为R,![]() (a为常数),且
(a为常数),且![]() 则()
则()
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、
已知集合![]() ,且
,且![]() ,则实数m组成的集合是
,则实数m组成的集合是
7、
![]()
![]() 设全集
设全集![]() ,集合
,集合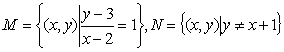 ,那么
,那么![]() 等于
等于
8、
![]() 设集合
设集合![]() ,则集合Q的元素个数为
,则集合Q的元素个数为
9、
![]() 定义
定义![]() ,若
,若![]() ,则
,则![]() =
=
10、某中学高一(1)班有学生50人,参加数学小组的有25人,参加物理小组的有32人,求既参加数学小组,又参加物理小组的人数的最大值与最小值。
专题二:抽象函数
[基本知识]
1、 抽象函数的基本模型。
2、 抽象函数的性质。
3、 抽象函数的求解方法。
[例题]
1、(1)设函数![]() 定义在实数集上,函数
定义在实数集上,函数![]() 与
与![]() 的图象关于()
的图象关于()
A、直线![]() 对称 B、直线
对称 B、直线![]() 对称 C、直线
对称 C、直线![]() 对称D、直线
对称D、直线![]() 对称
对称
![]() (2)设
(2)设![]() 是R上的奇函数,则函数
是R上的奇函数,则函数![]() 是R上的 函数;
是R上的 函数;![]() 是R上的
函数。
是R上的
函数。
![]() (3)如果奇函数在
(3)如果奇函数在![]() 在区间[3,7]上是增函数,那么
在区间[3,7]上是增函数,那么![]() 在区间[-7,-3]上是()
在区间[-7,-3]上是()
A、增函数且最小值为-5 B、增函数且最大值为-5
C、减函数且最小值为-5 D、减函数且最大值为-5
(4)设函数![]() 定义域为R且满足:
定义域为R且满足:
1)![]() ;2)
;2)![]() ;3)
;3)
3)![]() 且
且![]() ;4)
;4)![]()
(5)设![]() 是R上的奇函数,
是R上的奇函数,![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() 等于 ()
等于 ()
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、设函数的定义域为R,并满足条件:存在![]() ,使得
,使得![]() ,又对任何
,又对任何![]()
![]() 成立,证明:
成立,证明:
(1)![]() ; (2)
; (2)![]() 对任何
对任何![]() 都成立。
都成立。
3、已知函数![]() 的定义域为
的定义域为![]() ,且对任意
,且对任意![]() ,恒有
,恒有![]() ;
;
(1)证明:当![]() 时,
时,![]() ;
;
(2)若![]() 时,恒有
时,恒有![]() 成立,则
成立,则![]() 必有反函数;
必有反函数;
(3)设![]() 是的反函数,则
是的反函数,则![]() 在其定义域内恒有
在其定义域内恒有![]() 成立。
成立。
4、设![]() 是定义在R上的偶函数,其图象关于
是定义在R上的偶函数,其图象关于![]() 直线对称,对任意
直线对称,对任意![]() ,都有
,都有![]() ,且
,且![]() ;
;
(I)求![]() ,
,![]() (II)证明
(II)证明![]() 是周期函数;
是周期函数;
(III)记![]() ,求
,求![]() 。
。
练习:1、已知![]() 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且![]() ,若
,若![]() 有
有
![]() ;(I)证明
;(I)证明![]() 是[-1,1]单调函数;(II)解不等式
是[-1,1]单调函数;(II)解不等式![]() 。
。
2、定义在![]() 上的函数
上的函数![]() ,对任意的
,对任意的![]() 都
都![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 成立;
成立;
(1) 设![]() ,求证:
,求证:![]() ; (2)设
; (2)设![]() ,若
,若![]() 比较
比较![]() 的大小;
的大小;
(3)解不等式![]()
专题四:函数![]()
[基本知识]
1、![]() 的性质和图象。
的性质和图象。
2、性质的应用。
[例题]
![]() 例1、(1)设函数
例1、(1)设函数![]() 的图象如图所示,则
的图象如图所示,则![]() 的范围是()
的范围是()
![]() A、
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
![]() (2 )函数
(2 )函数![]() 的值域为
的值域为
例2、
知函数![]() ,
,
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)若对任意![]() 横成立,试求实数
横成立,试求实数![]() 的取值范围。
的取值范围。
例3、已知函数![]()
(1)解不等式![]()
(2)设![]() 时,
时,![]() 的最小值为6,求
的最小值为6,求![]() 的值。
的值。
例4、设计一幅宣传画,要求画面面积为4840![]() ,画面的宽与高的比为
,画面的宽与高的比为![]() ,画面的上、下各留8
,画面的上、下各留8![]() 空白,左右各留5
空白,左右各留5![]() 空白,怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?如果要求
空白,怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?如果要求![]() ,那么
,那么![]() 为何值时,能使宣传画所用纸张面积最小?
为何值时,能使宣传画所用纸张面积最小?
练习:1、设定义域为![]() 的奇函数
的奇函数![]() 是增函数,若当
是增函数,若当![]() 时,
时,
![]()
求![]() 的取值范围。
的取值范围。
2、已知![]() ,函数
,函数![]() ;
;
(1)当![]() 时,若对任意
时,若对任意![]() 都有
都有![]() ,证明:
,证明:![]() ;
;
(2)当![]() 时,证:对任意
时,证:对任意![]() ,
,![]() 的充要条件是
的充要条件是![]() ;
;
(3)当![]() 时,讨论:对任意
时,讨论:对任意![]() ,
,![]() 的充要条件。
的充要条件。
3、已知二次函数:![]() 的图象与
的图象与![]() 轴有两个不同的公共点,若
轴有两个不同的公共点,若![]() ,且
,且![]() 时,
时,![]() ;
;
(1)比较![]() 与
与![]() 的大小; (2)证明:
的大小; (2)证明:![]() ;
;
(3)当![]() 时,求证:
时,求证:![]()
4、二次函数![]() 若
若![]() 的根在
的根在![]() 内,
内,
(1)求证:![]() ; (2)
; (2)![]()
(3)若![]() 有一个根为
有一个根为![]() ,且当
,且当![]() 时,
时,![]() 的最大值为M,求证:
的最大值为M,求证:![]() 。
。
5、已知![]()
(1)若![]() ,
,![]() 在
在![]() 上的最大值为2,最小值为
上的最大值为2,最小值为![]() ,证明:
,证明:![]() 且
且![]() 。
。
(2)若![]() ,
,![]() 是满足
是满足![]() 的实数,且对任意的实数
的实数,且对任意的实数![]() 均满足
均满足![]() ,证明:
,证明:![]() 。
。
高考数学填空题怎么填
填空题是数学高考的三种基本题型之一,其求解方法分为:直接运算推理法、赋值计算法、规律发现法、数形互助法等等. 解题时,要有合理的分析和判断,要求推理、运算的每一步骤都正确无误,还要求将答案表达得准确、完整. 合情推理、优化思路、少算多思将是快速、准确地解答填空题的基本要求. 下面将按知识分类加以例说.
1. 函数与不等式
例1 已知函数![]() ,则
,则![]()
讲解 由![]() ,得
,得![]()
![]() ,应填4.
,应填4.
请思考为什么不必求![]() 呢?
呢?
例2 集合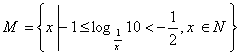 的真子集的个数是
的真子集的个数是![]()
讲解 ![]() ,显然集合M中有90个元素,其真子集的个数是
,显然集合M中有90个元素,其真子集的个数是![]() ,应填
,应填![]() .
.
快速解答此题需要记住小结论;对于含有n个元素的有限集合,其真子集的个数是![]()
例3 若函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]()
讲解 由已知抛物线的对称轴为![]() ,得
,得 ![]() ,而
,而![]() ,有
,有![]() ,故应填6.
,故应填6.
例4 如果函数![]() ,那么
,那么
![]()
讲解 容易发现![]() ,这就是我们找出的有用的规律,于是
,这就是我们找出的有用的规律,于是
原式=![]() ,应填
,应填![]()
本题是2002年全国高考题,十分有趣的是,2003年上海春考题中也有一道类似题:
设![]() ,利用课本中推导等差数列前n项和的公式的方法,可求得
,利用课本中推导等差数列前n项和的公式的方法,可求得
![]()
2. 三角与复数
例5 已知点P![]() 在第三象限,则角
在第三象限,则角![]() 的终边在第
的终边在第![]() 象限.
象限.
讲解 由已知得
![]()
从而角![]() 的终边在第二象限,故应填二.
的终边在第二象限,故应填二.
例6 不等式![]() (
(![]() )的解集为
)的解集为![]() .
.
讲解 注意到![]() ,于是原不等式可变形为
,于是原不等式可变形为
![]()
而![]() ,所以
,所以![]() ,故应填
,故应填![]()
例7 如果函数![]() 的图象关于直线
的图象关于直线![]() 对称,那么
对称,那么![]()
讲解 ![]() ,其中
,其中![]() .
.
![]()
![]() 是已知函数的对称轴,
是已知函数的对称轴,
![]() ,
,
即 ![]() ,
,
于是 ![]() 故应填
故应填 ![]() .
.
在解题的过程中,我们用到如下小结论:
函数![]() 和
和![]() 的图象关于过最值点且垂直于x轴的直线分别成轴对称图形.
的图象关于过最值点且垂直于x轴的直线分别成轴对称图形.
例8 设复数![]() 在复平面上对应向量
在复平面上对应向量![]() ,
,![]() 将
将![]() 按顺时针方向旋转
按顺时针方向旋转![]() 后得到向量
后得到向量![]() ,
,![]() 对应的复数为
对应的复数为![]() ,则
,则![]()
讲解 应用复数乘法的几何意义,得
![]()
![]() ,
,
于是 ![]()
故应填 ![]()
例9 设非零复数![]() 满足
满足 ![]() ,则代数式
,则代数式 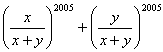 的值是____________.
的值是____________.
讲解 将已知方程变形为 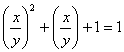 ,
,
解这个一元二次方程,得
![]()
显然有![]() , 而
, 而![]() ,于是
,于是
原式=![]()
=![]()
=![]()
在上述解法中,“两边同除”的手法达到了集中变量的目的,这是减少变元的一个上策,值得重视.
3. 数列、排列组合与二项式定理
例10 已知![]() 是公差不为零的等差数列,如果
是公差不为零的等差数列,如果![]() 是
是![]() 的前n项和,那么
的前n项和,那么
![]()
讲解 特别取![]() ,有
,有![]() ,于是有
,于是有
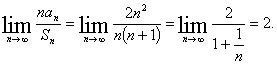 故应填2.
故应填2.
例11
数列![]() 中,
中,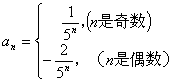
![]() , 则
, 则
![]()
讲解 分类求和,得
![]()
![]()
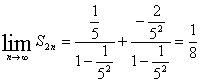 ,故应填
,故应填![]() .
.
例12 有以下四个命题:
①![]()
②![]()
③凸n边形内角和为![]()
④凸n边形对角线的条数是![]()
其中满足“假设![]() 时命题成立,则当n=k+1时命题也成立’’.但不满足“当
时命题成立,则当n=k+1时命题也成立’’.但不满足“当![]() (
(![]() 是题中给定的n的初始值)时命题成立”的命题序号是 .
是题中给定的n的初始值)时命题成立”的命题序号是 .
讲解 ①当n=3时,![]() ,不等式成立;
,不等式成立;
② 当n=1时,![]() ,但假设n=k时等式成立,则
,但假设n=k时等式成立,则
![]() ;
;
③ ![]() ,但假设
,但假设![]() 成立,则
成立,则
![]()
④ ![]() ,假设
,假设![]() 成立,则
成立,则
![]()
故应填②③.
例13 某商场开展促销活动,设计一种对奖券,号码从000000到999999. 若号码的奇位数字是不同的奇数,偶位数字均为偶数时,为中奖号码,则中奖面(即中奖号码占全部号码的百分比)为 .
讲解 中奖号码的排列方法是: 奇位数字上排不同的奇数有![]() 种方法,偶位数字上排偶数的方法有
种方法,偶位数字上排偶数的方法有![]() ,从而中奖号码共有
,从而中奖号码共有![]() 种,于是中奖面为
种,于是中奖面为
![]()
故应填![]()
例14 ![]() 的展开式中
的展开式中![]() 的系数是
的系数是![]()
讲解 由![]() 知,所求系数应为
知,所求系数应为![]() 的x项的系数与
的x项的系数与![]() 项的系数的和,即有
项的系数的和,即有
![]()
故应填1008.
4. 立体几何
例15 过长方体一个顶点的三条棱长为3、4、5, 且它的八个顶点都在同一球面上,这个球的表面积是________.
讲解 长方体的对角线就是外接球的直径![]() , 即有
, 即有
![]()
从而 ![]() ,故应填
,故应填![]()
例16 若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积是 (只需写出一个可能的值).
讲解 本题是一道很好的开放题,解题的开窍点是:每个面的三条棱是怎样构造的,依据“三角形中两边之和大于第三边”,就可否定{1,1,2},从而得出{1,1,1},{1,2,2},{2,2,2}三种形态,再由这三类面构造满足题设条件的四面体,最后计算出这三个四面体的体积分别为:
![]() ,
,![]() ,
,![]() ,故应填.
,故应填.![]() 、
、![]() 、
、![]() 中的一个即可.
中的一个即可.
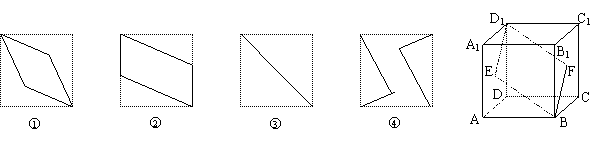 例17 如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
例17 如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
讲解 因为正方体是对称的几何体,所以四边形BFD1E在该正方体的面上的射影可分为:上下、左右、前后三个方向的射影,也就是在面ABCD、面ABB1A1、面ADD1A1上的射影.
四边形BFD1E在面ABCD和面ABB1A1上的射影相同,如图2所示;
四边形BFD1E在该正方体对角面的ABC1D1内,它在面ADD1A1上的射影显然是一条线段,如图3所示. 故应填23.
4. 解析几何
例18
直线![]() 被抛物线
被抛物线![]() 截得线段的中点坐标是___________.
截得线段的中点坐标是___________.
讲解 由![]() 消去y,化简得
消去y,化简得
![]()
设此方程二根为![]() ,所截线段的中点坐标为
,所截线段的中点坐标为![]() ,则
,则
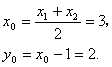
故 应填
![]() .
.
例19 椭圆![]() 上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
讲解 记椭圆的二焦点为![]() ,有
,有
![]()
则知
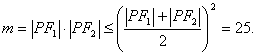
显然当![]() ,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
故应填![]() 或
或![]()
例20 一只酒杯的轴截面是抛物线的一部分,它的函数解析式是![]() ,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
讲解 依抛物线的对称性可知,大圆的圆心在y轴上,并且圆与抛物线切于抛物线的顶点,从而可设大圆的方程为 ![]()
由
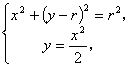
消去x,得 ![]() (*)
(*)
解出 ![]() 或
或![]()
要使(*)式有且只有一个实数根![]() ,只要且只需要
,只要且只需要![]() 即
即![]()
再结合半径![]() ,故应填
,故应填![]()
![]()
填空题的类型一般可分为:完形填空题、多选填空题、条件与结论开放的填空题. 这说明了填空题是数学高考命题改革的试验田,创新型的填空题将会不断出现. 因此,我们在备考时,既要把关注这一新动向,又要做好应试的技能准备.
高考数学选择题怎么选
解答高考数学选择题既要求准确破解,又要快速选择,正如《考试说明》中明确指出的,应“多一点想的,少一点算的”,该算不算,巧判关. 因而,在解答时应该突出一个"选"字,尽量减少书写解题过程,在对照选支的同时,多方考虑间接解法,依据题目的具体特点,灵活、巧妙、快速地选择巧法,以便快速智取. 下面按知识版块加以例说.
1. 函数与不等式
例1
已知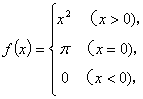 则
则![]() 的值等于( ).
的值等于( ).
A. 0
B. ![]() C.
C. ![]() D. 9
D. 9
讲解 由![]() ,可知选C.
,可知选C.
例2 函数![]() 是单调函数的充要条件是( ).
是单调函数的充要条件是( ).
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
讲解 抛物线![]() 的开口向上,其对称轴为
的开口向上,其对称轴为![]() ,于是有
,于是有![]() 是递增区间,从而
是递增区间,从而![]() 即
即![]() 应选A.
应选A.
例3 不等式![]() 的解集是( ).
的解集是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
讲解 当![]() 与
与![]() 异号时,有
异号时,有![]() , 则必有
, 则必有![]() ,从而
,从而![]() ,解出
,解出![]() ,故应选A.
,故应选A.
例4
关于函数![]() ,有下面四个结论:
,有下面四个结论:
(1)![]() 是奇函数;
是奇函数;
(2)当![]() 时,
时,![]() 恒成立;
恒成立;
(3)![]() 的最大值是
的最大值是![]() ;
;
(4) ![]() 的最小值是
的最小值是![]() .
.
其中正确结论的个数是( ).
A. 1个 B. 2个 C. 3个 D. 4个
讲解 由![]() 是偶函数,可知(1)错;
是偶函数,可知(1)错;
又当![]() 时,
时,![]() ,所以错(2);
,所以错(2);
当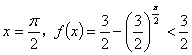 ,故(3)错;
,故(3)错;
从而对照选支应选A.
2. 三角与复数
例5 如果函数y = sin2x + a cos2x的图象关于x=![]() 对称,则a=( ).
对称,则a=( ).
A.![]() B.-
B.-![]() C. 1
D. -1
C. 1
D. -1
讲解 因为点(0,0)与点(![]() ,0)关于直线x=
,0)关于直线x=![]() 对称,所以a必满足:
对称,所以a必满足:
sin0 + a cos0=sin(![]() )+ a cos(
)+ a cos(![]() ),
),
解出a=-1,从而可以排除A, B, C.,故应选D.
例6 在![]() 内,使
内,使![]() 成立的
成立的![]() 的取值范围是( ).
的取值范围是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
讲解 将原不等式转化为![]() 由
由![]() ,知
,知![]() ,从而
,从而![]() ,故应选C.
,故应选C.
事实上,由![]() 显然满足
显然满足![]() ,从而否定A, B, D, 故应选C.
,从而否定A, B, D, 故应选C.
亦可在同一坐标系中,作出函数![]() 和
和![]() 在
在![]() 上的图象,进行直观求解.
上的图象,进行直观求解.
例7 复数![]() 在复平面上对应的点不可能位于( ).
在复平面上对应的点不可能位于( ).
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
讲解 ![]()
由![]() 无解,可知应选A.
无解,可知应选A.
亦可取特值进行排除.事实上
记复数![]() 对应的点为P.若取
对应的点为P.若取![]() ,点P在第二象限;若取
,点P在第二象限;若取![]() ,则点P在第三象限; 若取
,则点P在第三象限; 若取![]() ,则点P在第四象限,故应选A.
,则点P在第四象限,故应选A.
例8 把曲线![]() 先沿
先沿![]() 轴向右平移
轴向右平移![]() 个单位,再沿
个单位,再沿![]() 轴向下平移1个单位,得到的曲线方程是( ).
轴向下平移1个单位,得到的曲线方程是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
讲解 对![]() 作变换
作变换
![]()
得
![]()
即 ![]() .
.
故应选C.
记住一些运动变换的小结论是有效的.本题是函数![]() 向方程式的变式,较为新颖.
向方程式的变式,较为新颖.
3. 数列与排列组合
例9
由![]() 给出的数列
给出的数列![]() 的第34项是( ).
的第34项是( ).
A. ![]() B. 100
C.
B. 100
C. ![]() D.
D. ![]()
讲解 对已知递推式两边取倒数, 得
![]()
即 ![]() .
.
这说明数列![]() 是以
是以![]() 为首项, 3为公差的等差数列, 从而有
为首项, 3为公差的等差数列, 从而有
![]()
即 ![]() 故应选B.
故应选B.
构造等差数列、等比数列是解决数列考题的常用方法, 值得我们重视.
例10 一种细胞,每三分钟分裂一次(一个分裂为两个),把一个这种细胞放入一个容器内,恰好一小时充满;如果开始时把两个这种细胞放入该容器内,那么细胞充满容器的时间为( ).
A. 57分钟 B. 30分钟 C. 27分钟 D.45分钟
讲解 设容器内细胞共分裂n次,则![]() ,即
,即![]() 从而共花去时间为
从而共花去时间为![]() 分钟,故应选A.
分钟,故应选A.
例11 从正方形的6个面中选取3个面,其中有2个面不相邻的选法共有( ).
A. 8种 B. 12种 C. 16种 D. 20种
讲解 采用补集思想求解. 从6个面中任取3个面的取法共有![]() 种方法,其中三个面交于一点共有8种可能,从而满足题意的取法共有
种方法,其中三个面交于一点共有8种可能,从而满足题意的取法共有![]()
![]() 种,故应选B.
种,故应选B.
请读者思考:关系式:![]() 的含义是什么?
的含义是什么?
4. 立体几何
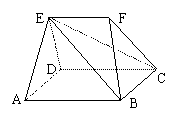 例12 如图,在多面体ABCDEF中,已知面ABCD是边长为3的
例12 如图,在多面体ABCDEF中,已知面ABCD是边长为3的
正方形,EF∥AB,EF与面AC的距离为2,则该多面体的体积为( )
A.![]() B.5
C.6
D.
B.5
C.6
D.![]()
讲解 本题的图形是非常规的多面体,需要对其进行必要的分割.
连EB、EC,得四棱锥E―ABCD和三棱锥E―BCF,这当中,四棱锥E―ABCD的体积易求得![]() , 又因为一个几何体的体积应大于它的部分体积,所以不必计算三棱锥E―BCF的体积,就可排除A, B.,C.,故应选D.
, 又因为一个几何体的体积应大于它的部分体积,所以不必计算三棱锥E―BCF的体积,就可排除A, B.,C.,故应选D.
“体积变换”是解答立体几何题的常用方法,请予以关注.
例13 关于直线![]() 以及平面
以及平面![]() ,下面命题中正确的是( ).
,下面命题中正确的是( ).
A. 若![]() 则
则![]()
B. 若![]() 则
则![]()
![]()
C. 若![]() 且
且![]() 则
则![]()
D. 若![]() 则
则![]()
讲解 对于选支D, 过![]() 作平面P交平面N于直线
作平面P交平面N于直线![]() ,则
,则![]() ,而
,而![]() 从而
从而![]()
又![]() 故
故![]() 应选D.
应选D.
请读者举反例说明命题A, B, C, 均为假命题.
5. 解析几何
例14 过抛物线y=![]() x2(a> 0)的焦点F作一直线交抛物线于P、Q两点,若线段FP与FQ的长分别是p、q,则
x2(a> 0)的焦点F作一直线交抛物线于P、Q两点,若线段FP与FQ的长分别是p、q,则![]() =( ).
=( ).
A. 2a B. ![]() C. 4a D.
C. 4a D. ![]()
讲解 由题意知,对任意的过抛物线焦点F的直线,![]() 的值都是
的值都是![]() 的表示式,因而取抛物线的通径进行求解,则p=q=
的表示式,因而取抛物线的通径进行求解,则p=q=![]() ,所以
,所以![]() =
=![]() ,故应选D.
,故应选D.
例15 点P![]() 到曲线
到曲线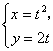 (其中参数
(其中参数![]() )上的点的最短距离是( ).
)上的点的最短距离是( ).
A. 0
B. 1
C. ![]() D. 2
D. 2
讲解 由两点间的距离公式,得点P![]() 到曲线上的点Q
到曲线上的点Q![]() 的距离为
的距离为
![]()
当![]() 时,
时,![]() 故应选B.
故应选B.![]()
将曲线方程转化为![]() ,显然点P
,显然点P![]() 是抛物线的焦点,由定义可知:抛物线上距离焦点最近的点为抛物线的顶点,故应选B.
是抛物线的焦点,由定义可知:抛物线上距离焦点最近的点为抛物线的顶点,故应选B.
例16 已知椭圆![]() =1(a>b>0),双曲线
=1(a>b>0),双曲线![]() =1和抛物线y2=2px(p>0 )的离心率分别为e1、e2、e3,则( ).
=1和抛物线y2=2px(p>0 )的离心率分别为e1、e2、e3,则( ).
A.e1e2>e3 B.e1e2=e3
C.e1e2<e3 D.e1e2≥e3
讲解 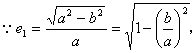
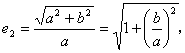
![]()
故应选C.
例17 平行移动抛物线![]() ,使其顶点的横坐标非负,并使其顶点到点
,使其顶点的横坐标非负,并使其顶点到点![]() 的距离比到y轴的距离多
的距离比到y轴的距离多![]() ,这样得到的所有抛物线所经过的区域是
,这样得到的所有抛物线所经过的区域是
A. xOy平面 B. ![]()
C. ![]() D.
D. ![]()
讲解 我们先求出到点![]() 的距离比到y轴的距离多
的距离比到y轴的距离多![]() 的点的轨迹.
的点的轨迹.
设P(x,y)是合条件的点,则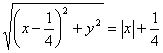 ,
,
两边平方并整理得![]()
![]()
再设平移后抛物线的顶点为![]() ,于是平移后抛物线的方程为
,于是平移后抛物线的方程为
![]()
按a整理得 ![]() .
.
![]() ,化简得
,化简得![]() .故应选B.
.故应选B.
6. 综合性性问题
例18 某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘,根据需要,软件至少买3片,磁盘至少买2盒,则不同的选购方式共有( )
A.5种 B.6种 C.7种 D.8种
讲解 设购买单片软件![]() 片, 磁盘
片, 磁盘![]() 盒, 由题意得
盒, 由题意得
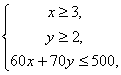
经检验可知,该不等式组的正整数解为:
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
总共有7组, 故应选C.
例19 银行计划将某资金给项目M和N投资一年,其中40%的资金给项目M,60%的资金给项目N,项目M能获得10%的年利润,项目N能获得35%的年利润,年终银行必须回笼资金,同时按一定的回扣率支付给储户. 为了使银行年利润不小于给M、N总投资的10%而不大于总投资的15%,则给储户回扣率最小值为( )
A.5% B.10% C.15% D.20%
讲解 设共有资金为![]() , 储户回扣率
, 储户回扣率![]() , 由题意得解出
, 由题意得解出
![]()
解出 ![]() ,故应选B.
,故应选B.
例20 某电视台的颁奖礼盒用如下方法做成:先将一个奖品放入一个正方体内,再将正方体放在一个球内,使正方体内接于球;然后再将该球放入一个正方体内,球内切于该正方体,再将正方体放入一个球内,正方体内接于球,……如此下去,正方体与球交替出现. 如果正方体与球共有13个,最大正方体的棱长为162cm. 奖品为羽毛球拍、蓝球、乒乓球拍、手表、项链之一,则奖品只能是(构成礼品盒材料的厚度忽略不计)( ).
A . 项链 B. 项链或手表
C. 项链或手表,或乒乓球拍 D. 项链或手表,或乒乓球拍,或蓝球
讲解 因正方体的中心与外接球的中心相同,设正方体的棱长为a,外接球的半径为R,则有
![]() 即
即![]()
![]() 半径为R的球的外切正方体的棱长
半径为R的球的外切正方体的棱长![]() ,
,
![]() 相邻两个正方体的棱长之比为
相邻两个正方体的棱长之比为 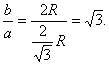
因为有7个正方体,设最小正方体的棱长为t,则
![]() 得
得![]() .
.
故礼品为手表或项链. 故应选B.
高考中的数学选择题一般是容易题或中档题,个别题属于较难题,当中的大多数题的解答可用特殊的方法快速选择. 例如:估值选择法、特值检验法、顺推破解法、数形结合法、特征分析法、逆推验证法、提炼公式法等都是常用的解法. 解题时还应特别注意:数学选择题的四个选择支中有且仅有一个是正确的,因而在求解时对照选支就显得非常重要,它是快速选择、正确作答的基本前提.