高二数学下期期末教学质量评估试卷
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分，考试时间120分钟。第Ⅰ卷1-2页，第Ⅱ卷3-8页。
第Ⅰ卷（选择题，共60分）
一．选择题：本大题共12个小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的，将所选答案填到本试卷后面所附的答题卡中、或按要求涂在答题卡上）
1．甲：A1、A2是互斥事件；乙：A1、A2是对立事件，那么甲是乙的
A．充分但不必要条件 B。必要但不充分条件
C．充要条件 D。既不充分也不必要条件
2．对于任意的直线
与平面
，在平面内必有直线m,使m与
A．平行 B。相交 C。垂直 D。互为异面直线
3．若为一条直线，
，
，
为三个互不重合的平面，给出下列三个命题，其中正确的命题有
①
②
∥
③
∥，
A．0个 B。1个 C。2个 D。3个
4．在棱长为1的正方体
中，
和
分别为
和
的中点，那么直线
与
所成角的余弦值是
A．
B。
C。
D。
5．已知集合
，从这三个集合中各取一个元素构成空间直角坐标系中的点的坐标，则确定的不同点的个数为
A．33 B。
6．在一个口袋中装有5个白球和3个黑球，这些球除颜色外完全相同，从中摸出3个球，则至少摸到2个黑球的概率等于
A．
B。
C。
D。
7．在一个盒子里盛有若干个均匀的红球和白球，从中任取一个球，取到红球的概率为1/3；若从中任取两个球，取到的全是红球的概率为1/11，则盒子里一共有红球和白球
A．6个 B。9个 C。12个 D。24个
8．如图1，在等腰梯形
的中点，将
分别沿
向上折起，使
重合于点
，则三棱锥P－DCE的外接球的体积为
A．
B 
C
D
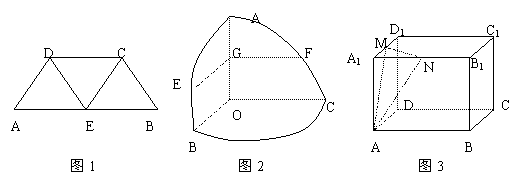
9．口袋里放有大小相等的两个红球和一个白球，有放回地每次摸一个迂，定义数列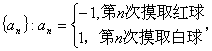
如果
为数列
的前n项和，那么
的概率为
A．
B。
C。
D。
10．如图2，O是半径为1的球心，点A、B、C在球面上，OA、OB、OC两两垂直，E、F分别是大圆弧AB与AC的中点，则点E、F在该球面上的球面距离是
A．
B。
C。
D。
11．如图3，在棱长为有的正方体
的中点，则点
到平面
的距离是
A.-45i B.45i C.-45 D.45
| 座号 |
高二数学下期期末教学质量评估试卷
选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
第Ⅱ卷
二．填空题（本大题共4小题，每小题5分，共20分）
13．从集合
中任取3个元素分别作为直线方程
中的系数A、B、C，所得经过坐标原点的直线共有_________条（用数值表示）
14．已知异面直线a,b所成的角为60°，AB是其公垂线段，E、F分别是异面直线a,b上到A、B距离为2、1的两点，当
=3时，线段AB的长为____________
15. 已知一个简单多面体的各个顶点都有三条棱，那么
16.一个正方体内接于一个球，过球心作一截面，则截面的可能图形是___________（把你认为可能的情况都填上）
 |
三．解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤）
17．（本小题满分10分）某种产品有3只次品和6只正品，每次取出一只测试，直到3只次品全部测出为止，求第三只次品在第6次测试时被测出的不同的测试情况有多少种？（用数值表示）
|
|
|
=
,并由此证明
|
|
|
19．（本小题满分12分）已知
，且二项式
的展开式中第8项和第10项的系数都小于常数，求
的取值范围。
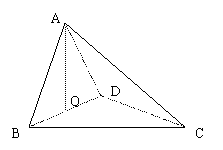20（本小题12分）如图4，四面体ABCD中，O、E分别为BD、BC的中点，且CA=CB=CD=BD=2，AB=AD=
（Ⅰ）求证：
（Ⅱ）求异面直线AB与CD所成角的大小；
（Ⅲ）求点E到平面ACD的距离。
21（本小题满分12分）袋中装有m个红球和n个白球，
,这些红球和白球除了颜色不同以外，其余都相同，从袋中同时取出2个球。
（Ⅰ）若取出的是2个红球的概率等于取出的是一红一白的2个球的概率的整数倍，试证m必为奇数；
（Ⅱ）在m、n的数组中，若取出的球是同色的概率等于不同色的概率，试写出满足
的所有数组（m,n）.
22（本小题满分14分）四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC底面ABCD，
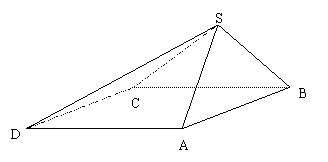已知
（Ⅰ）证明
（Ⅱ）求直线SD与平面SAB所成角的大小。