高二级数学单元测试题《圆锥曲线与方程》
总分100分
一、选择题（每小题5分，共50分）
1. 抛物线
的焦点坐标是（ ）
|
|
|
|
|
|
|
|
|
2. 设双曲线的焦点在
轴上，两条渐近线方程为
，则该双曲线的离心率是（ ）
|
|
|
|
|
|
|
|
|
3. 
是方程
表示椭圆的（ ）
|
| 充分不必要条件 |
| 必要不充分条件 |
|
| 充要条件 |
| 既不充分又不必要条件 |
4. 已知定点
且
，动点
满足
，则
的最小值是（ ）
|
|
|
|
|
|
|
|
|
5. 已知椭圆
，双曲线
和抛物线
的离心率分别为
，则（ ）
|
|
|
|
|
|
|
|
|
6. 若双曲线
的离心率
，则
的取值范围是（ ）
|
|
|
|
|
|
|
|
|
7.
过双曲线
的右焦点
有一条弦
，
,
是左焦点，那么△
的周长为（ ）
|
|
|
|
|
|
|
|
|
8. 设
，常数
，定义运算
为：
，等号右边是通常的乘法运算，如果在平面直角坐标系中，动点的坐标
满足关系式：
，则动点的轨迹方程为（ ）
|
|
|
|
|
|
|
|
|
9.
设
的最小值是（ ）
|
|
|
|
|
|
|
|
|
10. 若椭圆
与双曲线
有公共的焦点
，其交点为，则
△
的面积是（ ）
|
|
|
|
|
|
|
|
|
二、填空题（每小题4分，共20分）
11. 椭圆的焦点是
，为椭圆上一点，且
是
与
的等差中项，则椭圆的方程为____________．
12. 已知点的坐标分别是
，直线
相交于点
，且它们的斜率之积为1，求点的轨迹方程____________．
13. 直线
与抛物线
交于A、B两点，过A、B两点向抛物线的准线作垂线，垂足分别为P、Q ，则梯形APQB的面积为
．
14. 直线
与椭圆
相交于两点，则
____________．
15. 已知直线
与双曲线
的右支相交于不同的两点，则的取值范围是
．
三、解答题（第1题15分；第2题15分）
16. 求标准方程：
（1）若椭圆长轴长与短轴长之比为2，它的一个焦点是
, 求椭圆的标准方程；
（2）若双曲线的渐近线方程为
，它的一个焦点是
，求双曲线的标准方程。
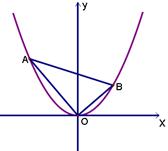
17. 在平面直角坐标系中，抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO（如图所示）.
（Ⅰ）求△AOB的重心G（即三角形三条中线的交点）的轨迹方程；
（Ⅱ）△AOB的面积是否存在最小值？若存在，请求出最小值；若
不存在，请说明理由.
高二级数学单元测试题《圆锥曲线与方程》
班级： 姓名： 座号： 成绩：
一、选择题（每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题（每小题4分，共20分）
11、 12、
13、 14、
15、
三、解答题（第1题15分；第2题15分）
16. 求标准方程：
（1）若椭圆长轴长与短轴长之比为2，它的一个焦点是, 求椭圆的标准方程
（2）若双曲线的渐近线方程为，它的一个焦点是，求双曲线的标准方程
17. 在平面直角坐标系中，抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO
（如图所示）.
（Ⅰ）求△AOB的重心G（即三角形三条中线的交点）的轨迹方程；
（Ⅱ）△AOB的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由.
高二级数学单元测试题《圆锥曲线与方程》答案
一、选择题（每小题5分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | B | C | C | C | Ａ | Ｄ | C | C |
二、填空题（每小题6分，共30分）
11、 
12、 
13、 
14、 
15、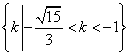 
三、解答题（第1题15分；第2题15分）
1、略解：
（１）椭圆方程：
；（２）双曲线的方程：
2、略解：
解：（I）设△AOB的重心为G(x,y),A(x1,y1),B(x2,y2),则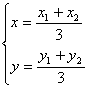
…（1）
∵OA⊥OB ∴
,即
，……(2)
又点A，B在抛物线上，有
，代入（2）化简得
∴
所以重心为G的轨迹方程为
（2）
由（I）得
当且仅当
即
时，等号成立。
所以△AOB的面积存在最小值，最小值是1。