高二级中期考试数学试题
一.选择题（本大题共10小题，每小题5分，共50分），在每小题给出的四个选项中，只有一项是符合题目要求的。
1．设集合p={ x -2< x <3}，Q={ x x +1>2，x∈R}，则集合P∪Q= （ ）
A．{ x -2< x <1} B．{ x 1< x <3}
C．{ x -3< x <3 D．{ x x <-3 或x >-2}
2．若log
A．4 B．
D．9
.
3．设向量
=(1,－3),
=(－2,4),若表示向量4、3－2,
的有向线段首尾相接能构成三角形，则向量为
（ ）
(A)（1，－1） (B)（－1， 1） (C) （－4，6） (D) （4，－6）
4．下列四个命题中的真命题是（ ）
A．经过点
的直线一定可以用方程
表示
B．经过任意两个不同点心
、
的直线都可以用方程
表示
C．不经过原点的直线都可以用方程
表示
D．经过点A（0，b）的直线都可以用方程y=kx+b表示
5．以点（2，－1）为圆心且与直线
相切的圆的方程为
( )
（A）
（B）
（C）
（D）
6.动点P到x轴，y轴的距离之比等于非零常数k，则动点P的轨迹方程是 ( )
A.y=
(x≠0) B.y=kx(x≠0)
C.y=-(x≠0) D.y=±kx(x≠0)
7.（理科做）圆(x-3)2+(y+4)2=2关于直线x+y=0的对称圆的标准方程是 ( )
A.(x+3)2+(y-4)2=2 B.(x-4)2+(y+3)2=2
C.(x+4)2+(y-3)=2 D.(x-3)2+(y-4)2=2
7．（文科做）点A（4，0）关于直线1：5x+4y+21=0的对称点是 （ ）
A．（－6，8） B．（－8，－6） C．（6，8） D．（―6，―8）
8.关于x,y的方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示一个圆的充要条件是 ( )
A.B=0，且A=C≠0 B.B=1且D2+E2-4AF＞0
C.B=0且A=C≠0，D2+E2-4AF≥0 D.B=0且A=C≠0,D2+E2-4AF＞0
9. 椭圆
上一点P到一个焦点的距离为5，则P到另一个焦点的距离为（ ）
A.5
B
10．为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,
A.4,6,1,7 B.7,6,1,
二.填空题（本大体共6小题，每小题4分，共24分）
11．在△ABC中，A（3，-1）、B（-1，1）、C（1，3）写出△ABC区域(包含边界)所表示的二
元一次不等式组 .
12.不等式｜a-b｜≤｜a｜+｜b｜取等号的条件是 .
13.圆x2+y2+ax=0(a≠0)的圆心坐标是 .半径为 .
14.已知直线
过点
，且与
轴、
轴的正半轴分别交于
两点，
为坐标原点，
则三角形
面积的最小值为 .
15. 在数列
中，若
，
，则该数列的通项
。
16．设直线
与圆
相交于
、
两点，且弦
的长为
，则
____________．
三.解答题（本大题共6小题，共76分）解答应写出文字说明，证明过程或演算步骤。
17．（12分）解不等式
．
18．（13分）已知函数
.
(I)求
的最小正周期；
(II)求的的最大值和最小值；
(III)若
，求
的值.
19．（12分）请求出过点A（1，-1）、（-1，1）且圆心在直线x+y-2=0上的圆的方程。
20.（13分）已知直线l:
+ 
=1，M是直线l上的一个动点，过点M作x轴，y轴的垂线，垂足分别为A、B求把有向线段
分成的比λ=2的动点P的轨迹方程.
21（13分）.已知定义域为
的函数
是奇函数。
（Ⅰ）求
的值；
（Ⅱ）若对任意的
，不等式
恒成立，求
的取值范围；
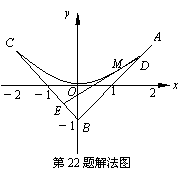22．（13分） 如图,三定点A(2,1),B(0,－1),C(－2,1);
三动点D,E,M满足=t, = t , =t , t∈[0,1]. (Ⅰ)
求动直线DE斜率的变化范围; (Ⅱ)求动点M的轨迹方程.