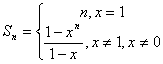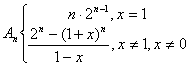高二理科第一学期期中考试数学试卷
说明：本试卷答案均写在答题纸上且解答题答在方框内，否则一律无效。本卷不得使用计算器。
一、选择题（每题5分，共50分）
１、设a,b是两条异面直线，P为a,b外的一点，则下列结论正确的是
(A)过P有一条直线和a,b都平行。 (B) 过P有一条直线和a,b都相交。
(C)过P有一条直线和a,b都垂直 。 (D) 过P有一个平面和a,b都垂直。
2、正四棱锥P-ABCD的所有棱长都相等，E为PC的中点，那么异面直线BE与PA所成的角的余弦值等于
(A)
(B)
(C)
(D)
3、平行六面体中，
(A)
(B) 
(C)4
(D)
4、在
的展开式中，含
的项的系数为
(A)74 (B)121 (C)－74 (D)－121
5、编号为1，2，3，4，5，6的6个不同的小球放入编号为1，2，3，4，5，6的6个不同盒子中，恰好有两个小球的编号与盒子号相同，这样不同的放法有多少种？
(A)120 (B)135 (C)180 (D)240
6、在直三棱柱
，
，则有
(A)
(B) 
(C) 
(D)
7、已知正四棱锥的侧面是正三角形，设相邻两个侧面所成的二面角为
，侧面与底面所成角为
，则
的关系是
(A)
(B) 
(C)
(D) 
8、已知⊙O半径为
，两条直径ＡＢ，ＣＤ交成
角，将圆面沿ＣＤ折成
的二面角，则Ａ，Ｂ两点此时的距离为
(A)
(B) 
(C) 
(D) 
９、化简
(A)
(B)
(C)
(D)
10、将
的方格进行着色，每一方格着一种颜色，相邻方格着不同的颜色，且首尾两格也不同色，现有４种不同的颜色可供选择，则不同的着色方案共有多少种
(A) ２４３种 (B)２４６种 (C)２４０种 (D)２６０种
二填空题（每题4分，共20分）
11、二项式
展开式的常数项为 ▲
.
12、球面上有3个点，其中任意两点的球面距离都等于大圆周长的
，经过这3个点的小圆周长为
，那么这个球面的半径为_______▲___________.
13、在空间四边形OABC中，
点M,N分别为线段OA,BC的中点，则
___▲____.
14、在正方体
中,AB与面
所成角的正弦值为_______▲_________.
15、已知
，化简
▲
.
三．解答题
16、（15分）4名男生和3名女生排成一排，
（1） 3名女生任意两人不能相邻有多少种排法？
（2） 男生甲不站在两端，且男生乙不站在正中间有多少种排法？
（3） 男生甲不站在右端，男生乙不站在左端，男生丙不站在正中间有多少种排法？
17、（10分）棱长为2的正四面体A-BCD内接于一球面，
（1） 求此球面的半径；（2）求此正四面体任意两顶点的球面距离。
18、（12分）设数列
是等比数列，
，公比q是
的展开式的第二项（按x的降幂排列，
）（1）用
表示通项
与前n项和
;(2)若
。
19、（12分）在四棱锥P-ABCD中，
∥CD,AD=CD=2AB,E、F分别为PC、CD的中点；
（1）
试证：
（2）
设
20、(14分)在长方体中,
点E在棱AB上移动，
（1）证明：
（2）当E为AB的中点时，求E到面
的距离；(3)AE等于何值时，二面角
的大小为
。
21、（12分）在四棱柱中所有棱长都等于2，
,平面
,
,(1)求二面角
的大小；（2）求点
到平面
的距离；（3）在直线
上是否有点P，使BP∥面
？若存在求点P的位置；若不存在，说明理由。
22、（5分）把
个不同的小球放入
个盒子中去，每个盒子球数不限，求下列情况下无空盒的放法种数？
（1）个盒子互不相同； （2）个盒子相同。
舟山中学06学年第一学期期中考试高二理科实验班数学答题纸
班级 学号 姓名
一．选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | B | D | B | A | B | A | D | C |
二．填空题
11．
2880 12 13 
14．
15 
三．解答题：
| 16．解：(1)1440 (2)3120 (3)3216 |
| 17．解：(1) |
(2)
| 18．解：（1） |
| 18．（2） |
19.(1)略 （2）
20．(1) 略 (2)
(3)
21.(1) 
(2)
(3)存在。在的延长线上，使＝CP即可。
22．（1）
（2）
。