高二理科数学第一学期期末质量检测试题
一、选择题：本大题共10小题,每小题5分,共50分.在给出的四个选项中，只有一项是符合题目要求的.
1．抛物线
＝－2y2的准线方程是
A．
B．
C．
D．
2．若a＞b＞c, 则下列不等式中一定成立的是
A．ab＞ac B．a (b2＋c2)＞c(b2＋c2) C． ab ＞ bc D．a c ＞b c
3．两圆x2＋y2＝4与
的位置关系是
A．相交 B．相切 C．相离 D．不确定
4．设P是双曲线
上一点，双曲线的一条渐近线方程为3x－2y=0，F1、F2分别是双曲线的左、右焦点．若
，则
＝
A. 1或5 B.
5．若
，
，则下列不等式一定成立的是
A.
, 
B. 
，
C.
，
D. 
，
6．直线xcosθ+y-1=0(θ∈R)的倾斜角的范围是
A. [0,π)
B. 
∪
C. 
D.
7．设0＜a＜
，则下列不等式中一定成立的是
A．
B．
C．
D．
8. 抛物线y2=2px与直线ax+y－4=0交于两点A、B，其中点A的坐标是(1, 2)，设抛物线的焦点为F，则
等于
A.
5 B.
6． C.
D.
7
9．在R上定义运算
．若方程 
有解，则k的取值范围是
A．
B﹒
C﹒
D﹒
10．已知椭圆
( a > b > 0) 的离心率为
，准线为
、
；双曲线
离心率为
，准线为
、
；若、、、正好围成一个正方形，则
等于
A. 
B
.
C.
D. 
二、填空题：本大题共5个小题,每小题4分,共20分.把答案直接填在题中横线上.
11. 不等式
≤0的解集是 .
12. 若直线x＋3y－7＝0与直线kx－y－2＝0的方向向量分别为
，则当
时，实数k的值为
.
13. 若直线
始终平分圆
的圆周，则
的最小值为
.
14. 椭圆的中心在直角坐标系的原点，左焦点为(－
, 0)，且右顶点为D（2，0），设点A的坐标是
，点P是椭圆上的动点，则线段PA中点M的轨迹方程是 .
15. 给出下列四个命题：① 两平行直线
和
间的距离是
；② 方程
可能表示椭圆；③ 若双曲线
的离心率为e，且
，则k的取值范围是
；④ 曲线
关于原点对称．其中所有正确命题的序号是_____________ .
三、解答题: 本大题共6个小题，共80分.解答应写出必要的文字说明,证明过程或演算步骤.
16. (本小题满分12分)
求以点(－2, 3)为圆心，且被直线x+y=0截得的弦长为
的圆方程.
17. (本小题满分13分)
已知不等式
.
⑴. 求a，b的值，
⑵. 若c>1，解不等式
.
18. (本小题满分13分)
怀化啤酒厂生产淡色和深色两种啤酒.粮食、啤酒花和麦芽是三种有约束的资源，每天分别可以提供480斤、160两和1320斤.假设生产一桶淡色啤酒需要粮食5斤、啤酒花4两、麦芽20斤；生产一桶深色啤酒需要粮食15斤、啤酒花4两、麦芽40斤；售出后，每桶淡色啤酒可获利15元，每桶深色啤酒可获利25元.假设每天生产出的啤酒都可售完，问每天生产淡色和深色两种啤酒各多少桶时，工厂的利润最大？
19. (本小题满分14分)
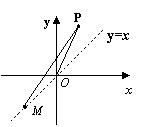
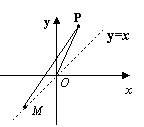
如图，点P(a, b)在第一象限内，且在直线y=x的左侧，点M(－m, －m)在第三象限内， O为原点 .
(1). 由图可知，直线PM与直线PO的斜率哪个较大？
(2). 试用不等式的语言描述上述事实：“若 ，
则 < ”；
(3). 用代数方法证明你的结论.
20. (本小题满分14分)
已知椭圆C1的方程为
，双曲线C2的左、右焦点分别为C1的左、右顶点，而C2的左、右顶点分别是C1的左、右焦点.
(1). 求双曲线C2的方程；
(2). 若直线l：
与椭圆C1及双曲线C2恒有两个不同的交点，且l与C2的两个交点A和B满足
(其中O为原点)，求k的取值范围.
21. (本小题满分14分)
有对称中心的曲线叫做有心曲线. 显然圆、椭圆、双曲线都是有心圆锥曲线. 我们称下列定义为椭圆的第三定义：
定义：直角坐标平面内的一个动点M(x,y)到两定点A1 (－a, 0), A2 (a, 0)(a≠0)的斜率乘积等于常数λ(λ<0, 且λ≠－1)的点的轨迹（连同定点A1、A2 ）叫做椭圆.
⑴. 请用类似的方法写出双曲线的第三定义，并加以证明；
⑵. 请用类似的方法写出圆的定义（不必证明）， 你能从上述定义中得到有心圆锥曲线(包括椭圆、双曲线、圆)的统一定义吗？请写出你的结论（不必证明）.
高二理科数学试题参考答案及评分意见
一、选择题：每小题5分,共50分.
1-5. DBCCA；6-10. BADBA；
二、填空题：每小题4分,共20分.
11. {x│1＜x≤2}； 12. 3； 13. 4； 14.
；15. ①，②，④.
三、解答题：共6小题, 共80分.
16. 解：由已知，圆心(－2, 3)到直线x+y=0的距离：
…………3分
设圆的半径为r, 则有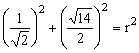 
，
………………………7分
∴ r2=4， ……………………………10分
故所求圆的方程为 (x+2)2+(y－3)2=4 ……………………………12分
17. 解：（1）原不等式可化为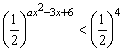 
等价于 ax2－3x+6>4, 即 ax2－3x+2>0, ………………3分
由题设 x=1是方程ax2－3x+2=0 的解，∴ a×12－3×1+2=0, 得 a=1. ………4分
原不等式等价于 x2－3x+2>0
x<1, 或x>2, ∴ b=2. ………………6分
（2）由a=1，b=2，得原不等式为
，
………………7分
∵ c>1 ∴ 1<c<2时，不等式的解集为{x1<x<c, 或x>2}； ………………9分
c=2时，不等式的解集为{x1<x<2, 或x>2}； ………………11分
c>2时，不等式的解集为{x1<x<2, 或x>c}. ………………13分
18. 解：设每天生产淡色和深色两种啤酒分别为x、y桶,每天的利润为
元，
则z=15x+25y=5(3x+5y), (x, y∈N) ……………2分
依题意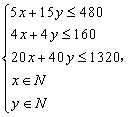得： 
化简得：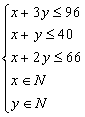
……………5分
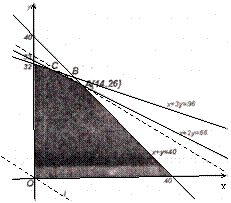
作出可行域如图： ……………8分
作直线l0：3x+5y=0把l0向右上方平行移动到过点A的位置时，直线在y轴上的截距最大，此时目标函数z=15x+25y取得最大值.
……………10分
又由
得A (14, 26),
∴当x=14，y=26时，zmax=860元 . ……………………………12分
答：每天生产淡色和深色两种啤酒分别为14和26桶时,每天的利润最大. …………13分
19. 解：(1). kPM<kPO ； ………………………3分
(2). 若0<a<b，m>0，则
………………………7分
证明： (3). ∵ 
…………………10分
又 0<a<b，m>0，∴ m(a－b)<0, a(a+m)>0
∴ 
, ………………………12分
∴ 
成立
………………………14分
注：其他证明方法酌情记分.
20. 解：（1）设双曲线C2的方程为
，则
故C2的方程为
………………………………………………5分
（2）将
由直线l与椭圆C1恒有两个不同的交点得
即 
①…………7分
.
由直线l与双曲线C2恒有两个不同的交点A，B得
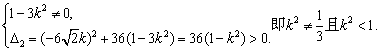② …………9分
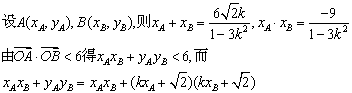
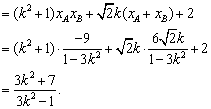
解此不等式得
③…………12分
由①、②、③得
故k的取值范围为
………………14分
21. 解：⑴.双曲线的第三定义：直角坐标平面内的一个动点M(x,y)到两定点A1 (－a, 0), A2 (a, 0) (a≠0)的斜率乘积等于常数λ(λ＞0)的点的轨迹（连同定点A1、A2 ）叫做双曲线.
…………………………3分
证明如下：
∵ 
，
(x≠±a)
∴ 
，
…………………………5分
即： y2=λx2－λa2
λx2－y2=λa2
， (x≠±a)
……………………7分
∵ λ＞0，a≠0，
∴ 方程所表示的曲线（连同定点A1、A2 ）是双曲线. ……………9分
⑵. 圆的定义：直角坐标平面内的一个动点M(x,y)到两定点A1 (－a, 0), A2 (a, 0)(a≠0)的斜率乘积等于－1的点的轨迹（连同定点A1、A2 ）是圆. ……………………11分
有心圆锥曲线的统一定义：直角坐标平面内的一个动点M(x,y)到两定点A1 (－a, 0),
A2 (a, 0)(a≠0)的斜率乘积等于常数λ（λ≠0）的点的轨迹（连同定点A1、A2 ），
当λ<0, 且λ≠－1时是椭圆；当λ=－1时是圆；当λ＞0时, 是双曲线.
……………………14分