高二年级第二学期期中考试数学试卷
考试时间:120分钟 满分:150分
(请在答题卷上答题)
一、 选择题:本大题共12小题;每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求.
1.在空间四边形ABCD各边上分别取E、F、G、H四点,如果EF与GH能相交于点P,那么 ( )
A.点P必在直线AC上 B.点P必在直线BD上
C.点P必在平面ABC内 D.点P必在平面ABC外
2、已知两条直线a、b及平面α有四个命题:
①若a∥b且a∥α则b∥α; ②若a⊥α且b⊥α则a∥b;
③若a⊥α且a⊥b则b∥α; ④若a∥α且a⊥b则b⊥α; 其中正确的命题是( )
A ① B② C ③ D ④
3. 设M、O、A、B、C是空间的点,则使M、A、B、C一定共面的等式是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
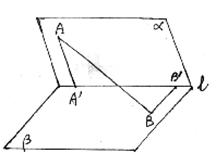
4. 二面角α—EF—β是直二面角C∈EF,AC![]() α,BC
α,BC![]() β,∠ACF=30°,∠ACB=60°,
β,∠ACF=30°,∠ACB=60°,
则cos∠BCF等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5. 已知点A(1,0,0),B(0,1,0),C(0,0,1),若存在点D,使得DB∥AC,DC∥AB,则D点的坐标是 ( )
A.(-1,1,1)
B.![]()
 C.(-1,1,1)或(1,-1,-1) D.
C.(-1,1,1)或(1,-1,-1) D.![]()
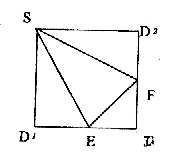
6. 如图,E, F分别是正方形SD1DD2的边D1D,DD2的中点,
沿SE,SF,EF将其折成一个几何体,使D1,D,D2重合,记作
D.给出下列位置关系:①SD⊥面DEF; ②SE⊥面DEF;
③DF⊥SE; ④EF⊥面SED,其中成立的有: ( )
A. ①与② B. ①与③
C. ②与③ D. ③与④
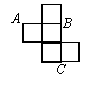 7. 如图,是一个无盖正方体盒子的表面展开图,
7. 如图,是一个无盖正方体盒子的表面展开图,![]() 为其上的三个
为其上的三个
点,则在正方体盒子中,![]() 等于 …………………… ( )
等于 …………………… ( )
(A) 45° (B) 60° (C) 90° (D) 120°
(请在答题卷上答题)
8、在30°的二面角a-l-b中,P∈a,PQ⊥b,垂足为Q,PQ=
 (A)
(A)![]() a (B)
a (B)![]() a (C)a (D)
a (C)a (D)![]() a
a
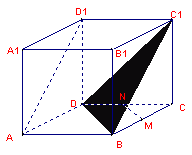
9、右图的正方体中,M、N是棱BC、CD的中点,
则异面直线AD1与MN所成的角为 ( )度
A. 30 B
10、 下图所示的直观图,其平面图形的面积是( )
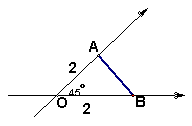
A.4 B. ![]() C. 2
C. 2![]() D. 8
D. 8
11.已知长方体![]() 中,
中,![]() ,若棱
,若棱![]() 上存在点
上存在点![]() ,使得
,使得
![]() ,则棱
,则棱![]() 的长的取值范围是 ………………………………… ( )
的长的取值范围是 ………………………………… ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D) ![]()
12、长方体ABCD—A1B1C1D1中,AB=2,BC=3,AA1=5,则一只小虫从A点沿长方体的表面爬到C1点的最短距离是 ( )
A ![]() B 5
B 5![]() C 17
C 17![]() D 3+
D 3+![]()
二、填空题(本题每小题5分,共20分)
13.已知两异面直线![]() 所成角为
所成角为![]() ,直线
,直线![]() 分别与
分别与![]() 所成的角都是q ,则q 的
所成的角都是q ,则q 的
取值范围是 .
14.已知正方形![]() ,
,![]() 相交于点
相交于点![]() .若将正方形
.若将正方形![]() 沿对角线
沿对角线![]() 折
折
成60°的二面角,并给出下列四个结论:
①![]() ;②
;②![]() ;③
;③![]() 为正三角形;④
为正三角形;④![]() .
.
则其中正确命题的序号是: .(注:把你认为正确命题的序号都填上)
15.在等腰△ABC中,AC=12,∠BAC=120°,△ABC所在平面外一点P到A、B、C的距离都是![]() ,则P到平面ABC的距离为
.
,则P到平面ABC的距离为
.
16. 在△ABC中,∠ABC=90°,AB=BC=a,BD⊥AC于D,以BD为棱折成直二面角A—BD—C,P是AB上的一点,若二面角P—CD—B为60°,则AP= .
高二第二学期期中考试数学答题卷
班级 姓名 得分
答题卷
一、 选择题:(每题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(本大题共4题,每小题5分,共20分)
13. 14. 15. 16.
三. 解答题(本大题共5题,总分70分)
17.如图,二面角![]() ,
,![]() 。
。
|
(1)求![]() ;
;
(2)求AB与l所成的角.(12分)
|
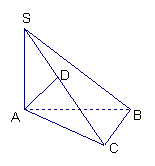 18、已知△ABC,∠ACB=90,SA⊥面ABC,AD⊥SC
18、已知△ABC,∠ACB=90,SA⊥面ABC,AD⊥SC
求证:AD⊥面SBC(10分)
19.A是△BCD所在平面外的点,∠BAC=∠CAD=∠DAB=60°,AB=3,AC=AD=2.
(Ⅰ)求证:AB⊥CD;
(Ⅱ)求AB与平面BCD所成角的余弦值. (16分)
|
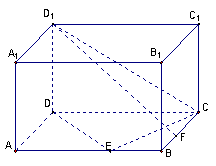 20.如右图,在长方体ABCD—A1B1C1D1中,已 知AB= 4, AD =3,AA1= 2. E、F分别是线段AB、BC上的点,且EB= FB=1.
20.如右图,在长方体ABCD—A1B1C1D1中,已 知AB= 4, AD =3,AA1= 2. E、F分别是线段AB、BC上的点,且EB= FB=1.
(1)求直线EC1与FD1所成的余弦值;
(2)求二面角C—DE—C1的正切值.(16分)
21、已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,
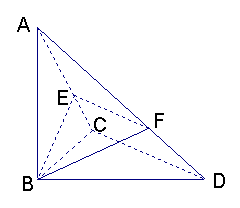 ∠ADB=60°,E、F分别是AC、AD上的动点,且
∠ADB=60°,E、F分别是AC、AD上的动点,且![]() <λ<1)
<λ<1)
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD? (16分)
|
高二数学参考答案
1.A
2.B;3.D;4.D;5.A;6.B;7.B;8.A;9.C;10.A;11.C;12.B..14.
①④;15.5;16. ![]()
17.


18、证明:![]()
![]()
又![]() 面
面![]()
![]()
![]() 面
面![]()
![]()
又![]()
![]()
![]() 面
面![]()
19.(Ⅰ)∵∠BAC=∠CAD=∠DAB=60°, AC=AD=2,AB=3, ∴△ABC≌△ABD,BC=BD.
取CD的中点M,连AM、BM,则CD⊥AM,CD⊥BM. ∴CD⊥平面ABM,于是AB⊥BD.
(Ⅱ)由CD⊥平面ABM,则平面ABM⊥平面BCD,这样∠ABM是AB与平面BCD所成的角.
在△ABC中,AB=3,AC=2,∠BAC=60°,![]() .
.
在△ACD中,AC=AD=2,∠CAD=60°,
∴△ACD是正三角形,AM=![]() . 在Rt△BCM中,BC=
. 在Rt△BCM中,BC=![]() ,CM=1,
,CM=1,
![]() .
.![]()
20.解:(1)以A为原点,![]() ,
,![]() ,
,![]() 分别为x轴,y轴,z轴的正向建立空间直角坐标系, 则有D(0,3,0)、D1(0,3,2)、E(3,0,0)、
分别为x轴,y轴,z轴的正向建立空间直角坐标系, 则有D(0,3,0)、D1(0,3,2)、E(3,0,0)、
|
![]() =(3,-3,0),
=(3,-3,0),![]() =(1,3,2),
=(1,3,2), ![]() =(-4,2,2)
=(-4,2,2)
设EC1与FD1所成角为β,则
cosβ=![]() =
=![]() =
=![]()
(2)设向量![]() =(x,y,z)与平面C1DE垂直,则有
=(x,y,z)与平面C1DE垂直,则有
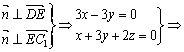 x=y=-
x=y=-![]() z
z
∴![]() =(-
=(-![]() ,-
,-![]() ,z)=
,z)=![]() (-1,-1,2)其中z>0
(-1,-1,2)其中z>0
取![]() =(-1,-1,2),则
=(-1,-1,2),则![]() 是一个与平面C1DE垂直的向量,
是一个与平面C1DE垂直的向量,
∵向量![]() =(0,0,2)与平面CDE垂直,
=(0,0,2)与平面CDE垂直,
∴![]() 与
与![]() 所成的角θ为二面角C-DE-C1DE的平面角.
所成的角θ为二面角C-DE-C1DE的平面角.
∵cosθ=![]() =
=![]()
![]() ∴tanθ=
∴tanθ=![]()
21、证明:(Ⅰ)∵AB⊥平面BCD, ∴AB⊥CD,
∵CD⊥BC且AB∩BC=B, ∴CD⊥平面ABC.
又![]()
∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF![]() 平面BEF,
平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC.
(Ⅱ)由(Ⅰ)知,BE⊥EF,又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC.
∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴![]()
![]() 由AB2=AE·AC 得
由AB2=AE·AC 得![]()
|