高二年级第三次月考数学试题

高二年级第三次月考数学试题

一.选择(5分×10=50分):

1.在原命题及其逆命题、否命题、逆否命题中，真命题的个数可以是（　　）

A．1或2或3或4　 　B．0或2或4 　 C．1或3　　　D．0或4

2.有4个命题：（1）没有男生爱踢足球；（2）所有男生都不爱踢足球；

（3）至少有一个男生不爱踢足球；（4）所有女生都爱踢足球；

其中是命题“所有男生都爱踢足球”的否定是　　　　　 （　 　）

　 A．（1）　　　　 B．（2）　　 　 C．（3）　　　 D．（4）

3.如果x、y是实数，那么xy>0是x+y=x+y的　　　 条件（　　）

A．充分不必要  　B．必要不充分　 C．充要条件　D．既不充分又不必要

4.命题则在下述判断：①p或q为真；②p或q为假；③p且q为真；④p且q为假；⑤非p为真；⑥非q为假．

其中正确的的个数为　　　　　　　　　　 （　　）

 A.2　 　　　　　B．3　　　　　 C.4　　　　　 D.5　　　 　　　　 

5.如果椭圆上一点P到焦点F₁的距离为6，则点P到另一个焦点F₂的距离为（　 ）

A． 10　　　　　B． 6  　　　 C． 12　　 　　D． 14

6. 在同一坐标系中，方程a²x²+b²y²=1与ax+by²=0（a＞b＞0）的曲线大致是（　　）

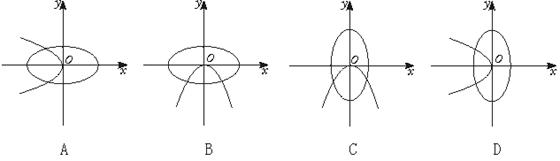
7.动圆C经过定点F(0, 2),且与直线y+2=0相切,则动圆的圆心C的轨迹方程是(　　)

A.x²=8y　 　 B.y²=8x　　　　C.y=2　　 D.x=2

8. 曲线y=x³+4x-2在点P₀处的切线平行于直线y=4x-1,则P₀的坐标是(　 )

A.(0,-2)　　　　 B.(1,0)　　　　  C.(-1,0)　　　 　D.(1,4)

9.函数f(x)=x³ +ax² +bx +c,其中a,b,c为实数,当a²-3b<0时,f(x)在

R上是　　　　　　　　　　　 (　　　)

　 A．增函数　　  B.减函数　 C.常数　  D.不是单调函数,也不是常数

10.若双曲线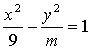的渐近线方程为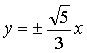，则双曲线焦点F到渐近线的距离为 (　)　　　　

 A．2　　　　　 B．　　　　 C．　　　　 D．2

题号	1	2	3	4	5	6	7	8	9	10
答案

二.填充(5分×6=30分):

11.设A是C的充分条件，B是C的充分条件，D是C的必要条件，D是B的充分条件，那么A是B的__________　　 条件．

12.抛物线y=4ax²(a≠0)的焦点坐标是 　　　　　　　  .　

13.物体的运动方程是S=－t³＋2t²－5,则物体在t=3时的瞬时速度为　　　　　  .

14.过,且两条渐进线为y=±3x的双曲线的方程为　　　　　　　　 .

15.设△ABC的三边分别为a,b,c，命题“若a²+b²≠c²，则△ABC不是直角三角形”的逆否命题是　　　　　　　　　　　 　　　　　　　　　  .

16.若方程表示双曲线,则实数k的取值范围是　　　　　　　   .

三.解答(80分):

17.设p: 函数y=c^x是R上的单调减函数；q：1-2c<0,若p或q是真命题，

p且q是假命题，求c的取值范围.　　(13分)

18.已知直线y=x+1与椭圆交于A,B两点,

(1)求线段AB中点M的坐标;

(2)求线段AB的长.　　　 (13分)

19.用导数的定义证明.　 (13分)

20.已知函数

(1)求函数f(x)的导数;　　  (2)求函数f(x)的极值.　 　(13分)

21.已知定点A（1，0），定直线 :x=5，动点M（x,y）

 (1)若M到点A的距离与M到直线的距离之比为,试求M的轨迹曲线C₁的方程；

(2)若双曲线C₂是以C₁的焦点为顶点，且以C₁的顶点为焦点，试求双曲线C₂的方程；　  (14分)

22.已知函数的图象过点P（0，2），且在点

M（－1，f（－1））处的切线方程为.

（1）求函数的解析式；（2）讨论函数的单调性. (14分)

答案：

一.选择：　　BCACD　DAAAC

二.填充：

(11)充分　　 (12)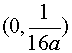　　 (13)3　　 (14)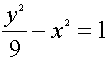

(15)若△ABC是直角三角形,则a²+b²=c²  (16)k<1或k>3

三.解答:

(17)

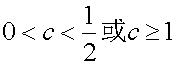
(18)①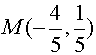　　　　②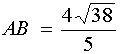

(19)略

(20)①f′(x)=-x²+4　　　

②f(x)_极小值=f(-2)=-5 ; f(x)_极大值=f(2)=

(21) ①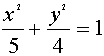　 ②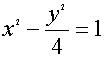

(22) ①f(x)=x³-3x²-3x+2

②f(x)在上为单调增函数;

在上为单调减函数.