高二年级数学第一学期期中考试
试题
命题单位：荡口中学 命题人：王丽芸 审核人：王峰
一、选择题：（共12题，每小题5分）
1、抛掷一枚质地均匀的硬币，如果连续抛掷1000次，那么第999次出现正面朝上的概率是 （ ）
（A） 
（B） 
（C） 
（D） 
2、要从已编号（1～50）的50部新生产的赛车中随机抽取5部进行检验，用系统抽样方法确定所选取的5部赛车的编号可能是 （ ）
（A）15，10，15，20，25 （B） 3，13，23，33，43
（C） 5， 8，11，14，17 （D） 4，8，12，16，20
3、下图给出的是计算
…+
的值的一个程序框图，其中判断框内应填入的条件是
（ ）
（A）I>100 （B）I≤100 （C）I>50 （D）I≤50
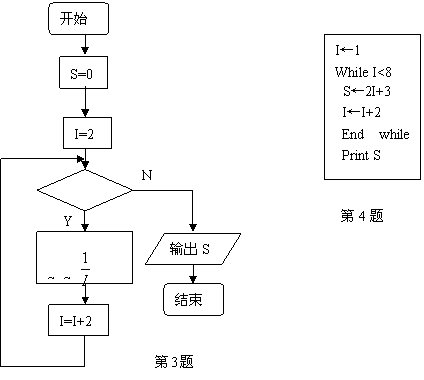
4、根据如图所示的伪代码，可知输出结果为 （ ）
（A）17 （B）19 （C）21 （D）23
5、工人月工资
（元）依劳动生产率x（千元）变化的回归直线方程为
，下列判断正确的是
（ ）
(A)劳动生产率为1000元时，工资为50元
(B)劳动生产率提高1000元时，工资提高150元
(C)劳动生产率提高1000元时，工资提高90元
(D)劳动生产率为1000元时，工资为90元
6、在某次体育活动中，统计甲、乙两班学生每分钟跳绳的成绩（单位：次）情况如下表：
| 班级 | 参加人数 | 平均次数 | 中位数 | 方差 |
| 甲 | 55 | 135 | 149 | 190 |
| 乙 | 55 | 135 | 151 | 110 |
下面有3个命题：
（1）甲班学生的平均成绩高于乙班学生的平均成绩；
（2）甲班学生成绩的波动比乙班学生成绩的波动大；
（3）甲班学生成绩优秀人数不会多于乙班学生成绩优秀的人数（跳绳次数≧150次为优秀）。
其中正确的命题是 （ ）
（A）（1） （B）（2） （C）（3） （D）（2）（3）
7、从一批产品中取出三件产品，设A=“三件产品全不是次品”，B=“三件产品全是次品”，C=“三件产品不全是次品”，则下列结论正确的是 （ ）
（A）A与C互斥 （B）B与C互斥
（C）任何两个均互斥 （D）任何两个均不互斥
8、在5件产品中，有3件一等品，2件二等品。从中任取2件，那么以
为概率的事件是
（ ）
（A）都不是一等品 （B）恰有一件一等品
（C）至少有一件二等品 （D）至少有一件一等品
9、下列算法输出的结果是 （ ）
（A）1+3+5+…+2005；
（B）1×3×5×…×2005；
（C）求方程1×3×5×…×n=2005中的n值；
（D）满足1×3×5×…×n＞2005的最小整数n．
10、一组数据中的每一个数据都减去80得一组新数据，则这组新数据的平均数是1.2，方差是4.4，则原来一组数据的平均数和方差分别是 （ ）
（A） 81.2, 4.4 （B） 78.8, 4.4
（C） 81.2, 84.4 （D）78.8, 75.6
11、将数字1、2、3填入标号为1，2，3的三个方格里，每格填上一个数字，则方格的标号与所填的数字有相同的概率是
（ ）（A）
（B）
（C） （D）
12、正四面体的4个面上分别写着1、2、3、4，将3个这样均匀的正四面体同时投掷于桌面上，与桌面接触的3个面上的3个数的乘积能被4整除的概率是 （ ）
(A)
(B)
(C)
(D)
二、填空题：（共6题，每小题4分）
13、对划船运动员甲、乙两人在相同的条件下进行6次测试，测得他们在最大速度（m／s）的数据的茎叶图如右图所示，试问哪一位运动员较为优秀？ ．
14、在平面直角坐标系中，横坐标与纵坐标都在集合A＝{0，1，2，3，4，5}内取值的点中任取一个点，此点正好在直线
上的概率为 ．
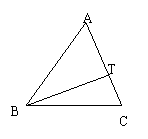
15、如下图，过正三角形ABC的顶点B任作一条射线BT，交AC于T，则CT
BC的概率为_________.
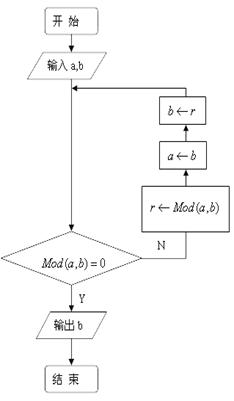
16、在右图所示的算法流程图中，若输入
，
，则输出的结果是 。[ Mod(a,b)表示a除以b所得的余数。]
17、下面的代码的执行结果是S= ，H= .
S←40
H←
For n from 2 to 5
S←S+2×H
H←
End for
Print S，H
18、数据－1，0，3，4，6，x，y的众数为x，中位数为y，平均数为x+y，则x－y=
三、解答题：（共6题，共66分）
19、有一个容量为 20 的样本，其数据如下（单位：岁） (12分)
44 45 29 42 58 37 53 52 49 34
27 32 42 55 40 38 50 26 54 26
⑴填写以下的频率分布表；
⑵绘出频率分布图和折线图（在同一幅图中作）；
⑶据频率分布图的各组中值估计总体平均数，并将所得结果与实际的总体平均数相比较，计算误差。
| 分组 | 频数 | 频率 | 频率/组距 |
| [19.5,29.5] | |||
| [29.5,39.5] | |||
| [39.5,49.5] | |||
| [49.5,59.5] | |||
| 合计 |
20、（12分）甲、乙两人约定于6时到7时之间在某地会面，并约定先到者应等候另一个人一刻钟，过时即可离去。求两人能会面的概率。
21、（10分）某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
| 商店名称 | A | B | C | D | E E |
| 销售额(x)/千万元 | 3 | 5 | 6 | 7 | 9 9 |
| 利润额(y)/百万元 | 2 | 3 | 3 | 4 | 5 |
(1) 画出销售额和利润额的散点图。
(2) 若销售额和利润额具有相关关系，试计算利润额y对销售额x的回归直线方程．
22、（10分）将甲、乙两枚骰子先后各抛一次，a、b分别表示抛掷甲、乙两枚骰子所
x>0
出的点数，若把点P(a,b)落在不等式组 y>0 所表示的平面区域的事件记为A，求P(A)
x+y≤4
23、（10分）给出30个数：1，2，4，7，……，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，依次类推。求第30个数，写出伪代码，画出流程图。
24、（12分）把编号为1，2，3的3个球随机的放入3个盒中，每盒放球数不限，求下列事件的概率：
A=“3个球在同一盒中” B=“1盒1个球”
C=“第1个球在第二盒中 D=“第1个盒恰有2个球”
高二年级数学第一学期期中考试
试题参考答案
一、选择题：
1、D 2、B 3、B 4、A 5、C 6、D 7、D 8、C 9、D 10、A 11、D 12、B
二、填空题：
13、乙 14、 15、 16、17 17、115 
18、-2
三、解答题：
(1)
| 分组 | 频数 | 频率 | 频率/组距 |
| [19.5,29.5] | 4 | 0.2 | 0.02 |
| [29.5,39.5] | 4 | 0.2 | 0.02 |
| [39.5,49.5] | 6 | 0.3 | 0.03 |
| 49.5,59.5] | 6 | 0.3 | 0.03 |
| 合计 | 20 | 1 | 0.1 |
(2)
频率/组距
0.03
 |
0.02
19.5 39.5 9.5
(3)组中值估计总体平均数为:41.5 实际的总体平均数: 41.65
误差:0.15
20、以x和y分别表示甲、乙两人到达约会地点的时间，则两人能够会面的条件是x-y≤15。在平面上建立直角坐标系，则（x，y）的所有基本事件可以看作是边长为60的正方形，则可能会面的时间由图中的阴影部分所表示，故P（两人能会面）=
=
答：两人能会面的概率为
21、（1）略
（2）
b=
a=
利润额y对销售额x的回归直线方程: 
+
22、解：总共有基本事件36种，事件A包含基本事件有（1，1），（1，2），（1，3），（2，1），（2，2），（3，1）6种，所以P（A）=
23、
|
|
| ||||||
24、解：所有的基本事件为27个，事件A、B、C、D分别包含3、6、9、6个基本事件，所以它们的概率P（A）=
、P（B）=
、P（C）=、P（D）=