《圆的方程》检测题
.
一、选择题(每小题5分,12个小题共60分)
1.经过点A(5,2),B(3,2),圆心在直线2x─y─3=0上的圆的方程为 ( )
![]() (x-4)2+(y-5)2=10
(x-4)2+(y-5)2=10 ![]() (x+4)2+(y-5)2=10
(x+4)2+(y-5)2=10 ![]() (x-4)2+(y+5)2=10
(x-4)2+(y+5)2=10 ![]() (x+4)2+(y+5)2=10
(x+4)2+(y+5)2=10
2.以O(0,0),A(2,0),B(0,4)为顶点的三角形OAB外接圆的方程为 ( )
![]() x2+y2+2x+4y=0
x2+y2+2x+4y=0 ![]() x2+y2-2x-4y=0
x2+y2-2x-4y=0 ![]() x2+y2+2x-4y=0
x2+y2+2x-4y=0 ![]() x2+y2-2x+4y=0
x2+y2-2x+4y=0
3.已知方程x2+y2-2(m+3)x+2(1─
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4.过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点,且面积最小的圆方程为 ( )
![]() (x+13/5)2+(y+6/5)2=4/5
(x+13/5)2+(y+6/5)2=4/5
![]() (x-13/5)2+(y-6/5)2=4/5
(x-13/5)2+(y-6/5)2=4/5
![]() (x-13/5)2+(y+6/5)2=4/5
(x-13/5)2+(y+6/5)2=4/5
![]() (x+13/5)2+(y-6/5)2=4/5
(x+13/5)2+(y-6/5)2=4/5
5.圆C与直线![]() :2x-2
:2x-2![]() y-1=0切于P(
y-1=0切于P(![]() ,
,![]() ),且过点Q(
),且过点Q(![]() ,2
,2![]() ),则该圆的方程为( )
),则该圆的方程为( )
![]() x2+y2-2x
-5
x2+y2-2x
-5![]() y+
y+![]() =0
=0
![]() x2+y2-2x
+5
x2+y2-2x
+5![]() y+27=0
y+27=0
![]() x2+y2+2x
-5
x2+y2+2x
-5![]() y+
y+![]() =0
=0
![]() x2+y2-2x
-5
x2+y2-2x
-5![]() y+27=0
y+27=0
6. 方程![]() 表示的曲线是
( )
表示的曲线是
( )
![]() 都表示一条直线和一个圆
都表示一条直线和一个圆
![]() 都表示两个点
都表示两个点
![]() 前者是一条直线和一个圆,后者是两个点
前者是一条直线和一个圆,后者是两个点 ![]() 前者是两个点,后者是一直线和一个圆
前者是两个点,后者是一直线和一个圆
7.到一个三角形的三个顶点的距离的平方和最小的点,是这个三角形的 ( )
![]() 垂心
垂心
![]() 重心
重心
![]() 外心
外心
![]() 内心
内心
8.设![]() 是曲线C:
是曲线C:![]() 为参数,
为参数,![]() )上任意一点,则
)上任意一点,则![]() 的取值范围是
的取值范围是
( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
9.方程![]() 有两个不等实根,则k的取值范围是 ( )
有两个不等实根,则k的取值范围是 ( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
10.圆![]() (a≠0,θ为参数)的圆心的轨迹方程是( )
(a≠0,θ为参数)的圆心的轨迹方程是( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
11.同心圆:![]() 与
与![]() ,从外圆上一点作内圆的两条切线,则两条切线的夹角为( )
,从外圆上一点作内圆的两条切线,则两条切线的夹角为( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
12.一辆卡车宽
![]()
![]()
![]()
![]()
二、填空题(本大题共4小题,每小题4分,共16分)
13.圆x2+y2+2x+4y-3=0上到直线4x-3y=2的距离为 ![]() 的点数共有 .
的点数共有 .
14.与圆![]() 外切,且与直线x+1=0相切的动圆圆心的轨迹方程是_______
._
外切,且与直线x+1=0相切的动圆圆心的轨迹方程是_______
._
15.设集合m={(x,y)x2+y2≤25},N={(x,y)|(x-a)2+y2≤9},若M∪N=M,则实数a的取值范围是 .
16.直线![]() x+y-2
x+y-2![]() =0截圆x2+y2=4得的劣弧所对的圆心角的弧度数为
.
=0截圆x2+y2=4得的劣弧所对的圆心角的弧度数为
.
圆的方程检测题(A卷)
班级 学号 姓名 得分
一.选择题(每小题5分,12个小题共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二.填空题(每小题4分,4个小题共16分)
13. 14.
15. 16.
三.解答题(第17、18、19、20、21小题每小题12分, 第22小题14分,6个小题共74分)
17.求经过点![]() ,和直线
,和直线![]() 相切,且圆心在直线
相切,且圆心在直线![]() 上的圆方程.
上的圆方程.
18.已知圆C:(x+4)2+y2=4和点A(-2![]() ,0),圆D的圆心在y轴上移动,且恒与圆C外切,设圆D与y 轴交于点M、N. ∠MAN是否为定值?若为定值,求出∠MAN的弧度数;若不为定值,说明理由.
,0),圆D的圆心在y轴上移动,且恒与圆C外切,设圆D与y 轴交于点M、N. ∠MAN是否为定值?若为定值,求出∠MAN的弧度数;若不为定值,说明理由.
19.求圆x2+y2=4 和(x-4)2+y2=1的外公切线的方程及外公切线段的长度.
20.已知直线![]() :y=k (x+2
:y=k (x+2![]() )与圆O:
)与圆O:![]() 相交于A、B两点,O是坐标原点,三角形ABO的面积为S.
相交于A、B两点,O是坐标原点,三角形ABO的面积为S.
(1)试将S表示成的函数S(k),并求出它的定义域;
(2)求S的最大值,并求取得最大值时k的值.
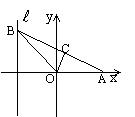
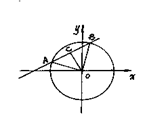
21.如图,给定点A(![]() ,0)(
,0)(![]() >0)和直线l:x+1=0,B为l上的动点,
>0)和直线l:x+1=0,B为l上的动点,![]() 的平分线交AB于点C,求点C的轨迹方程.
的平分线交AB于点C,求点C的轨迹方程.
22.已知圆M:2x2+2y2-8x-8y-1=0和直线l:x+y-9=0 . 过直线l 上一点A作△ABC,使
∠BAC=45°,AB过圆心M,且B,C在圆M上.
⑴当A的横坐标为4时,求直线AC的方程;
⑵求点A的横坐标的取值范围.
圆的方程检测题(A卷)参考答案
一、选择题
二、填空题 13.4个. 14.![]() 15.-2≤a≤2 16.
15.-2≤a≤2 16. ![]()
三.解答题
17. 【解】:![]()
18. 【解】设圆D的方程为![]() 那么
那么![]()
因为圆D与圆C外切, 所以![]()
又直线![]() 的斜率分别为
的斜率分别为 ![]()
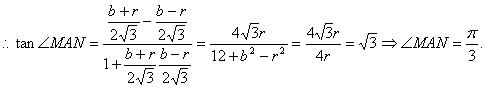 为定值
为定值
19.【解】:圆x2+y2=4 和(x-4)2+y2=1的圆心分别为O(0,0),C(4,0), 设两圆的连心线与外公切线交于点P(x0,0),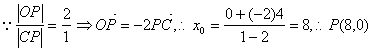 .
.
由此可设两圆的外公切线方程为![]() 即
即![]() 圆O的圆心到这切线的距离
圆O的圆心到这切线的距离
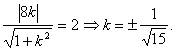
![]() 两圆的外公切线方程为
两圆的外公切线方程为![]() ,即
,即
![]() ,和
,和![]()
外公切线段的长![]()
20.【解】::如图,
 (1)直线
(1)直线![]() 议程
议程 ![]()
原点O到![]() 的距离为
的距离为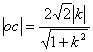
弦长![]()
△ABO面积![]()
![]()
![]()
![]()
(2) 令
![]()
![]() 当t=
当t=![]() 时,
时, ![]() 时,
时, ![]()
又解:△ABO面积S=![]()
![]()
![]()
此时![]()
即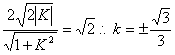
21. 【解】:设![]() ,
,![]()
![]() 又设
又设![]() ,
,![]()
![]()
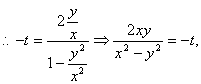 ……①
……①
又因为A、C、B三点共线, 所以
![]() ……② 由①、②得
……② 由①、②得![]()
![]() ,
,![]() ,化简整理得点C的轨迹方程为
,化简整理得点C的轨迹方程为 ![]()
22.【解】:⑴依题意M(2,2),A(4,5),![]() ,设直线AC的斜率为
,设直线AC的斜率为![]() ,则
,则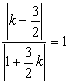 ,解得
,解得![]() 或
或![]() ,故所求直线AC的方程为5x+y-25=0或x-5y+21=0;
,故所求直线AC的方程为5x+y-25=0或x-5y+21=0;
⑵圆的方程可化为(x-2)2+(y-2)2=![]() ,设A点的横坐标为a。则纵坐标为9-a;
,设A点的横坐标为a。则纵坐标为9-a;
①
当a≠2时,![]() ,设AC的斜率为k,把∠BAC看作AB到AC的角,
,设AC的斜率为k,把∠BAC看作AB到AC的角,
则可得![]() ,直线AC的方程为y-(9-a)=
,直线AC的方程为y-(9-a)=![]() (x-a)
(x-a)
即5x-(
又点C在圆M上,所以只需圆心到AC的距离小于等于圆的半径,即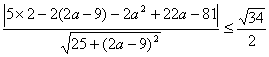 ,化简得a2-
,化简得a2-
②当a=2时,则A(2,7)与直线 x=2成45°角的直线为y-7=x-2即x-y+5=0,
M到它的距离![]() ,这样点C不在圆M上,还有x+y-9=0,显然也不满足条件,故A点的横坐标范围为[3,6]。
,这样点C不在圆M上,还有x+y-9=0,显然也不满足条件,故A点的横坐标范围为[3,6]。