高二（上）期末数学复习自测卷(三套）

高二（上）期末数学复习自测卷（1）

一．选择题 : 本大题共12小题, 每小题3分, 共36分. 在每小题给出的四个选项中, 有且只有一项是符合题目要求的 .

1．已知集合M = {x x – 2 < 3, 且x Î Z}，则集合M中元素的个数是（A）7（B）6　　（C）5　（D）4（　　）

2．双曲线的焦点坐标是 (A)（– 2，0），（2，0）.　 (B)（0，– 2），（0，2）.(C)（0，– 4），（0，4）. (D)（– 4，0），（4，0）（　　　）

3. 直线x – 2y +2 = 0与直线3x – y + 7 = 0的夹角等于 (A).　(B).　(C).　(D) arctan7.　(　　 )

4. 不等式 > 的解集是(A) {x x ¹ –1}.　　(B) { x x > –1 }.　 (C) { x x < 0且x ¹ –1 }.　(D){x –1 < x < 0 } ( 　 )

5. 若椭圆两准线间的距离是焦距的4倍，则该椭圆的离心率为 （A）.　（B）.　 （C）.（D）.（　　）

6. 已知两点A( –2, 0 ) , B( 0 , 2 ), 点P是椭圆=1上任意一点，则点P到直线AB距离的最大值是 （　　）

　 (A) .　(B) 3.　　(C) .　 (D) 0.  

7．直线y = x + 1被椭圆=1所截得的弦的中点坐标是(A) (,).  (B) (,).　(C) (–,). (D)( –, –) (　　　).

8. 如果实数x、y满足x + y = 4，则x² + y²的最小值是　 (A)4　 (B)6.　 (C)8.  (D)10. (　　)

9. 在相距4k米的A、B两地, 听到炮弹爆炸声的时间相差2秒, 若声速每秒k 米, 则爆炸地点P必在　(　　　)　

(A) 以A，B为焦点, 短轴长为k米的椭圆上 .(B) 以AB为直径的圆上.

(C) 以A，B为焦点, 实轴长为2k米的双曲线上 .(D) 以A，B为顶点, 虚轴长为k米的双曲线上.

10. “a + b > 4”成立的一个充分不必要条件是 (A) a > 2或b > 2.　(B) a > 2或b < 2.　 (C) a > 2且 b > 2.  (D) a > 2且b < 2（　　 ）

11. 已知曲线C₁: y= –x ² +4x–2 , C₂: y ² = x, 若C₁、C₂ 关于直线l对称, 则l的方程是　(　　)　 (A) x + y + 2 = 0.　 (B) x + y –2 = 0. 　　(C) x – y + 2 = 0. 　 (D) x – y – 2 = 0.

12．已知 – 1< x + y < 3，且2 < x – y < 4，则2x +3y的取值范围是 (　　 )

（A）（–，）　（B）（–，）　（C）（–，）　（D）（–，）

二．填空题：本大题有4小题, 每小题4分, 共16分. 请将答案填写在答题卷中的横线上.

13．已知a ÎR⁺, 且a ≠ 1,　又M = , N = , P = , 则M, N , P的大小关系是 　　　　　　　　 .

（第15题）

14. 在平面直角坐标系内， 动点P到x轴、y轴的距离之积等于1， 则点P的轨迹方程是 　　　　　　　　　  .

15. 如图, 直线l ^ FH于H, O为FH的中点, 曲线C₁ , C₂是以F为焦点, l为准线的圆锥曲线(图中只画出曲线的一部分）, 那么圆锥曲线C₁是 　　　　　　; 圆锥曲线C₂是 　　　　　　 .

16. 一次化学实验中需要用天平称出20g氧化铜粉末, 某同学发现自己所用的天平是不准的(其两臂不等长)，因此, 他采用了下列操作方法：选10g的法码放入左盘, 置氧化铜粉末于右盘使之平衡，取出氧化铜粉末, 然后又将10g法码放于右盘, 置氧化铜粉末于左盘, 平衡后再取出.  他这样称两次得到的氧化铜粉末之和应该

　　　　　　　  20g. (选用“大于”，“小于”，“等于”，“不小于”，或“不大于”填空 )

三．解答题：本大题有4小题, 共48分. 解答应写出文字说明, 证明过程或演算步骤.

17．(满分10分)已知直线l满足下列两个条件：(1) 过直线y = – x + 1和y = 2x + 4的交点; (2)与直线x –3y + 2 = 0 垂直，求直线l的方程.

18. (本小题满分12分)已知A =, B = x + 1, 当x ≠ 1时，试比较A与B的大小, 并说明理由.

19. (本小题满分14分)

已知抛物线 y ² = – x与直线 y = k ( x + 1 )相交于A、B两点, 点O是坐标原点.

(1) 求证: OA^OB;　

(2) 当△OAB的面积等于时, 求k的值.

20. (本小题满分12分)

某游泳馆出售学生游泳卡，每张240元，使用规定：不记名，每卡每次只限1人，每天只限一次. 某班有48名学生, 老师打算组织同学们集体去游泳, 且要求每位学生能游8次.在费用开支方面, 除需购买x张游泳卡外, 每天游泳还要包一辆汽车, 无论乘坐多少名学生. 每次包车费均为40元.  

（1）试写出游泳活动总开支y元关于购买游泳卡张数x 的函数解析式；

（2）试求出购买多少张游泳卡，可以使每位同学需要交纳的费用最少? 最少需要交多少元?

21 附加题: (本题分值6分, 计入总分, 但本题与必做题得分之和不超过100分.)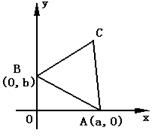

（附加题）

已知a , b都是正数，△ABC是平面直角坐标系xOy内, 以两点A ( a , 0 )和B ( 0 , b )为顶点的正三角形，且它的第三个顶点C在第一象限内.

（1）若△ABC能含于正方形D = { ( x , y ) 0 £ x £ 1, 0£ y £ 1}内， 试求 变量 a , b 的约束条件，并在直角坐标系aOb内（见答题卷）内画出这个约束等条件表示的平面区域；

（2）当( a, b )在（1）所得的约束条件内移动时，求△ABC面积S的最大值，并求此时（a , b ）的值.

高二（上）期末数学复习自测卷（2）

一、选择题（3×12=36分）

1、若a、b为任意实数,且a>b，则

A) a²>b²　　　　B) <1　　　  C)lg(a-b)>0　　　 D)<

2、下列不等式：（1）；（2）（a、b∈R⁺）；

（3）；（4）（a、b∈R⁺）；其中不正确的有

A)　0个　　　 B)　1个　　　　C) 2个　　　　  D)　3个

3、对直线3x-2y+6=0的描述，正确地是

A) 横纵截距分别为-2和3　　　　　　  B) 原点到直线的距离为　

C) 与直线4x+6y-7=0互相平行　　　　  D) 倾斜角为锐角，斜率为

4、下列不能表示平行于x轴的直线方程形式是

A） 点斜式　　 B） 斜截式　　 C）截距式　　　　  D）一般式

5、与直线x-y-2=0平行且与它的距离等于的直线方程为

A）x-y=0 　　　　 B）x-y+6=0或x-y-2=0

C)x-y-2=0 　　　　 D)x-y-6=0或x-y+2=0

6、两圆x²+y²-6x+4y+12=0和x²+y²-14x-2y+14=0的位置关系是

A）相交　　　B）内切　　　 C） 外切　　　　 D）内含

7、方程表示的图形是

A） 半个圆　　 B） 一个椭圆　 C） 双曲线的一支　  D）一个圆

8、椭圆+=1上一点P与两焦点F₁、F₂的连线互相垂直，则ΔPF₁F₂的面积

A） 20　　　　 B） 22　　　　C） 28　　　　　  D） 24

9、椭圆上一点M到准线的距离与它到对应于该准线的焦点距离之比为

A） 　　　　 B） 　　　　C） 　　　　　D）

10、参数方程所表示的曲线是

A） 以为焦点的椭圆　　　 B） 以(±5，0)为焦点的椭圆　

C） 离心率为的椭圆　　　　　　 D）离心率为的椭圆

11、过抛物线y²＝4x的焦点作一条直线交抛物线于A(x₁，y₁)，B(x₂，y₂)两点，如果x₁＋x₂＝8，那么AB＝

A） 12　　　　 B）10　　　　 C）8　　　　　 D）4

12、双曲线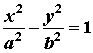 (0<a<b)的半焦距为c，直线L过两点(a , 0),(0 , b)，且双曲线的中心到直线L的距离为，则双曲线的离心率为

A） 2 　　　 B） 　　　C） 　　　D）

二、填空题（3×4=12分）

13、不等式的解集是______________________；

14、经过直线4x+3y－7=0和5x+3y－8=0的交点，且倾斜角是135°的直线的横截距为________________________________；

15、方程(3m+4)x+(5－2m)y+7m－6=0表示的曲线恒过一定点，其坐标为_______；

16、若xÎ(0，2)，则f(x)=的最大值为_______，此时x的值为_______；

三、解答题（10+10+10+10+12=52分）

17、设z=2x+y，且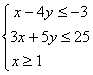，求z的最大值和最小值。

18、求过直线x-3y+3=0与2x-y-4=0的交点，圆心在直线y=2x上，且与直线y=2x+5相切的圆的方程。

19、双曲线与椭圆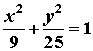共焦点，且其渐近线方程为，求该双曲线方程并写出它的准线方程和范围。

20、抛物线y²＝－2px　(p>0)上有一点M横坐标为－9，它到焦点的距离等于10，求抛物线的标准方程及M点的坐标。

21、在△ABC中，B、C两点间距离为6，点A到两点B、C距离的平方和为26；

(1)　  求点A的轨迹方程；

(2)  判断直线x－2y＋2＝0与该曲线的位置关系，如果相交，求出弦长。

高二（上）期末数学复习自测卷（3）

一．选择题（每题5分）

1、直线A x+B y+C=0 (A ²+B ²≠0)是一、三象限角平分线的充要条件是（　 ）

A  A=1，B=-1　　　　 B A=B≠0，C=0　

 C A+B=0，C=0　　　　D 以上均不正确

2、曲线（为参数）上的点到原点的最大距离为（　 ）

A 1　　　　　　 B 　　　　　　 C 2　　　　　　　　 D 4

3、通过水管放水，当流速相同时，如果水管截面（指横截面，下同）的内径周长为4cm，单位时间内截面是圆的水管比截面是正方形的水管流量（　 ）

A  大　 　　B 大　　 C 小　　 D 相等

4、若点P（1，2）在椭圆x ²+ a y ²—5 a = 0（a＞0且a≠1）内部，则a 的取值范围是（　 ）

A　0＜a＜1　　 B　0＜a＜2且a≠1　　 C　1＜a＜2　　　D　a＞1

_{5、已知点A、B分别在x轴、y轴上滑动，且 AB = a，则线段AB的中点轨迹为（　 ）}

A  x ²+y ²= a ² B  x ²+y ²=　　 C  x +y-a=0　　D　x +y-2a=0

6、若点P（x₀，y₀）不在直线l：A x+B y+C=0上，则过P且与l平行的直线方程为（　 ）

A  A x+B y+（x₀+y₀）=0　　　　　 B　 A x+B y+Ax₀+By₀=0

C  A x+B y--Ax₀--By₀=0　　　　　  D　 A x+B y--（x₀+y₀）=0

7、已知P是椭圆上一点，F₁、F₂是椭圆的两个焦点，若∠P F₁F₂=60⁰，∠P F₂ F₁=30⁰，则该椭圆的离心率为（　 ）

A 　　　　 B 　　　　　C 　　　　　D

8、若P（x₀，y₀）在直线A x+B y+C=0(A＞0)右方，则P到直线A x+B y+C=0的距离d=（　 ）

A 　　　　　　　　 B —

C  D

9、设x , y均为正数，则（x +y）² +的最小值为（　 ）

A 2　　　　　 B 4　　　　 C 8　　　　　 D 16

10、的最大值为（ 　）

A　　　　　B 　　　　　C 　　　　　D

二．填空题（每题4分） 

11．不等式组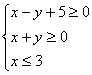表示的区域面积为_{——————————}。

12．若z=7 x+25 y，式中x、y满足约束条件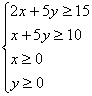，则z的最小值为　　　　。

13．P(—11，2)的光线射到x轴，反射光线恰与圆x ² +（y—1）²= 13相切，求入射光线所在直线方程　　　　　  。

14．线x ²+y ²= x + y 上的点到直线x +y —1=0的最大距离为　　 。

15．曲线y=1+（x∈[—2，2]）与直线y=k（x-2）+4有两个公共点时，则k的取值范围是　　　　。

三．解答题：

　16．（8分）平行四边形两条边所在直线方程为x+y-1=0,3x-y+4=0,它的对角线交点为M（3，3），求这个平行四边形另两条边所在直线方程。

17．（10分）已知：圆的方程x²+(y-1)²=4,过点A（0，3）作圆的割线交圆与点P，求线段AP中点的轨迹。

18．（10分）证明不等式：a²+b²+1ab+a+b

19．（10分）已知：P为椭圆x²+a²y²=a²(a>1)上一动点，定点A（0，-1），

求 AP _max

20．（12分）设圆满足：（1）截y 轴所得弦长为2；（2）被x轴分成两段圆弧，其弧长比为3：1，在满足（1）（2）的所有圆中，求圆心到直线l：x—2y=0的距离最小的圆的方程。