高二(下)数学中期模拟考试题(1)
一.选择题(本大题共12小题,每小题5分,共60分)
1.已知向量a=(1,1,0),b=(-1,0,2),且![]() a+b与
a+b与![]() 的值是( )
的值是( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
2.若n∈N*,则(20-n)(21-n)……(100-n)等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、![]() ,
,![]() 表示两个不同的平面,
表示两个不同的平面,![]() ,
,![]() 表示两条不同的直线,则
表示两条不同的直线,则![]() //
//![]() 的一个充分不必要条件是
的一个充分不必要条件是
A.![]() //
//![]() ,
,![]() ,
,![]() B.
B.![]() //
//![]() ,
,![]() //
//![]() ,
,![]() //
//![]()
C.![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() //
//![]() D.
D.![]() //
//![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
4、从4位男教师和3位女教师中选出3位教师,派往郊区3所学校支教,每校1人.要求这3位教师中男、女教师都要有,则不同的选派方案共有 ( )
A.210种 B.186种 C.180种 D.90种
5.已知A、B、C三点不共线,对平面ABC外的任一点O,下列条件中能确定点M与点A、B、C一定共面的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.已知直线l⊥平面a,直线m![]() 平面
平面![]() ,有下面四个命题:
,有下面四个命题:
① ![]() ∥β
∥β![]() l
l![]() m
②
m
② ![]() ⊥β
⊥β![]() l∥m
l∥m
③ l∥m![]()
![]() ⊥β
④ l⊥m
⊥β
④ l⊥m![]()
![]() ∥β
∥β
其中正确的两个命题是
A.①与② ③与④ .②与④ .①与③
7.二面角α—EF—β是直二面角,C∈EF,AC ![]() α,BC
α,BC![]() β,∠ACF=30°,
β,∠ACF=30°,
∠ACB=60°,则cos∠BCF等于( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
8.把∠A=60°,边长为a的菱形ABCD沿对角线BD折成60°的二面角,则AC与BD的距离为( )
A.![]() a B.
a B.![]() a C.
a C.![]() a D.
a D.![]() a
a
9.长方体一个顶点上的三条棱长分别是3、4、5,且它的8个顶点都在同一个球面上,则这个球的表面积是( )
A. ![]() B.
B.![]() C.
C.![]() D.
D. ![]()
10.设A、B、C、D是空间不共面的四点,且满足![]() ,则△BCD是 (
)
,则△BCD是 (
)
A.钝角三角形 B.直角三角形 C.锐角三角形 D.不确定
11.在北纬60°圈上有A、B两地,它们的纬线圈上的劣弧长等于![]() (R为地球半径),则这两点的球面距离是
(R为地球半径),则这两点的球面距离是
A. ![]() B.
B.![]() C.
C.![]() D. 2R
D. 2R
12.(文科)在棱长为1的正方体ABCD—A1B
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(理科)已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,则点B到平面EFG的距离为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
二.填空题(本大题4小题,每小题4分,共16分)
13.已知向量a=(![]() +1,0,2
+1,0,2![]() ),b=(6,2
),b=(6,2![]() -1,2),若a∥b,则
-1,2),若a∥b,则![]() 与
与![]() 的值分别是
.
的值分别是
.
14.若![]() , 则n的值为 .
, 则n的值为 .
15..由0,1,2,3,4,5可以组成奇数与偶数相间且能被5整除的无重复数字的六位数的个数是 。
16.下面是关于四棱柱的四个命题:
①若有两个侧面垂直于底面,则该四棱柱为直四棱柱
②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱
③若四个侧面两两全等,则该四棱柱为直四棱柱
④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱
其中,真命题的编号是 (写出所有正确结论的编号).
三.解答题(本大题6小题,共74分)
 17.(本小题满分12分)
17.(本小题满分12分)
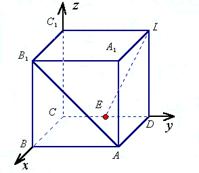
如图,在棱长为2的正方体ABCD-A1B
(1)写出A、B1、E、D1的坐标;
(2)求AB1与D1E所成的角的余弦值.
18、.(本小题满分12分)
设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入5个盒子内
(1)只有一个盒子空着,共有多少种投放方法?
(2)没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?
(3)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
 19
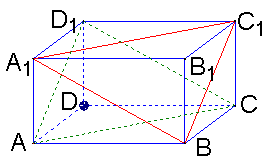
19![]() 在长方体ABCD—A1B
在长方体ABCD—A1B![]()
(1) 求平面A1BC1与平面ACD1间的距离;
(2)
求点B1到平面A1BC1的距离![]()
20.(本小题满分12分)
 如图,在直三棱柱ABC—A1B
如图,在直三棱柱ABC—A1B
(1)求异面直线AD与A1B1所成角的余弦值;
(2)试在线段AB上找一点E,使得:A1E⊥AD;
19.(本小题满分12分)
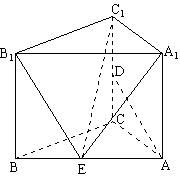
如图,在四棱锥![]() 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱![]() 底面ABCD,
底面ABCD,
|
(1)证明 ![]() 平面
平面![]() ;
;
(2)证明![]() 平面EFD.
平面EFD.
22.(本题14分)
注:文科做(1)(2)理科做(1)(2)(3)
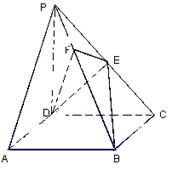
如图,四棱锥P—ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
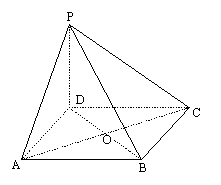 (1)求证:平面PAC⊥平面PBD;
(1)求证:平面PAC⊥平面PBD;
(2)求PC与平面PBD所成的角;
(3)在线段PB上是否存在一点E,
使得PC⊥平面ADE?若存在,请加
以证明,若不存在,请说明理由。