高二《曲线方程和圆》单元测试卷
班级: 考号: 姓名:
一、选择题(本大题共10小题,每小题5分,共50分)
1.到两坐标轴的距离之和为6的点的轨迹方程是 ( )
A.x+y=6 B.x±y =
2.原点必位于圆:![]()
![]() 的 ( )
的 ( )
A.内部 B.圆周上 C.外部 D.均有可能
3.平行四边形ABCD的一条对角线固定在A(3,-1),C(2,-3)两点,D点在直线3x-y+1=0上移动,则B点轨迹所在的方程为 ( )
A.3x-y-20=0 B.3x-y-10=
4.“点M在曲线y=|x|上”是“点M到两坐标轴距离相等”的 ( )
A.充要条件 B.必要不充分条件 C.充分不必要条件 D.非充分非必要条件
5.从动点![]() 向圆
向圆![]() 作切线,其切线长的最小值是 ( )
作切线,其切线长的最小值是 ( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.若曲线x2+y2+a2x+(1–a2)y–4=0关于直线y–x=0的对称曲线仍是其本身,则实数a=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.直线y
= x + b与曲线x=![]() 有且仅有一个公共点,则b的取值范围是 ( )
有且仅有一个公共点,则b的取值范围是 ( )
A.b=![]() B.
B.![]()
C.![]() D.以上都错
D.以上都错
8.圆![]() 上到直线3 x + 4y -11=0的距离等于1的点有 ( )
上到直线3 x + 4y -11=0的距离等于1的点有 ( )
A.1个 B.2个 C.3个 D.4个
![]() 9.已知圆C:
9.已知圆C: ![]() (a>0,
(a>0,![]() )及直线
)及直线![]() :
:![]() ,若直线
,若直线![]() 被C截得
被C截得
的弦长为![]() ,则
,则![]() =
( )
=
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若圆![]() 上至少有三个不同点到直线
上至少有三个不同点到直线![]() :
:![]() 的距离为
的距离为![]() ,则直线
,则直线![]() 的倾斜角的取值范围是
( )
的倾斜角的取值范围是
( )
A.[![]() ]
B.[
]
B.[![]() ]
C.[
]
C.[![]() D.
D.![]()
二、填空题(本大题共5小题,每小题5分,共25分)
11.若直线y=kx+2与圆(x-2)2+(y-3)2=1有两个不同的交点,则k 的取值范围是 。
12.过P(1,2)的直线l把圆![]() 分成两个弓形当其中劣孤最短时直线
分成两个弓形当其中劣孤最短时直线![]() 的方程为
____ 。
的方程为
____ 。
13.已知直线![]() 与圆
与圆![]() 相切,则
相切,则![]() 的值为
。
的值为
。
14.已知BC是圆![]() 的动弦,且BC=6,则BC的中点的轨迹方程是 ______。
的动弦,且BC=6,则BC的中点的轨迹方程是 ______。
15.已知圆M:(x+cosq)2+(y-sinq)2=1,直线l:y=kx,下面四个命题:
①对任意实数k与q,直线l和圆M相切;
②对任意实数k与q,直线l和圆M有公共点;
③对任意实数q,必存在实数k,使得直线l与和圆M相切
④对任意实数k,必存在实数q,使得直线l与和圆M相切
其中真命题的代号是______________(写出所有真命题的代号)。
三、解答题(本大题共6小题,共75分)
16.若M为直线![]() 上的一点,A(4,2)为一定点,又点P在直线AM上运动,且
上的一点,A(4,2)为一定点,又点P在直线AM上运动,且![]() 求动点P的轨迹方程.(12分)
求动点P的轨迹方程.(12分)
17.求与直线 y=x 相切,圆心在直线 y=3x上且被
y 轴截得的弦长为![]() 的圆的方程.(12分)
的圆的方程.(12分)
18.自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线m所在直线与圆C:x 2 + y 2 -4x-4y +7 = 0相切,求光线L、m所在的直线方程.(12分)
19.已知圆![]() 与y轴交于A、B两点,圆心为P,若
与y轴交于A、B两点,圆心为P,若![]() .
.
求m的值.(12分)
20.设圆![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(1)求![]() 关于
关于![]() 对称的圆
对称的圆![]() 的方程;
的方程;
(2)当![]() 变化且
变化且![]() 时,求证:
时,求证:![]() 的圆心在一条定直线上,并求
的圆心在一条定直线上,并求![]() 所表示的一系列圆的公切线方程.(13分)
所表示的一系列圆的公切线方程.(13分)
21.已知圆C:![]() ,是否存在斜率为1的直线L,使L被圆C截得的弦AB为直径的圆过原点,若存在求出直线L的方程,若不存在说明理由.(14分)
,是否存在斜率为1的直线L,使L被圆C截得的弦AB为直径的圆过原点,若存在求出直线L的方程,若不存在说明理由.(14分)
高二《曲线方程和圆》单元测试卷参考答案
一、选择题(本大题共10小题,每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | A | C | B | B | B | C | C | B |
10.(06年湖南卷).解:圆![]() 整理为
整理为![]() ,∴圆心坐标为(2,2),半径为3
,∴圆心坐标为(2,2),半径为3![]() ,要求圆上至少有三个不同的点到直线
,要求圆上至少有三个不同的点到直线![]() 的距离为
的距离为![]() ,则圆心到直线的距离应小于等于
,则圆心到直线的距离应小于等于![]() ,
∴
,
∴ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,![]() ,∴
,∴ ![]() ,直线
,直线![]() 的倾斜角的取值范围是
的倾斜角的取值范围是![]() ,选B.
,选B.
二、填空题(本大题共5小题,每小题5分,共25分)
11.(0,![]() ) 12.
) 12.![]() 13.-18或8 14.
13.-18或8 14. ![]() 15. ②④
15. ②④
11.(06湖北文科13题)解:由直线y=kx+2与圆(x-2)2+(y-3)2=1有两个不同的交点可得直线与圆的位置关系是相交,故圆心到直线的距离小于圆的半径,即![]() <1,解得kÎ(0,
<1,解得kÎ(0,![]() )
)
13.(06年湖北理科13题)解:圆的方程可化为![]() ,所以圆心坐标为(1,0),半径为1,由已知可得
,所以圆心坐标为(1,0),半径为1,由已知可得![]() ,所以
,所以![]() 的值为-18或8。
的值为-18或8。
15.(06年江西卷)解:选②④圆心坐标为(-cosq,sinq),
d=![]()
三、解答题(本大题共6题,共75分)
16.(12分)
[解析]:设点M,P的坐标分别为![]() ,由题设及定比分点坐标公式得
,由题设及定比分点坐标公式得
![]()
![]()
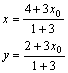
![]()
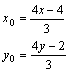 ,因为点
,因为点![]() 在直线2x-y+3=0上,所以
在直线2x-y+3=0上,所以
![]() ,即动点P的轨迹方程为:
,即动点P的轨迹方程为:![]() .
.
17.(12分)
[解析]:设圆心坐标为![]() ,则
,则![]()
![]() ,又
,又![]()
![]() ,
,![]()
即圆的方程为:![]() .
.
18.(12分)
[解析1]:.已知圆的标准方程是![]() 它关于x轴
它关于x轴
的对称圆的方程为 ![]() 设光线L所在的直
设光线L所在的直
线方程是y-3=k(x+3),由题设知对称圆的圆心![]() 到这条直线
到这条直线
的距离为1,即![]() 解得
解得
![]() .故所求入射光线L所在的直线方程为:
.故所求入射光线L所在的直线方程为:
![]() 。这时反射光线所在直线的
。这时反射光线所在直线的
斜率为![]() ,所以所求反射光线m所在的直线方程为:
,所以所求反射光线m所在的直线方程为:
3x-4y-3=0或4x-3y+3=0.
[解析2]:已知圆的标准方程是![]() 设光线L所在的直线方程是y-3=k(x+3),由题设知
设光线L所在的直线方程是y-3=k(x+3),由题设知![]() ,于是L的反射点的坐标是
,于是L的反射点的坐标是![]() ,由于入射角等于反射角,所以反射光线m所在的直线方程为:
,由于入射角等于反射角,所以反射光线m所在的直线方程为:![]() ,这条直线应与已知圆相切,故圆心到直线的 距离为1,即
,这条直线应与已知圆相切,故圆心到直线的 距离为1,即![]() 以下同解析1.
以下同解析1.
19.(12分)
[解析]:由题设△APB是等腰直角三角形,∴圆心到y轴的距离是圆半径的![]() 倍,将圆方程
倍,将圆方程
![]() 配方得:
配方得:![]() .
.
圆心是P(2,-1),半径r=![]() ∴
∴![]() 解得m= -3.
解得m= -3.
20.(13分)
[解析]:(1)圆C1的圆心为C1(-2,
设C1关于直线![]() 的对称点为C2(a,b)则
的对称点为C2(a,b)则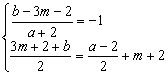 解得:
解得:![]()
∴圆C2的方程为![]()
(2)由![]() 消去m得a-2b=0, 即圆C2的圆心在定直线:x-2y=0上.
消去m得a-2b=0, 即圆C2的圆心在定直线:x-2y=0上.
设直线y=kx+b与圆系中的所有圆都相切,则![]()
即![]()
∵直线y=kx+b与圆系中的所有圆都相切,所以上述方程对所有的m![]() 值都成立,所以有:
值都成立,所以有:
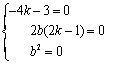
![]()
![]() ,所以
,所以![]() 所表示的一系列圆的公切线方程为:
所表示的一系列圆的公切线方程为:![]() .
.
类似地,当直线x=a与圆系中的所有圆都相切时,可以得到a=0 。
∴![]() 所表示的一系列圆的公切线方程为:
所表示的一系列圆的公切线方程为:![]() 或x = 0 。
或x = 0 。
21.(14分)
[解析]:圆C化成标准方程为:![]()
假设存在以AB为直径的圆M,圆心M的坐标为(a,b)
由于CM⊥L,∴kCM×kL=-1 ∴kCM=![]() ,
,
即a+b+1=0,得b= -a-1 ①
直线L的方程为y-b=x--,即x-y+b-a=0 ∴ CM=![]()
∵以AB为直径的圆M过原点,∴![]()
![]() ,
,![]()
∴![]() ② 把①代入②得
② 把①代入②得 ![]() ,∴
,∴![]()
当![]() 此时直线L的方程为:x-y-4=0;当
此时直线L的方程为:x-y-4=0;当![]() 此时直线L的方程为:x-y+1=0
此时直线L的方程为:x-y+1=0
故这样的直线L是存在的,方程为x-y-4=0 或x-y+1=0.