高二第二学期半期考数学（理科）试卷
（ 满分：150分 时间：120分钟 命题：阙庆洲 ）
一、选择题（本大题共12小题，每小题5分，共60分）
1、设
是异面直线，
也是异面直线，则
的位置关系是
A．异面直线 B．平行直线 C．相交直线 D．位置关系不确定
2、6人站成一排，甲、乙 、丙三人必须站在一起的排列种数为
A．144 B．
3、
A．必要不充分条件 B．充要条件
C．充分不必要条件 D．既不充分又非必要条件
4、已知向量a＝（0，2，1），b＝（－1，1，－2），则a与b的夹角为
A． 0° B． 45° C． 90° D．180°
5、
、
表示直线，
表示平面，下列判断正确的是
A．
，
B．
C．
D．，
6、已知
是三角形
外一点，且
两两垂直，则三角形一定是
A．锐角三角形 B．直角三角形 C．钝角三角形 （D）都有可能
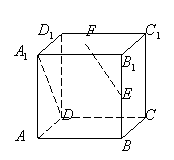
7、如图，在正方体
中，E、F分别是
、
的中点，则直线
与
所成的角为
A．
B．
C．
D．
8、一个棱锥被平行于底面的平面所截，若截面面积与底面面积之比
为1：2，则此棱锥的高被分成的两段之比为
A．
B．1：4 C．
D．
9、短轴长为
，离心率为
的椭圆的两个焦点分别为
、
，过的直线交椭圆于
、
两点，则
的周长为
A．24 B．
10、设地球的半径为
，若甲地位于北纬
东经
，乙地位于南纬
东经，
则甲、乙两地的球面距离为
A．
B．
C．
D．
11、如图，三棱锥O-ABC中，
，则直线OA与平面ABC所成的角是
A. arcsin
B. arccos
C. arcsin
D. arccos
12、直线
与圆
相切，并且在两坐标轴上的截距之和等于
，则直线与两坐标轴围成的三角形的面积等于
A．
B．
C．
或
D．或
二、填空题（本大题共4小题，每小题4分，共16分）
13、由数字1、2、3、4、5组成没有重复数字，且数字1与2不相邻的五位数有_ __个
14、在条件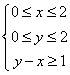
下， 
的最大值是
15、球面上三点、、
，
，若球心到截面的距离等于球半径的一半，则球的体积为
16、如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下4个命题中，假命题是
1等腰四棱锥的腰与底面所成的角都相等
2等腰四棱锥的侧面与底面所成的二面角都相等或互补
3等腰四棱锥的底面四边形必存在外接圆
4等腰四棱锥的各顶点必在同一球面上
三、解答题（第17－21小题每小题12分，第22题14分，6个小题共74分）
17、(本小题满分12分)
解关于
．
18、(本小题满分12分)
一批救灾物资随26辆汽车从某市以x km/h的速度匀速开往
km，问这批物资全部到达灾区，最少要多少小时？
19、(本小题满分12分)
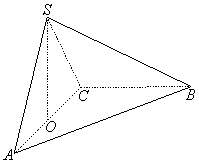
如图，在三棱锥S-ABC中，平面SAC⊥平面ABC，
且△SAC是正三角形, △ABC是等腰直角三角形，其中
AC=CB=2，O是AC的中点．
（1）求证：SO⊥AB；
（2）求二面角B-SA-C的大小．
 |
20、(本小题满分12分)
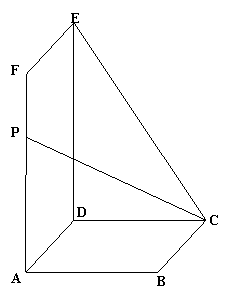
已知：如图，矩形ADEF垂直正方形ABCD，
AF=2AD=2，P为线段AF上一动点。
(Ⅰ)求证：BD⊥CP
(Ⅱ)若AF=3PF，求点P到平面ACE的距离。
(Ⅲ)当P在线段AF上何位置时，P在平面
ECA的射影在∠ACE的平分线上.
21、(本小题满分12分)
经过点
且倾斜角为的直线与圆
的交点是A，B
（1）求弦AB的长度（用的三角函数表示）；
（2）求当弦AB的长度最短时的直线方程.
22、(本小题满分14分)
已知M（－2，0），N（2，0）两点，动点P在y轴上的射影为H，且使
与
分别是公比为2的等比数列的第三、四项.
（1）求动点P的轨迹C的方程；
（2）已知过点N的直线l交曲线C于x轴下方两个不同的点A、B，设R为AB的中点，若过点R与定点Q（0，－2）的直线交x轴于点D（x0，0），求x0的取值范围.