立体几何复习

高　二　数　学（第41周）

主讲教师：刘海滨

主审教师：陈云楼

立体几何复习

　　一、选择题：

　　1、在棱长为a的正方体中，与AD成异面直线，且距离为a的棱共有

A、2条　　　　B、3条　　　　C、4条　　　　 D、5条

　　2、正四棱锥P—ABCD的侧面PAB为等边三角形，E是PC的中点，是异面直线BE与PA所成角的余弦值为

A、　　　　B、　　　　C、　　　　  D、

　　3、有120⁰的二面角—l—，两异面直线a、b，a⊥，b⊥，则ab所成角等于

A、30⁰　　　 B、60⁰　　　　C、45⁰　　　　 D、120⁰

　　4、若正四面体的体积为18cm³，则四面体的棱长为

A、6cm　　　 B、6cm　　　 C、12cm　　　　 D、3cm

　　5、若斜线l与平面所成角为，在内任作l的异面直线a ，则l与a所成的角有

A、最大值，最小值　　　　　　 B、最大值，最小值

C、最大值，最小值　　　　  D、不存在最大值和最小值

　　6、如图，棱长都为2的直平行六面体ABCD—A₁B₁C₁D₁中∠BAD=60⁰，则对角线A₁C与侧面DCC₁D₁所成角的正弦函数值为

A、　　  B、　　  C、　　　 D、

　　7、两个平行于圆锥底面的平面，把圆锥高分成相等三段，那么这个圆锥被分成的三部分的体积比是

A、1 ：2 ：3　　  B、4 ：9 ：27　 C、1 ：7 ：19　　　D、3 ：4 ：5

　　8、平行六面体的棱长都为a，从一个顶点出发的三条棱两两都成60⁰角，则该平行六面体的体积为　　　　　　　　A、a³　　　 B、　　　　C、　　　　 D、

　　9、三棱锥P—ABC的侧棱PA、PB、PC两两垂直，侧面面积分别是6，4，3，则三棱锥的体积是

A、4　　　　  B、6　　　　 C、8　　　　 D、10

　　10、正六棱锥底面周长是6，高是，那么它的侧面积是

A、　　　　 B、6　　　　  C、4　　　　 D、

　　11、正八面体每个面是正三角形，且每一顶点为其一端都有四条棱，则其顶点数V和棱数E值应是

A、V=6，E=12　　B、V=12，E=6　　 C、V=8，E=14　　 D、V=10，E=16

　　二、填空题：

　　1、在北纬45⁰纬度圈上有M、N两点，点M在东经20⁰，点N在西经70⁰，若地球半径为R，则M、N两点的球面距离为　　　　　　 。

　　2、半径为1的球面上有A、B、C三点，已知A和B，A和C之间的球面距离均是，B和C之间的球面距离是，则过A、B、C三点的截面到球心的距离为　　　　　　 。

　　3、一个简单多面体的各个面均为四边形，则它的顶点数V与面数F之间的关系是　　　　　 。

　　4、三个球的半径之比为1 ：2 ：3，则最大球的体积是其他两球体积之和的　　 倍，最大球的表面积是其它两球表面积之和的　　　　　 倍。

　　5、长方体的一条对角线和交于同一个顶点的三个面中的两个面所成的角都为30⁰，则它与另一个面所成的角为　　　　　 。

　　6、长方体的三条棱长a、b、c成等差数列，对角线长为，表面积为22，则体积=　　　　  。

　　7、三棱锥S—ABC中，SA=3，SB=4，SC=4且SA、SA、SC两两垂直，则S到平面ABC的距离为　　　　　  。

　　8、长方体三条棱长分别是AA’=2，AB=3，AD=4，从A点出发，经过长方体的表面到C’的最短距离为　　　　　　  。

　　9、在球心内有相距9cm的两个平行截面，面积分别为49cm²和400cm²，球心不在截面之间，则球的表面积为　　　　　　　 。

　　10、若平行六面体的六个面都是边长为2，且锐角为60⁰的菱形，则它的体积为　　　　　 。

　　三、解答题：

　　1、如图，已知四棱锥V—ABCD的高为h，底面菱形，侧面VDA和侧面VDC所成角为120⁰，且都垂直于底面，另两侧面与底面所成角为45⁰，求棱锥的全面积。

　　2、斜三棱柱A’B’C—ABC中，各棱长都是a，A’B=A’C=a，

　　（1）求证：侧面BCC’B’是矩形；　　（2）求B到侧面ACC’A’的距离。

　　3、如图所示，已知正四棱柱ABCD—A₁B₁C₁D₁的底面边长为3，侧棱长为4，连CD₁作C₁M⊥CD₁交DD₁于M，　 （1）求证：BD₁⊥平面A₁C₁M；　（2）求二面角C₁—A₁M—D₁的大小。

　　4、已知斜三棱柱ABC—A₁B₁C₁D₁中，AC=BC，D为AB的中点，平面ABC⊥平面ABB₁A，异面直线BC₁与AB₁互相垂直。

　　（1）求证：AB₁⊥CD；　　 （2）求证：AB₁⊥平面A₁CD

　　（3）若C₁C与平面ABB₁A­₁距离为1，A₁C=，AB₁=5，求三棱锥A₁—ACD的体积。

　　5、直四棱柱ABCD—A₁B₁C₁D₁中，底面ABCD为梯形AB//CD，且AB=AD=2，∠BAD=60⁰，CD=，AA₁=3， （1）求证：平面B₁BCC₁⊥平面ABC₁D₁ ；（2）求二面角B₁—AD₁—B的大小。

极限、导数复习

　　一、选择题：

　　1、把化成分数是

　　A、　　　　 B、　　　 C、　　  C、

　　2、已知等比数列{a_n}的前三项为a，，，且S_n=a₁+a₂+…a_n，则S_n等于

　　A、　　　　B、6　　　　 C、9　　　　  D、7

　　3、的值等于

　　A、1　　　　B、　　　　 C、　　　　  D、0

　　4、设f(x)=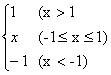 ，则极限的值是

　　A、1　　　 B、—1　　　　C、0　　　　 D、不存在

　　5、f(x)=，则等于

　　A、　　　　 B、0　　　　  C、　　　　  D、不存在

　　6、极限的值为

　　A、　　　　 B、　　　　C、　　　　  D、

　　7、质点M按规律S=2t²+3做直线运动，则质点M在t=2时的瞬时速度是

　　A、12　　　 B、6　　　　 C、4　　　　 D、8

　　8、若函数（—2<x<2），则f(x)有

　　A、极大值为5，极小值为—27　　  B、极大值为5，无极小值

　　C、极大值为5，极小值为—11　　  D、极小值为—27，无极大值

　　9、对于函数f(x)=x³ —3x²，给出命题：

　　（1）f(x)是增函数；　　 （2）f(x)是减函数，无极值；

　　（3）f(x)增区间为（—∞，0），（2，+∞），减区间（0，2）

　　（4）f(0)=0是极大值，f(2)= —4是极小值。

　　其中正确的命题有

　　A、1个　　　　B、2个　　　　 C、3个　　　　 D、4个

　　10、，则q的取值范围

　　A、q<—1　　　 B、q>—1　　　 C、q>0　　　 D、q>

　　二、填空：

　　1、已知f(n)=1+2+…+n （n∈N^*），则的值等于　　　　　 。

　　2、，求a= 　　　　　　 。

　　3、y=2x³在点（1，1）处的切线方程是　　　　　　　　　　　 。

　　4、函数y=x³-2x²+x+1在[-1,2]处的最值。

　　5、用定义的方法，求的导数。

　　6、用总长14.8m的钢条制作一个长方体容器的框架，如果所制作容器的底面一边比另一长0.5m，那么高为多少时容器的容积最大？并求出它的最大容积。

概率、统计复习

　　一、选择题：

　　1、掷两颗骰子，所得点数之和为4的概率是

A、　　 　B、　　　　C、　　　　D、

　　2、停车场可把12辆车停放在一排上，当有8辆车已停放后，而恰有4个空位在一起，这样的事件发生的概率为

A、　　　　B、　　　　 C、　　　　D、

　　3、从长度分别为1，3，5，7，9个单位的5条线段中任取3条作边能组成三角形的概率是

A、　　　　B、　　　　C、　　　　D、

　　4、从标有1，2，3，…，9的9张纸片中任取2张，那么这两张纸片数字之积为偶数的概率是

A、　　　 B、　　　 C、　　　 D、

　　5、20名学生，任意分成甲、乙两组，每组10人，其中2名学生干部恰好被分在不同组内的概率是

A、　　  B、　　  C、　　　 D、

　　6、从装有黑球和白球的口袋内任取2个球（其中黑球和白球都等于2个），那么互斥而不对立的两个事件是

A、至少有1个黑球，至少有1个白球　　 B、恰有一个黑球，恰有2个白球

C、至少有一个黑球，都是黑球　　　　　 D、至少有1个黑球，都是白球

　　7、在5张卡片上分别写上数字1，2，3，4，5，然后把它们混合，再任意排成一行，则得到的数能被5或2整除的概率是

A、0.2　　　 B、0.4　　　 C、0.6　　　　D、0.8

　　8、有3个人，每个人都以相同的概率被分配到4个房间中的一间，则至少有2个人分配到同一房间的概率为

　　A、　　  B、　　  C、　　  D、　

　　9、对一同目标进行三次射击，第一、二、三次射击命中目标的概率分别为0.4，0.5和0.7，则三次射击中恰有一次命中目标的概率是

A、0.36　　　　B、0.64　　　　  C、0.74　　　　  D、0.63

　　10、某机械零件加工由2道工序组成，第1道工序的废品率为a，第2道工序的废品率为b，假定这两道工序出废品是彼此无关的，那么产品的合格率是

A、ab—a—b+1　　 B、1—a—b　　　C、1—ab　　　 D、1—2ab

　　11、有一批蚕豆种子，如果每颗发芽的概率为0.9，播下15粒种子，那么恰有14粒种子发芽的概率是

A、1—0.9¹⁴　　　B、0.9¹⁴　　 C、　　D、

　　二、填空题：

　　12、在100件产品有5件次品，现从中任取3件，（1）都是正品的概率为　　　　，（2）至少有1件次品的概率是　　　　　  ，（3）恰有一件次品的概率是　　　　 。

　　13、用数字1，2，3，4，5组成5位数，其中恰有4个相同数字的概率是　　　 。

　　14、某人有5把钥匙，但忘了开房门的是哪一把，于是他逐个不重复地试开，则

（1）恰好第三次打开房门的概率为　　　　　  ；（2）三次内打开的概率为　　　 。

（3）如果5把内有2把房门钥匙，那么三次内打开的概率是　　　　　  。

　　15、有一道竞赛题，A生解出它的概率为，B生解出它的概率为，C生解出它的概率为，则A、B、C三人独立解答此题只有1人解出的概率为　　　　 ，此题被解出的概率为　　　　　  。

　　16、若以连续两次掷骰子分别得到的点数m、n作为点P的坐标，则点P落在圆x²+y²=16内的概率是　　　　  。

　　17、某班有40名学生，某次测验的均分为75，标准差为5，若数值服从正整分布，问这次测验中低于65分的大约有　　　　个人。

　　三、解答题：

　　18、10张奖券中有2张是有奖的，由甲、乙两人先后各抽一张，求：

　　（1）甲中奖的概率 ；

（2）甲、乙都中奖的概率；

（3）只有乙中奖的概率；

（4）乙中奖的概率。

　　19、要制造一种机器零件，甲机床的废品率是0.04，乙机床的废品率是0.05，从它们制造的产品中，各任意抽取1件，求：

　　（1）其中没有废品的概率 ；

（2）其中至少有一件废品的概率；　

（3）其中都是废品的概率；　　　　 　 

（4）其中恰有一件废品的概率；

（5）其中至多有一件废品的概率。

【参考答案】

立体几何复习

　　一、选择题：

1、C　　　2、B　　　3、B　　　4、A　　　5、A　　　6、D

7、C　　　8、C　　　9、A　　 10、D　　 11、A

二、填空题：

1、　　　　　　　　　　 2、

3、V – F = 2　　　　　　　　 4、3　　 1.8

5、45°　　　　　 　　　　　　6、6

7、　　　　　　　　　  8、

9、　　　　　　　 10、

三、解答题：

1、

2、

3、

4、

5、

极限、导数复习

一、选择题：

1、B　　　2、C　　　3、C　　　4、D　　　5、A

6、B　　　7、D　　　8、B　　　9、B　　 10、D

二、填空：

1、2　　　　　　　　　　　　　 2、1/3

3、3x – 2y – 2 = 0　　　　　　4、y_min = -3 , y_max = 3

5、y′= 2x + x^-2

6、h = 1.2m时，V_max = 1.8m³

概率、统计复习

　　一、选择题：

1、B　　　2、C　　　3、D　　　4、C　　　5、A　　　6、B

7、C　　　8、D　　　9、A　　 10、A　　 11、D

二、填空题：

12、　　 　　 

13、

14、1/5　　 3/5　　

15、　　 3/4

16、2/9

17、1

三、解答题：

18、（1）1/5　　 （2）　　  （3）　　 （4）

19、（1）0.912　　（2）0.088　　 （3）0.002　　 （4）0.086　　 （5）0.998