立体几何练习

立体几何练习

1．在正方体，ABCD－中，E，F，G，H，M，N分别是，BC，AB，，，的中点，求证：这些中点共面．

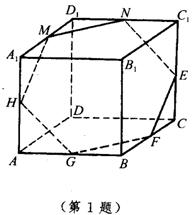
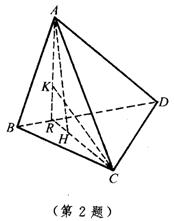
2．在四面体ABCD中，AC⊥BD，AH⊥面BCD，H为垂足，CK⊥面ABD，K为垂足．求证：AH与CK必相交．

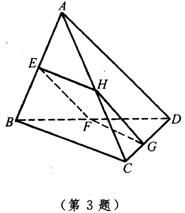
3．ABCD是空间四边形，H，F分别是AC，BD，过H，F且平行于AD的平面分别交AB，CD于E，G．求证：BC∥面EFGH．

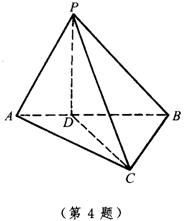
4．AB是Rt△ABC的斜边，P是平面ABC外的一点，且P到△ABC的三个顶点的距离相等．求证：平面PAB⊥平面ABC．

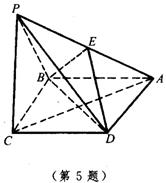
5．已知四棱锥P－ABCD，它的底面ABCD是边长为a的菱形，且∠ABC＝120°，PC⊥面ABCD．又PC＝a，E为PA的中点．

（1）求证：面EBD⊥面ABCD；

（2）求点E到平面PBC的距离；

（3）求二面角A－BE－D的大小．

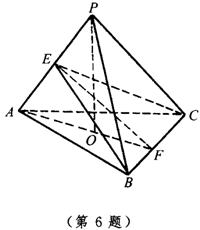
6．正三棱锥P－ABC的高和底面边长都等于a，EF是PA与BC的公垂线，E，F分别为垂足．

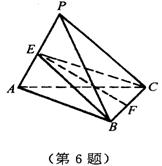
（1）求证：侧棱PA⊥截面BEC；

（2）求截面BEC的面积；

（3）求截面BEC与底面ABC所成二面角的大小．

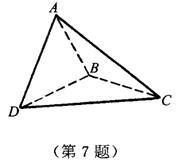
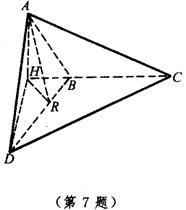
7．如图，△ABC与△BCD所在平面互相垂直，且AB＝BC＝BD，∠ABC＝∠DBC＝120°．求：

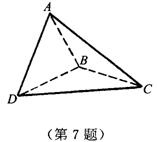
（1）直线AD与面BCD所成的角；

（2）直线AD与BC所成的角；

（3）二面角A－BD－C的大小．

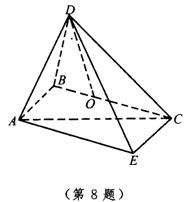
8．如图△ABC是等腰直角三角形，AB＝BC＝4，△BCD是等边三角形，将它们折成直二面角A－BC－D．

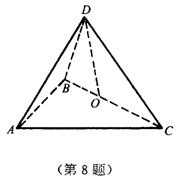
（1）取BC的中点O，证明：DO⊥面ABC；

（2）求二面角D－AB－C的大小；

（3）求AD与平面ABC所成角的正切；

（4）求AD与BC所成角的余弦．

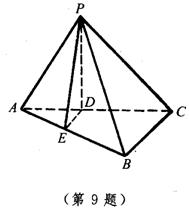
9．如图，在三棱锥P－ABC中，PA＝PC，∠APC＝∠ACB＝90°，∠BAC＝30°，平面PAC⊥平面ABC．

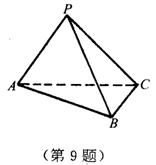
（1）求证：平面PAB⊥平面PBC；

（2）求二面角P－AB－C的大小；

（3）若PA＝2，求三棱锥P－ABC的体积．

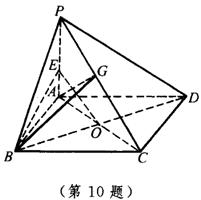
10．如图，在四棱锥P－ABCD中，底面ABCD是平行四边形，PA⊥底面ABCD，且PA＝AD＝2a，AB＝a，AC＝a．

（1）求证：平面PDC⊥平面PAC；

（2）求异面直线PC与BD所成角的余弦值；

（3）设二面角A－PC－B的大小为，求tg．

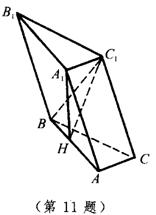
11．如图，斜三棱柱ABC－中， ，AB⊥AC，AB＝3，AC＝2，侧棱与底面成60°角．

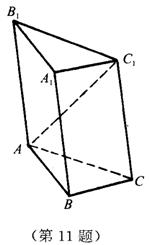
（1）求证：AC⊥面；

（2）求证：在平面ABC上的射影H在直线AB上；

（3）求此三棱柱体积的最小值．

12．设半径为R的地球面上有A，B两地，A地位于东经20°、南纬30°，B地位于东经80°、北纬60°，求A，B两地的球面距离．

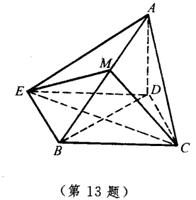
13．如图，在四棱锥A－BCDE中，AD⊥底面BCDE，AC⊥BC，AE⊥BE．

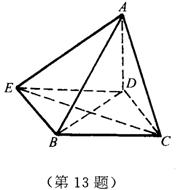
（1）求证：A、B、C、D、E五点都在以AB为直径的同一球面上；

（2）若∠CBE＝90°，CE＝，AD＝1，求B，D两点的球面距离．

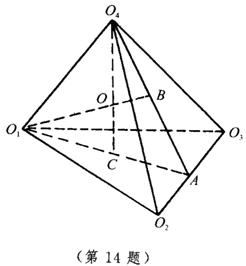
14．有四个半径均为R的球，每个球都和其他三个球相切，求和这四个球都相切的球的半径．

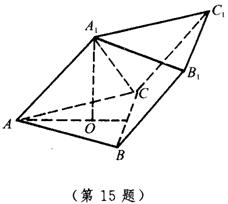
15．如图，斜三棱柱－ABC的底面是边长为2的正三角形，顶点在底面上的射影是△ABC的中心，与AB的夹角是45°．

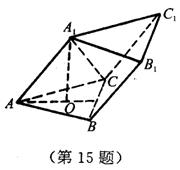
（1）求证：⊥平面；

（2）求此棱柱的侧面积．

16．如图（1），在正方形ABCD的四边，AB，AD，CD，BC上分别取点E，F，G，H，使AE︰EB＝AF︰FD＝CG︰GD＝CH︰HB＝1︰2，把正方形沿BD折起得图（2）．

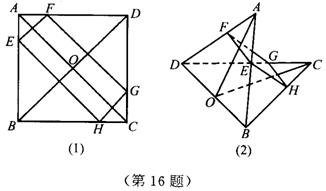
（1）求证：EFGH是矩形；

（2）当二面角A－BD－C是多少时，EFGH为正方形？

（3）当正方形ABCD的边长为3，且EFGH为正方形时，求三棱锥A－BCD的体积．

参考答案

1．连结，MF，∵　NE∥，∥MF，∴　NE∥MF，设NE，MF确定平面为，同理连结NG，EF∥NG．设EF，NG确定平面为，则EF、NE同在平面，内．又EF，NE为两条相交直线，∴　与重合，即M，N，E，F，G共面．同理可证H也在这个平面内．∴　E，F，G，H，M，N六点共面

2．

　　．

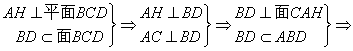
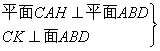
设BD与平面CAH交于R，则AH⊥CR，CK⊥AR．又CK，AH在同一平面内，因此AH与CK必相交

3．∵　AD∥面EFGH，AD平面ACD，而平面EFGH平面ACD＝HG，∴　AD∥HG．在△ACD中，H是AC的中点，故G是CD的中点．同理可证E是AB的中点．于是BC∥FG．又∵是FG平面EFGH，∴　BC∥平面EFGH

4．如图，设D为AB的中点，连结PD，CD，则PD⊥AB．∵　AP＝CP，AD＝CD，∴　△PCD≌△PAD．∴　PD⊥CD．∴　PD⊥面ABC．又PD面PAB，∴　面PAB⊥面ABC

5．（1）连结AC，BD交于F，∴　EF∥PC．∵　PC⊥面ABCD，∴　EF⊥面ABCD，EF面EBD．∴　面EBD⊥面ABCD（2）∵　EF∥PC，∴　EF∥面PBC．∴　E到面PBC的距离是EF到面PBC的距离．∵　面PBC⊥面ABCD，且交线为BC，过F作FH⊥BC于H，则FH⊥面PBC．∴　FH为E到面PBC的距离．∵　∠FCH＝30°，，∴　（3）取BC的中点G，连结FG，AG．∵　面BDE⊥面ABCD，AF⊥BD，∴　AF⊥面BDE．∵　BF＝EF＝，∴　FG⊥BE．∵　，∴　．∴　AG⊥BE．则∠FGA为二面角D－BE－A的平面角．∵　a，．在Rt△GFA中，∴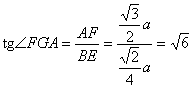　

6．（1）∵　PB＝PC，∠BPE＝∠CPE，PE＝PE，∴　△BPE≌△CPE．∴　BE＝CE．∵　EF⊥BC，∴　F为BC的中点，作PO⊥底面ABC于O．连结AF，则AF⊥BC，且OAF．由三垂线定理得PA⊥BC．又PA⊥EF，∴　PA⊥面EBC（2）在Rt△PAO中，．∵　PA⊥截面EBC，∴　．解得（3）∵　，而BC＝a，∴　．∵　，BC⊥AF，∴　∠AFE就是所求二面角的平面角．在Rt△AEF中，，∴　

7．（1）如图，连结AD，过A在面ABC内作BC的垂线交CB的延长线于H，连结DH，∵　面ACB⊥面BCD，∴　AH⊥面BCD．故∠ADH为AD与面BCD所成的角．由∠ABC＝∠DBC＝120°，AB＝BC＝DB，可得AH＝HD．∴　∠ADH＝45°（2）∵　HD为AD在面BCD上的射影，又BC⊥HD，∴　AD⊥BC．∴　AD与BC成90°角（3）在面BCD内HR⊥BD于R，连结AR．则AR⊥BD，即∠ARH为二面角A－BD－C的平面角的补角．设HB＝a，则．∴　DH＝AH＝．又∠HDB＝30°，∠DHB＝90°，∴ ．又，∴　，．∴　二面角A－BD－C为

8．（1）∵　DO⊥BC，又面BCD⊥面ABC，∴　DO⊥面ABC（2）由已知∠ABC＝90°，AB＝BC＝4，∴　AB⊥BC，又DO⊥面ABC，OB为DB在面ABC内的射影，由三垂线定理知AB⊥BD，则∠DBC为二面角的平面角．∵　∠DBC＝60°，∴　二面角D－AB－C为60°（3）连结AO，则∠DAO为AD与平面ABC所成的角．，，（4）在平面ABC内所AE　 BC，连结CE，则四边形ABCE为正方形．∴　AB＝AE＝BC＝4，DE＝DA＝，

9．（1）∵　面PAC⊥面ABC，BC⊥AC，∴　BC⊥面PAC，BC⊥PA．又PA⊥PC，∴　PA⊥面PBC．∴　PAB⊥面PBC．∴　面PAB⊥PBC（2）作PD⊥AC于D，则PD⊥面ABC，作DE⊥AB于E，连结PE，则∠PED为二面角P－AB－C的平面角，设PA＝PC＝a，则，．在Rt△ABC中，，∴　＝＝（3）∵　PA＝2，则，，．∴　，

10．（1）∵　，∴　AC⊥CD，又PA⊥底面ABCD，∴　PA⊥CD，则CD⊥面PAC．∴　面PAC⊥面PBC（2）连结AC、BD相交于O，则O为AC的中点，取PA的中点E，连结OE，则OE∥PC．∴  ∠BOE为异面直线PC与BD所成的角，．∴ ，，

．由余弦定理得（3）∵　AB⊥面PAC．过A作AG⊥PC于G，连结BG，则∠AGB为所求二面角的平面角，．在Rt△BAG中，

11．（1）∵　∥AC，⊥．∴　AC⊥．又AC⊥AB，∴　AC⊥面（2）由（1）知，AC⊥面，∴　面ABC⊥面．在面内，过作⊥AB于H，则⊥面ABC（3）＝＝．∵　CA⊥AB，∴　CH≥AC＝2．∴　．

12．仿例22，＝

13．（1）取AB的中点M，则ME，MD，MC分别为直角△ABE、直角△ABD、直角△ABC的斜边上的中线，则EM＝BM＝DM＝CM＝AM，即，A，B，C，D，E五点在以AB为直径的球面上（2）∵　AD⊥底面，DC是AC在底面上的射影．而BC⊥AC，∴　BC⊥CD．同理BE⊥ED．又∠EBC＝90°，∴　四边形BCDE为矩形，则BD＝CE＝．又AD＝1，∴　AB＝2，即球半径为1．∴　MB＝MD＝1，由余弦定理，，∴　．∴　B，D两点的球面距离为＝2R＝

14．如图，设这四个球的球心分别是，，，，因每个球都和其他三个球相切，所以为正四面体．设A为的中点，C，B分别是△和△的中心．连结、，其交点为O，则O是与这四个球都相切的球的球心，是与它们都相内切的球的半径．是与它们都相外切的球的半径．

∵　，∴　，．∵　，∴　．∴　所求的球的半径为（）R．

15．（1）∵　△ABC是正三角形，在底面的射影是△ABC的中心，∴　三棱锥是正三棱锥，．在等腰△中，∵　＝45°，∴　∠＝90°，即．同理，∴　面（2）由（1）知．∵　∥，∴　，即四边形是矩形．在△中，．又，∴　．

．．∴　

16．（1）∵　EF∥BD，HG∥BD，且EF＝HG，∴　四边形EFHG为平行四边形．设在图（1）中FG与BD交于M，则EF⊥FG，HG⊥MG，∴　EF⊥MG．∴　EF⊥面FMG．∴　EF⊥FG，即EFGH为矩形（2）若EFGH为正方形，则EF＝FG，在△ABD中，，在图（2）中，，∴　BD＝2AC，又BD＝2BO＝2AO＝2CO，∴ OA＝CO＝AC．∴　∠AOC＝60°，即二面角A－BD－C为60°（3）当正方形ABCD的边长为3时，，当EFHG为正方形时，由于△AOC为正三角形，BD⊥面AOC，连结A与OC的中点，即三棱锥A－BCD的高，可求得高．∴