抛物线的简单几何性质

	学科：数学
	教学内容：抛物线的简单几何性质

【基础知识精讲】

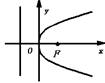
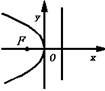
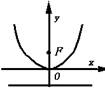
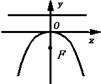
抛物线的几何性质、图形、标准方程列表如下：

图形
标准 方程	y2=2px(p＞0)	y2=-2px(p＞0)	x2=2py(p＞0)	x2=-2py(p＞0)
焦点 坐标	(,0)	(- ,0)	(0, )	(0，-)
准线 方程	x=-	x=	y=-	y=
范围	x≥0	x≤0	y≥0	y≤0
对称轴	x轴	x轴	y轴	y轴
顶点	(0，0)	(0，0)	(0，0)	(0，0)
离心率	e=1	e=1	e=1	e=1
焦半径	｜PF｜=x0+	｜PF｜=-x0	｜PF｜=+y0	｜PF｜=-y0
参数p的几何 意义	参数p表示焦点到准线的距离，p越大，开口越阔.

本节学习要求：

1.抛物线方程的确定，先由几何性质确定抛物线的标准方程，再用待定系数法求其方程.

2.解决有抛物线的弦中点问题及弦长问题与椭圆、双曲线一样，利用弦长公式、韦达定理、中点坐标公式及判别式解决.

3.抛物线中有关轨迹与证明问题也与前面内容一样.常用方法有轨迹法、代入法、定义法.参数法等.证明的方法是解析法.

通过学习本节内容，更进一步培养我们学习数学的兴趣，培养良好的思维品质.运用数形结合的思想方法解决问题，提高分析问题和解决的能力.

【重点难点解析】

1.抛物线的几何性质和椭圆、双曲线比较起来，差别较大，它的离心率等于1；它只有一个焦点、一个顶点、一条对称轴、一条准线；它没有中心.通常称抛物线为无心圆锥曲线，而称椭圆和双曲线为有心圆锥曲线.

应熟练掌握抛物线的四种标准方程.本节重点是抛物线的简单几何性质，难点是几何性质的灵活应用.

例1  已知抛物线顶点在原点，对称轴为x轴，抛物线上的点(x₀，-8)到焦点的距离等于17，求抛物线方程.

分析　设方程为y²=2px(p＞0)或y²=-2px(p＞0)

则　x₀+=17或-x₀=17

即　x₀=17-或x₀=-17

将(17-，-8)代入y²=2px

解得　p=2或p=32

将(-17，-8)代入y²=-2px

解得　p=2或p=32

∴所求抛物线方程为y²=±4x或y²=±64x.

例2  求抛物线y²=4x中斜率为2的平行弦中点的轨迹方程.

分析　本例可设平行弦的纵截距为参数、运用判别式及韦达定理、中点坐标公式来求，也可设点参数运用点差法求解.

设AB是抛物线中斜率为2的平行弦中任一条弦，A(x₁，y₁)，B(x₂，y₂)AB中点M(x,y)

由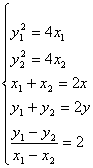

得：y=1

代入y²=4x

得x=

∴轨迹方程为y=1(x＞)

例3  设点A和B为抛物线y²=4px(p＞0)上原点以外的两个动点.已知OA⊥OB，OM⊥AB于M，求点M的轨迹方程，并说明表示什么曲线.

分析　设A(4pt²₁,4pt₁)，B(4pt²₂,4pt₂)，OA、OB的斜率分别为k_OA、k_OB

则　k_OA=,k_OB=

由OA⊥OB，得

k_OA·k_OB==-1t₁t₂=-1　　　　　　　　　　　　　　 ①

∵点A在AB上，得直线AB的方程为

y-4pt₁= (x-4pt²₁)　　　　　　　　　　　　　　　②

由OM⊥AB，得直线OM方程为

y=-(t₁+t₂)x　　　　　　　　　　　　　　　　　　　　　③

设点M(x,y),则x,y满足②③两式

将②化为：y(t₁+t₂)=x+4pt₁t₂=x-4p　　　　　　　　　　　④

由③×④得：x²+y²-4px=0

∵A、B是原点以外的两点

∴x≠0

∴点M的轨迹是以(2p,0)为圆心，以2p为半径的圆(去掉原点).

【难题巧解点拨】

例1  已知抛物线y²=2px上两点A、B，BC⊥x轴交抛物线于C，AC交x轴于E，BA延长交x轴于D，求证：O为DE中点.

分析　只需证出D、E两点的横坐标互为相反数即可，设A(2pt²₁,2pt₁)，B(2pt₂²,2pt₂)则

C(2pt²₂,-2pt₂)

AC：y-2pt₁=(x-2pt²₁)

令y=0,得x_D=2pt₁t₂

BA：y-2pt₁= (x-2pt²₁)

令y=0,得x_E=-2pt₁t₂

∴x_D+x_E=0

即O为DE中点.

例2　设抛物线过定点A(0，2)且以x轴为准线.

(Ⅰ)试求抛物线顶点M的轨迹C的方程；

(Ⅱ)如果点P(a,1)不在线段y=1(-2≤x≤2)上，那么当a取何值时，过P点存在一对互相垂直的直线同时与曲线C各有两个交点?

分析　(Ⅰ)设抛物线顶点M(x,y)，y＞0，则其焦点为F(x,2y).

据抛物线定义有

=2

即　+(y-1)²=1(y≠0)

∴抛物线顶点M的轨迹C的方程是

+(y-1)²=1(y≠0)

(Ⅱ)过P点的直线可设为l:y-1=k(x-a).由已知P(a,1)不在曲线C上，则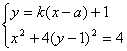

消去y，得x²+4k²(x-a)²=4

即(1+4k²)x²-8k²ax+4(k²a²-1)=0

∴△=16［k²(4-a²)+1］

过点P存在一对互相垂直的直线同时与曲线C各有两个不同的交点的充要条件是关于斜率k的不等式组

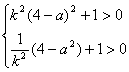有解

∵点P不在直线y=1(-2≤x≤2)上，∴｜a｜＞2，4-a²＜0.

∴上不等式组可化为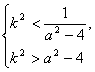

∴a²-4<解a²＜5

又｜a｜＞2,∴2＜｜a｜＜　即a∈(-,-2)∪(2, )

【命题趋势分析】

本节与椭圆、双曲线的相同内容相似，都是高考的重要内容.圆锥曲线的基础知识；直线与圆锥曲线的位置关系、弦长、中点弦及弦的中点的轨迹问题；圆锥曲线中的有关最值问题等等.本章内容为高考压轴题的高频题.

【典型热点考题】

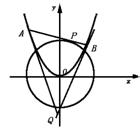
例1  抛物线y=x²的弦AB保持与圆x²+y²=1相切移动，求过A、B的抛物线的切线交点的轨迹方程.

分析一　如图，设抛物线弦AB与圆x²+y²=1相切于P(x₀,y₀),则过P点的圆的切线方程为x₀x+y₀y=1.

由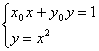得y₀x²+x₀x-1=0

设A的坐标为(x₁,x²₁),B(x₂,x²₂)，由韦达定理，得

x₁+x₂=-,x₁·x₂=-

又过A、B两点的抛物线的切线方程分别为

y+x₁²=2x₁x,y+x²₂=2x₂x，

则两切线交点Q(x,y)是方程组

　　　　　　 

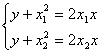
①-②得x²₁-x²₂=2(x₁-x₂)x.

∴　2x=x₁+x₂=- 　　　　　　　 ③

①×x₂-②×x₁得(x₂-x₁)y+x₁x₂(x₁-x₂)=0

∴y=x₁x₂=-　　　　　　　　　  ④

由③、④得x₀=,y₀=-　∵P(x₀,y₀)在圆x²+y²=1上，

∴()²+(-)²=1

即　y²-4x²=1,这是双曲线.

由条件知，所求轨迹是焦点在y轴上，a=1、b=的双曲线的下支的一部分.

分析二  设抛物线的弦AB与圆切于点P(x₀,y₀)，则过P点的圆的切线AB的方程为

　　　　　  x₀x+y₀y=1　　　　　　　　　　　　　 ①

设过A、B两点的抛物线切线交点为Q(α，β)则AB为抛物线的切点弦，其方程为

　　　　　  y+β=2αx　　　　　　　　　　　　  ②

由①、②表示同一直线，于是有

==

∴x₀=　y₀=-

∵P(x₀,y₀)在圆x²+y²=1上，∴()²+(-)²=1,

即β²-4α²=1,故  y²-4x²=1(x∈R,y＜0)

例2  某蔬菜基地种植西红柿，由历年市场行情得知，从2月1日起的300天内，西红柿市场售价与上市时间的关系用如图甲所示的一条折线表示；西红柿的种植成本与上市时间的关系用如图乙所示的抛物线段表示.

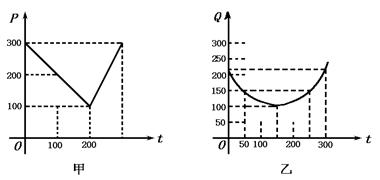
(1)写出如图甲所示市场售价与时间的函数关系式P＝f(t)；写出如图乙所示种植成本与时间的函数关系式Q＝g(t).

(2)认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大?

(注：市场售价和种植成本的单位：元/10²kg，时间单位：天)

解：(1)f(t)＝

g(t)＝ (t-150)²+100,0≤t≤300.

(2)设t时刻的纯收益为h(t)，则由题意得

h(t)＝f(t)-g(t),

即h(t)＝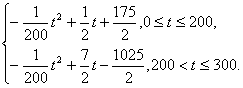

当0≤t≤200时，配方整理得

h(t)＝-(t-50)²+100,

所以，当t＝50时，h(t)取得区间［0，200］上的最大值100；

当200<t≤300时，配方整理得

h(t)＝-(t-350)²+100

所以，当t＝300时，h(t)取得区间(200，300］上的最大值87.5.

综上，由100>87.5可知，h(t)在区间［0，300］上可以取得最大值100，此时t＝50，即从2月1日开始的第50天时，上市的西红柿纯收益最大.

【同步达纲练习】

A级

一、选择题

1.若A是定直线l外的一定点，则过A且与l相切圆的圆心轨迹是(　　)

A.圆　　　　　　B.椭圆　　　　　C.双曲线一支　　　　D.抛物线

2.抛物线y²=10x的焦点到准线的距离是(　　)

A.2.5　　　　　 B.5　　　　　　 C.7.5　　　　　　　 D.10

3.已知原点为顶点，x轴为对称轴的抛物线的焦点在直线2x-4y+11=0上，则此抛物线的方程是(　　)

A.y²=11x　　　　B.y²=-11x　　　 C.y²=22x　　　　　　D.y²=-22x

4.过抛物线y²=2px(p＞0)的焦点且垂直于x轴的弦AB，O为抛物线顶点，则∠AOB(　　)

A.小于90°　　　　　　　　　　　B.等于90°

C.大于90°　　　　　　　　　　　D.不能确定

5.以抛物线y²=2px(p＞0)的焦半径｜PF｜为直径的圆与y轴位置关系为(　　)

A.相交　　　　　B.相离　　　　　C.相切　　　　　　　D.不确定

二、填空题

6.圆心在抛物线y²=2x上，且与x轴和该抛物线的准线都相切的圆的方程是　　　　　　　 .

7.若以曲线+=1的中心为顶点，左准线为准线的抛物线与已知曲线右准线交于A、B两点，则｜AB｜=　　　　　　　 .

8.若顶点在原点，焦点在x轴上的抛物线截直线y=2x+1所得的弦长为，则此抛物线的方程是　　　　　　　 .

三、解答题

9.抛物线x²=4y的焦点为F，过点(0，-1)作直线l交抛物线A、B两点，再以AF、BF为邻边作平行四边形FABR，试求动点R的轨迹方程.

10.是否存在正方形ABCD，它的对角线AC在直线x+y-2=0上，顶点B、D在抛物线y²=4x上?若存在，试求出正方形的边长；若不存在，试说明理由.

AA级

一、选择题

1.经过抛物线y²=2px(p＞0)的所有焦点弦中，弦长的最小值为(　　)

A.p　　　　 　　B.2p　　　　　　C.4p　　　　　　D.不确定

2.直线y=kx-2交抛物线y²=8x于A、B两点，若AB的中点横坐标为2，则｜AB｜为(　　)

A.　　　　　B.4　　　　 C.2　　　　 D.

3.曲线2x²-5xy+2y²=1(　　)

A.关于x轴对称　　　　　　　

B.关于y轴对称

C.关于原点对称，但不关于y=x对称

D.关于直线y=x对称也关于直线y=-x对称

4.若抛物线y²=2px(p＞0)的弦PQ的中点为(x₀,y₀)(y≠0)，则弦PQ的斜率为(　　)

A.-　　　　　B.　　　　　 C.px_-　　　　　 D.-px₀

5.已知抛物线y²=2px(p＞0)的焦点弦AB的两端点坐标分别为A(x₁,y₁)，B(x₂,y₂)，则的值一定等于(　　)

A.4　　　　　　 B.-4　　　　　　　　C.p²　　　　　　D.-p²

二、填空题

6.抛物线y²=4x的弦AB垂直于x轴，若AB的长为4，则焦点到AB的距离为　　　　　　　 .

7.以椭圆+y²=1的右焦点F为焦点，以原点为顶点作抛物线，抛物线与椭圆的一个公共点是A，则｜AF｜=　　　　　　　 .

8.若△OAB为正三角形，O为坐标原点，A、B两点在抛物线y²=2px上，则△OAB的周长为　　　　　　　 .

三、解答题

9.抛物线y=-与过点M(0，-1)的直线l相交于A、B两点，O为坐标原点，若直线OA和OB斜率之和为1，求直线l的方程.

10.已知半圆的直径为2r，AB为直径，半圆外的直线l与BA的延长线垂直，垂足为T，且｜TA｜=2a(2a＜),半圆上有M、N两点，它们与直线l的距离｜MP｜、｜NQ｜满足条件｜MP｜=｜AM｜,｜NQ｜=｜AN｜，求证：｜AM｜+｜AN｜=｜AB｜.

【素质优化训练】

一、选择题

1.过点A(0，1)且与抛物线y²=4x有唯一公共点的直线的条数为(　　)

A.1　　  　　　 B.2　　　　　　 C.3　　　　　　 D.4

2.设抛物线y=ax²(a＞0)与直线y=kx+b相交于两点，它们的横坐标为x₁,x₂,而x₃是直线与x轴交点的横坐标，那么x₁、x₂、x₃的关系是(　　)

A.x₃=x₁+x₂　　　 B.x₃=+　　　　C.x₁x₂=x₂x₃+x₃x₁　 D.x₁x₃=x₂x₃+x₁x₂

3.当0＜k＜时，关于x的方程=kx的实根的个数是(　　)

A.0个　　　　　 B.1个　　  　　 C.2个　　  　　 D.3个

4.已知点A(1，2)，过点(5，-2)的直线与抛物线y²=4x交于另外两点B、C，则△ABC是(　　)

A.锐角三角形　　　　  　　　　　B.钝角三角形

C.直角三角形　　　　 　　　　　 D.不确定

5.将直线x-2y+b=0左移1个单位，再下移2个单位后，它与抛物线y²=4x仅有一个公共点，则实数b的值等于(　　)

A.-1　　  　　　B.1　　　　　　 C.7　　　　　　 D.9

二、填空题

6.抛物线y²=-8x被点P(-1，1)所平分的弦所在直线方程为　　　　　　　 .

7.已知抛物线y²=2x的弦过定点(-2，0)，则弦AB中点的轨迹方程是　　　　　　　 .

8.已知过抛物线y²=2px的焦点F的弦AB被F分成长度为m、n的两部分，则+=　　　　　　　 .

三、解答题

9.已知圆C过定点A(0，p)(p＞0)，圆心C在抛物线x²=2py上运动，若MN为圆C在x轴上截得的弦，设｜AM｜=m,｜AN｜=n，∠MAN=θ.(1)当点C运动时，｜MN｜是否变化?写出并证明你的结论?(2)求+的最大值，并求取得最大值时θ的值和此时圆C的方程.

10.已知抛物线y²=4ax(0＜a＜1)的焦点为F，以A(a+4,0)为圆心，｜AF｜为半径在x轴上方作半圆交抛物线于不同的两点M和N，设P为线段MN的中点，

(Ⅰ)求｜MF｜+｜NF｜的值；

(Ⅱ)是否存在这样的a值，使｜MF｜、｜PF｜、｜NF｜成等差数列?如存在，求出a的值，若不存在，说明理由.

【生活实际运用】

1.已知点P(x₀,y₀)在抛物线含焦点的区域内，求证以点P为中点的抛物线y²=2px(p＞0)的中点弦方程为

yy₀-p(x+x₀)=y²₀-2px₀

注：运用求中点弦的方法不难求出结论，这一结论和过抛物线y²=2px上点的切线方程有什么联系?

若P(x₀,y₀)为非对称中心，将抛物线y²=2px换成椭圆+=1或双曲线-=1，它们的中点弦存在的话，中点弦方程又将如何?证明你的结论.

中点弦方程在高考中多以选择题、填空题的形式出现.

2.公园要建造一个圆形的喷水池，在水池中央垂直于水面安装一个柱子OA，O恰在圆形水面中心，OA=1.25米.安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路经落下，且在过OA的任一平面上抛物线路径如图所示，为使水流形状较为漂亮，设计成水流在到OA距离1米处达到距水面最大高度2.25米.如果不计其它因素，那么水池的半径至少要多少米，才能使喷出的水流不致落到池外?

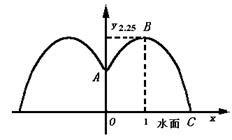
分析　根据图形的对称性，设出并求出一边的抛物线的方程，便可求出水池的半径.

以OA所在直线为y轴，过O点作oy轴的垂直线ox轴，建立直角坐标系如图

依题意A(0，1.25)，设右侧抛物线顶点为则B(1，2.25)，抛物线与x轴正向交点为C，OC即圆型水池的半径.

设抛物线ABC的方程为

(x-1)²=-2p(y-2.25)

将A(0，1.25)代入求得p=

∴抛物线方程为(x-1)²=-(y-2.25)

令y=0，(x-1)²=1.5²,x=2.5(米)

即水池的半径至少要2.5米，才能使喷出的水流不致落到池外.

【知识验证实验】

1.求函数y=-的最大值.

解：将函数变形为y=-，由几何意义知，y可以看成在抛物线f(x)=x²上的点P(x,x²)到两定点A(3，2)和B(0，1)的距离之差，∵｜PA｜-｜PB｜≤｜AB｜，∴当P、A、B三点共线，且P在B的左方时取等号，此时P点为AB与抛物线的交点，即P为(，)时，y_max=｜AB｜=.

2.参与设计小花园的喷水池活动.

要求水流形状美观，水流不落池外.

【知识探究学习】

1.如图，设F是抛物线的焦点，M是抛物线上任意一点，MT是抛物线在M的切线，MN是法线，ME是平行于抛物线的轴的直线.求证：法线MN必平分∠FME，即φ₁=φ₂.

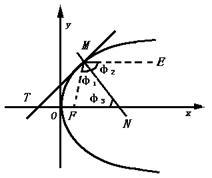
解：取坐标系如图，这时抛物线方程为y²=2px.(p＞0)，因为ME平行x轴(抛物线的轴)，∴φ₁=φ₂,只要证明φ₁=φ₃，也就是△FMN的两边FM和FN相等.设点M的坐标为(x₀,y₀)，则法线MN的方程是y-y₀=-(x-x₀),令y=0，便得到法线与x轴的交点N的坐标(x₀+p,0)，所以｜FN｜=｜x₀+p-｜=x₀+,又由抛物线的定义可知，｜MF｜=x₀+,∴｜FN｜=｜FM｜,由此得到φ₁=φ₂=φ₃，若M与顶点O重合，则法线为x轴，结论仍然成立.

2.课本第124页阅读材料：

圆锥曲线的光学性质及其应用

参考答案:

【同步达纲练习】

A级

1.D　2.B　3.D  4.C　5.C　6.(x-)²+(y±1)²=1　7.　8.y²=12x或y²=-4x

9.解：设R(x,y),∵F(0,1),∴平行四边形FARB的中心为C(,),l:y=kx-1,代入抛物线方程，得x²-4kx+4=0,设A(x₁,y₁),B(x₂,y₂),则x₁+x₂=4k,x₁x₂=4，且△=16k²-16＞0，即k＞1　　①，

∴y₁+y₂===4k²-2,∵C为AB的中点.∴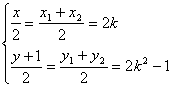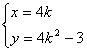消去k得x²=4(y+3),由①得，｜x｜＞4，故动点R的轨迹方程为x²=4(y+3)(｜x｜＞4).

10.解：设存在满足题意的正方形.则BD：y=x+b,代入抛物线方程得x²+(2b-4)x+b²=0,∴△=(2b-4)²-4b²=16-16b＞0,∴b＜1,　　①，设B(x₁,y₁),D(x₂,y₂),BD中点M(x₀,y₀),则x₁+x₂=4-2b,∴x₀=2-b,y₀=x₀+b=2,∵M在AC直线上，∴(2-b)+2-2=0，∴b=2与①相矛盾，故不存在满足要求的正方形.

AA级

1.B　2.C　3.D  4.B　5.B　6.2  7.9-18　8.12p

9.解：设l:y=kx-1,代入y=-,得x²+2kx-2=0，设A(x₁,y₁),B(x₂,y₂)，则x₁+x₂=-2k,x₁x₂=-2,又+=+=2k-=2k-=k=1，∴直线l的方程为y=x-1.

10.证明：由｜MP｜=｜AM｜,｜NQ｜=｜AN｜知M、N在以l准，A为焦点的抛物线上，建立直角坐标系，设抛物线方程为y²=2px，又｜TA｜=2a=p,∴抛物线方程为y²=4ax，又圆的方程为(x-a-r)²+y²=r²，将两方程相减可得：x²+2(a-r)x+a²+2ar=0，设M(x₁,y₁),N(x₂,y₂)，则x₁+x₂=2r-2a,∴｜AM｜+｜AN｜=｜PM｜+｜QN｜=x₁+x₂+2a=2r,即｜AM｜+｜AN｜=｜AB｜

【素质优化训练】

1.C　2.C　3.D  4.C　5.C　6.4x+y+3=0　7.y²=x+2(在已知抛物线内部的部分)　8.

9.解：(1)设圆心C(x₀,y₀),则x²₀=2py₀，圆C的半径｜CA｜=，其方程为(x-x₀)²+(y-y₀)²=x²₀+(y₀-p)²,令y=0，并将x²₀=2py₀，代入，得x²-2x₀x+x²₀-p²=0，解得x_m=x₀-p,x_N=x₀+p,∴｜MN｜=｜x_N-x_M｜=2p(定值)

(2)∵m=｜AM｜=,n=｜AN｜=,∴m²+n²=4p²+2x²₀,m·n=，∴+====

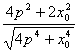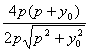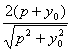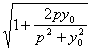=2≤2，当且仅当y₀=p时等号成立，x₀=±p，此时△MCN为等腰直角三角形，且∠MCN=90°，∴∠MAN=∠MCN=45°，故当θ=45°时，圆的方程为(x- p)²+(y-p)²=2p²或(x+p)²+(y-p)²=2p²

10.解：(1)由已知得F(a,0),半圆为［x-(a+4)］²+y²=16(y≥0)，设M(x₁,y₁),N(x₂,y₂)，则｜MF｜+｜NF｜=x₁+x₂+2a=2(4-a)+2a=8

(2)若｜MF｜、｜PF｜、｜NF｜成等成数列，则有2｜PF｜=｜MF｜+｜NF｜,另一方面，设M、P、N在抛物线的准线上的射影为M′、P′、N′，则在直角梯形M′MNN′中，P′P是中位线，又有2｜P′P｜=｜M′M｜+｜N′N｜=｜MF｜+｜FN｜,因而｜PF｜=｜P′P｜,∴P点应在抛物线上，但P点是线段MN的中点，即P并不在抛物线上，故不存在使｜MF｜、｜PF｜、｜NF｜成等差数列的a值.