双曲线其标准方程-高中二年级数学试题练习、期中期末试卷、测验题、复习资料-高中数学试卷-试卷下载

学科：数学

教学内容：双曲线及其标准方程

【基础知识精讲】

1.双曲线的定义

平面内与两定点F₁、F₂的距离差的绝对值是常数(大于零小于｜F₁F₂｜)的点的轨迹叫双曲线.两定点F₁、F₂是焦点，两焦点间的距离｜F₁F₂｜是焦距，用2c表示.常数用2a表示.

(1)若｜MF₁｜-｜MF₂｜=2a时，曲线只表示焦点F₂所对应的一支双曲线.

(2)若｜MF₁｜-｜MF₂｜=-2a时，曲线只表示焦点F₁所对应的一支双曲线.

(3)若2a=2c时，动点的轨迹不再是双曲线，而是以F₁、F₂为端点向外的两条射线.

(4)若2a＞2c时，动点的轨迹不存在.

2.双曲线的标准方程

-=1(a＞0,b＞0)焦点在x轴上的双曲线；

-=1(a＞0,b＞0)焦点在y轴上的双曲线.

判定焦点在哪条坐标轴上，不像椭圆似的比较x²、y²的分母的大小，而是x²、y²的系数的符号，焦点在系数正的那条轴上.

本节学习方法：

本节主要数学思想和方法：方程思想，利用双曲线的定义等条件求双曲线方程.常用特定系数法、定义法和轨迹法等.

双曲线和椭圆一样，都是解析几何的重要部分，双曲线的学习可通过与椭圆对比去掌握.它与直线、圆联系密切，涉及到距离公式、弦长问题，面积公式及方程中的韦达定理等知识，也是高考的重点内容.

【重点难点解析】

1.双曲线的定义，标准方程与椭圆类似，本小节在数学思想和方法上没有新内容，学习中应着重对比椭圆与双曲线的相同点和不同点，特别是它们的不同点.

2.与建立椭圆的标准方程一样，建立双曲线的标准方程是，从“平面内到两定点的距离差的绝对值是常数(与椭圆不同，这个常数要大于0且小于｜F₁F₂｜)的点M的轨迹”这个双曲线的定义出发，推导出它的标准方程.推导过程说明，双曲线上任意一点的坐标都适合方程-=1；但关于坐标适合方程-=1的点都在双曲线上，即完备性未加以证明.

例1　若方程+=1表示双曲线，则实数m的取值范围是(　　)

A.-3＜m＜2或m＞3　　　　　　 B.m＜-3或m＞3

C.-2＜m＜3　　　　　　　　　　　D.-3＜m＜3或m＞3

分析　该方程表示双曲线，则x²与y²项的系数的符号相反，即(2-m)(｜m｜-3)＜0，将问题转化为不等式的求解.

答：A

例2　求与椭圆+=1共焦点，且过点(3，)的双曲线的方程.

分析一　由题意知所求双曲线的焦点在x轴上，且焦距为8，∴c=4,设所求双曲线方程为-=1代入点(3，)，得λ²=7，故所求双曲线方程为-=1.

分析二　运用与椭圆共焦点的曲线系方程.设所求双曲线方程为+=1，代入点(3，)，得λ=16或λ=-7(舍)，故所求双曲线方程为-=1.

例3　课本第108页习题8.3第一题：△ABC一边的两个端点是B(0，6)和C(0，-6)，另两边所在直线的斜率之积是，求顶点A的轨迹.

分析　其顶点A的轨迹方程求得：-=1(x≠0).若将问题一般化：B(0，a)、C(0，-a) k_AB·k_AC=，则顶点A的轨迹方程为：-=1(x≠0).若B(bcotφ，acosφ)、C(-cotφ，-acscφ).k_AB·k_AC=，则顶点A的轨迹会是怎样?

反之，双曲线-=1(x≠0)上任一点到B(0，a)，C(0，-a)两点的连线的斜率之和，等于;若改变B、C的位置保持B、C两点关于原点对称于双曲线上，k_AB·k_AC=是否成立.

总之，同学们在学习过程中要多动手、多思考，举一反三，做到“以点代面，以少胜多”.

【难题巧解点拨】

例1　一动圆与圆(x+3)²+y²＝1外切又与圆(x-3)²+y²＝9内切，求动圆圆心轨迹方程.

分析　如图，设动圆M与⊙O₁外切于A，与⊙O₂内切于B，由位置关系可得数量关系：

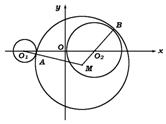
｜MO₁｜＝｜MA｜+1 ｜MO₂｜＝｜MB｜-3

由｜MA｜＝｜MB｜可得｜MO₁｜-｜MO₂｜＝4

由定义可知M点轨迹为双曲线的一支.

解：如图，设动圆圆心M坐标为M(x,y)，圆M与圆O₁外切于A，与圆O₂内切于B，则，MO₁＝｜MA｜+1①，｜MO₂｜＝｜MB｜-3②，①-②：｜MO₁｜-｜MO₂｜＝4

由双曲线定义知，M点轨迹是以O₁(-3，0)O₂(3，0)为焦点2a＝4的双曲线的右支

∴b²＝3²-2²＝5

∴所求轨迹方程为：-＝1(x≥2)

说明：在求轨迹方程时，要注意使用曲线的定义，此时的思路：位置关系(内切，外切)数量关系(｜MO₁｜＝r+r₁,｜MO₂｜＝r-r₂其中r为动圆半径)曲线形状(写出标准方程)，可以简化运算.同时应注意定义中是到两定点距离的绝对值，此时不含绝对值，要求｜MO₁｜>｜MO₂｜，所以是双曲线的右支，而不是整个双曲线.

例2　过双曲线-＝1的右焦点作倾角为45°的弦，求弦AB的中点C到右焦点F的距离，并求弦AB的长.

分析　将直线方程与双曲线方程联立，求出A、B两点的坐标，再求其中点，由两点的距离公式求出｜CF｜.

解：∵双曲线的右焦点为F(5，0)，直线AB的方程为y＝x-5，故

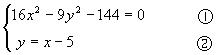
消去y，并整理得

7x²+90x-369＝0　　　　　　　　　③

此方程的两个根x₁、x₂是A、B两点的横坐标，设AB的中心点C的坐标为(x,y)，则

x＝＝＝-.

C点的坐标满足方程②，故

y＝--5＝-

∴｜CF｜＝＝(5+)

＝

又设A点坐标为(x₁,y₁),B点坐标为(x₂,y₂)，则y₁＝x₁-5,y₂＝x₂-5.

∴y₁-y₂＝x₁-x₂，

｜AB｜＝

＝

由方程③知

x₁+x₂＝-,x₁·x₂＝-

∴｜AB｜＝

＝＝＝27

点评：利用韦达定理及两点间距离公式求弦长.

【命题趋势分析】

双曲线与直线、圆和椭圆联系密切，涉及到距离公式、弦长及面积公式、方程中的韦达定理和判别式的运用；还涉及到弦的中点轨迹问题、中点弦问题，对称问题与最值问题等都是高考的重要内容.如“能力演练”中有许多曾是高考题或样题，同学们在学习中应该重基础知识和基本的数学思想数学方法的运用.训练能力，创新思维，做到举一反三.触类旁通.

【典型热点考题】

例1　设F₁和F₂为曲线-y²=1的两个焦点，点P在双曲线上且满足∠F₁PF₂=90°，则求△F₁PF₂的面积.

分析一　依题意求出P点的纵坐标，据面积公式计算△F₁PF₂的面积.

设P(x₁,y₁),由PF₁⊥PF₂得

·=-1

即　y²₁=5-x²₁

又　x²₁-4y²₁=4

联立解得y₁=±

∴=｜F₁F₂｜·｜y₁｜=·2c· =1

分析二　运用双曲线定义解题

由点P在双曲线上，知

｜｜PF₁｜-｜PF₂｜｜=4且｜PF₁｜²+｜PF₂｜²=20

联立解得｜PF₁｜·｜PF₂｜=2

∴=｜PF₁｜·｜PF₂｜=1

例2　已知l₁、l₂是过点P(-，0)的两条互相垂直的直线，且l₁、l₂与双曲线y²-x²=1各有两个交点，分别为A₁、B₁和A₂、B₂.

(1)求l₁的斜率k₁的取值范围.

(2)若｜A₁B₁｜=｜A₂B₂｜；求l₁、l₂的方程.

分析　设直线斜率为k，联立方程组求解.

(1)因为若l₁、l₂中有一条斜率不存在，就可推出另一条斜率为零而与双曲线不相交，所以l₁、l₂的斜率k₁、k₂均不为零.

设l₁:y=k₁(x+),

　l₂:y=-(x+)

把它们代入双曲线方程分别得

(k²₁-1)x²+2k²₁x+2k²₁-1=0　　　　　　　　　　　 ①

(k²₁-1)x²-2x+k²₁-2=0　　　　　　　　　　　 ②

当k₁=±1时，方程①、②均为一次方程不符合题意，

所以，当k₁≠±1时由①、②的判别式都大于零得

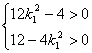
k₁∈(-，-)∪(，)且k₁≠±1

(2)由①、②可知

｜A₁B₁｜ =·

=·

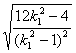
｜A₂B₂｜=·

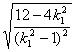
∵｜A₁B₁｜=｜A₂B₂｜

∴解得　k₁=±,k₂=±

∴所求直线方程为

l₁:y=(x+),l₂:y=- (x+)

或l₁:y=- (x+),l₂:y=(x+).

例3　如图，给出定点A(a,0)，(a＞0)和直线l:x=-1.B是直线l上的动点，∠BOA的角平分线交AB于C.求点C的轨迹方程，并讨论方程表示的曲线类型与a值的关系.

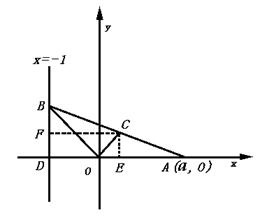
分析　设B(-1，y₀)，C(x,y)，由角平分线的性质有

=,当y₀≠0时，又由平行线性质有

===

∴==

即有==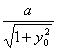

(易知y与y₀-y同号，0＜x＜a)

由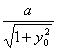=得

a²(x+1)²=(a-x)²(1+y²₀)　　　　　　　　　　　　①

又由=得y₀=·y　　　　 ②

由①、②消去y₀并整理得

(1-a)x²-2ax+(1+a)y²=0　　　　　　　　　　　　③

当y₀=0时易知点C即为原点，此时x=0，y=0，亦满足③，故所求点C的轨迹方程是：

(1+a)x²-2ax+(1+a)y²=0(0≤x＜a)④

(1)当a=1时，方程为y²=x(0≤x＜1)

表示抛物线弧段.

(2)当a≠1时，④变形为

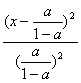+＝1(0≤x＜a)

当0＜a＜1时，方程④表示椭圆弧段；

当a＞1时，方程④表示双曲线一支的弧段.

【同步达纲检测】

A级

一、选择题

1.设θ∈(，π)则方程x²·cosθ-y²secθ=1所表示的曲线是(　　)

A.焦点在x轴上的双曲线　　　　　B.焦点在y轴上的椭圆

C.焦点在x轴上的椭圆　　　　　　　　D.焦点在y轴上的双曲线

2.如果双曲线-y²=1的两个焦点为F₁、F₂，A是双曲线上一点，且｜AF₁｜=5，那么｜AF₂｜等于(　　)

A.5+　　 B.5+2　　 C.8　　　　 D.11

3.与两圆x²+y²=1和x²+y²-8x+7=0都相切的圆的圆心轨迹是(　　)

A.两个椭圆　　　　　　　　　　　B.两条双曲线

C.一条双曲线和一条直线　　　　　D.一个椭圆与一条双曲线

4.以椭圆+=1的焦点为顶点，以这个椭圆的长轴的端点为焦点的双曲线的方程是(　　)

A.-y²=1　　　　　　　　　　　　B.y²- =1

C.-=1　　　　　　　　　　　　D. -=1

5.设动点P到定点F₁(-5，0)的距离与它到定点F₂(5，0)的距离的差等于6，则P点轨迹方程是(　　)

A. -=1　　　　　　　　　 B. -=1

C. -=1(x≥3)　　　　　　 D. -=1(x≤-3)

二、填空题

6.若椭圆mx²+ny²=1(0＜m＜n)和双曲线ax²-by²=1(a＞0,b＞0)有相同的焦点F₁、F₂，P是两曲线的一个交点，则｜PF₁｜·｜PF₂｜=　　　　　　　 .

7.过点A(-2，4)、B(3，-2)的双曲线的标准方程为　　　　　　　 .

8.与双曲线16x²-9y²=-144有共同焦点，且过点(0，2)的双曲线方程为　　　　　　　 .

三、解答题

9.已知点A(3，0)，圆C：(x+3)²+y²=16，动圆P与圆C相外切并过点A，求动圆圆心P的轨迹方程.

10.在双曲线x²-y²=1上求一点P，使它到直线y=x的距离为.

AA级

一、选择题

1.直线l过双曲线-=1的下方焦点F₁且与双曲线的下支交于A、B两点，F₂是双曲线的另一个焦点，且｜AB｜=m,则△ABF₂的周长为(　　)

A.4a+m　　　　　B.4a+2m　　　　 C.4a-m　　　　　D.4a-2m

2.若曲线x²-y²=a²与曲线(x-1)²+y²=1恰好有三个不同的公共点，则实数a的值只能是(　　)

A.a=0　　　　　　　　　　　 B.a=±1

C.0＜｜a｜＜1　　　　　　　 D.｜a｜＞1

3.若+=1表示双曲线，a为负常数，则m的取值范围是(　　)

A.(,-)　　　　　　　　 B.(,-)

C.(-∞,-)∪(,+∞)　　　D.(- ,)

4.依次连接双曲线x²-y²=12与圆x²+y²=25的交点，则所成的图形是(　　)

A.三角形　　　　　　B.菱形　　　　　C.矩形　　　　　D.正方形

5.斜率为2的直线与双曲线2x²-y²=2交于P、Q两点，则线段PQ的中点M的轨迹方程是(　　)

A.y=x　　　　　　　　　　　　　 B.y=x(｜x｜＞)

C.y=x(｜x｜＞2)　　　　　　 D.y=x(｜x｜≥ )

二、填空题

6.已知B(-5，0)，C(5，0)是△ABC的两个顶点，且sinB-sinC=sinA,则顶点A的轨迹方程是　　　　　　　　　　　.

7.已知双曲线-=1(a＞0,b＞0)的弦AB的中点为M，O为坐标原点，则直线OM和直线AB的斜率的乘积为　　　　　　　　　　　　　　.

8.关于x的方程=x+b没有实数根，则实数b的取值范围是　　　　　　 .

三、解答题

9.已知不论b取何实数，直线y=kx+b与双曲线x²-2y=1总有公共点，试求实数k的取值范围.

10.双曲线3x²-y²=1上是否存在关于直线=2x对称的两点A、B?若存在，试求出A、B两点的坐标；若不存在，说明理由.

【素质优化训练】

1.平面内有一条定线段AB，其长度为4，动点P满足｜PA｜-｜PB｜=3,O为线段AB的中点，则｜OP｜的最小值是(　　)

A.1　　　　　　 B.　　　　　C.2　　　　　　 D.4

2.P为双曲线C上的一点，F₁、F₂是双曲线C的两个焦点，过双曲线C的一个焦点作∠F₁PF₂的平分线的垂线，设垂足为Q，则Q点的轨迹是(　　)

A.直线　　　　B.圆　　　　　C.椭圆　　　　D.双曲线

3.给出下列曲线：①4x+2y-1=0;②x²+y²=3;③+y²=1;④-y²=1，其中与直线y=-2x-3有交点的所有曲线是(　　)

A.①③　　　　B.②④　　　　C.①②③　　　D.②③④

4.若动圆P与两定圆(x+5)²+y²=1及(x-5)²+y²=49都相内切或都相外切，则动圆圆心轨迹方程是(　　)

A. -=1　　　　　　　　　B.-=1(x＞0)

C.-=1　　　　　　　　　　D.-=1(x＞0)

5.已知m,n为两个不相等的非零实数，则方程mx-y+n=0与nx²+my²=mn所表示的示意曲线是(　　)

二、填空题

6.已知双曲线x²-=1,过点P(2，1)作直线交双曲线于A、B两点，并使P为AB的中点，则｜AB｜=　　　　　　　 .

7.若圆C过双曲线-=1的两焦点，且截直线y=-1所得弦长为8，则圆C的方程为　　　　　　　 .

8.过点M(3，-1)且被点M平分的双曲线-y²=1的弦所在直线方程为　　　　　　　 .

三、解答题

9.若双曲线y²-x²=1上的点P与其焦点F₁、F₂的连线互相垂直，求P点的坐标.

10.设k和r是实数，且r＞0，使得：直线y=kx+1既与圆x²+y²=r²相切，又与双曲线x²-y²=r²有两个交点.

(1)求证：-k²=1,且｜k｜≠1;

(2)试问：直线y=kx+1能否经过双曲线x²-y²=4²的焦点?为什么?

【生活实际运用】

活动1：求证直线y=kx+m与双曲线+=1相切的充要条件是：m²=a²·k-b²

若过双曲线上一点P(x₀,y₀)斜率为k的切线为y=kx+y₀-kx₀,其中m=y₀-kx.且b²x²₀-a²b²,联立可解得斜率k= (y≠0),代入切线方程可得过点P(x₀,y₀)双曲线的切线方程为

-=1

特别地，当y₀=0时亦合上面的方程.

活动2：运用上面结论可求过双曲线-=1上一点(x₀,y₀)的切线方程与法线方程，若双曲线方程为-=1时，过曲线上点(x₀,y₀)的切线和法线方程又是怎样?

【知识验证实验】

1.运用双曲线定义解方程｜｜x-3｜-｜x+3｜｜=2.

解：该方程的解是以(-3，0)，(3，0)为焦点，2为实轴长的双轴线与x轴交点的横坐标，其方程为x²-=1，令y=0得x=±1，即原方程的解为x=±1.

2.运用双曲线图形解无理不等式

2＞x+1

解：令y₁=2,y₂=x+1，即x²-=1(y₁≥0),在同一坐标系中画出两图形，使得双曲线的部分在直线部分上方的x的值为原不等式的解.故原不等式的解集为(-∞，-1).

【知识探究学习】

1.设声速为a米/秒，在相距10a米的A、B两监听室中，听到一爆炸声的时间差为6秒，且纪录到B处的声强是A处的4倍，若已知声速a=340米/秒，声强与距离的平方成反比，试确定爆炸点P到AB的中点M的距离.

解：以AB所在直线为x轴，以线段AB的中垂线为y轴，建立直角坐标系，则A(-5a，0)，B(5a,0)，P(x,y)，｜PA｜-｜PB｜=6a，到A、B两点距离差为6a的点在双曲线， -=1(x≥3a)上　　①,

又B处的声强是A处声强的4倍，∴｜PA｜²=4｜PB｜²,即(x+5a)²+y²=4［(x-5a)²+y²］，3x²+3y²-50ax+75a²=0　　②，

由①、②消去y,得25x²-150ax+81a²=0，x=a或x=a(舍去)，y=a，∴｜PM｜==a=340(米)，

答：P点到AB中点M的距离为340米.

2.如图所示，某农场在P处有一肥堆，今要把这堆肥沿道路PA或PB送到大田ABCD中去，已知AP=100m，PB=150m,∠APB=60°，能否在大田中确定一条界线，使位于界线一侧的点沿PA送肥较近，而另一侧的点沿PB送肥较近?如能，请确定这条界线.

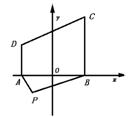
解题思路：大田ABCD中的点分成三类：第一类设PA送肥较近，第二类沿PB送肥较近，第三类沿PA和PB送肥一样远近，第三类构成第一类、第二类点的界线，即我们所要求的轨迹，设以AB所在直线为x轴，AB的中垂线为y轴，建立直角坐标系，设M为界线所在曲线上的一点，则满足｜PA｜+｜AM｜=｜PB｜+｜BM｜,于是｜MA｜-｜MB｜=｜PB｜-｜PA｜=50.可知M点的轨迹是以A、B为焦点的双曲线一支其方程可求得为-=1.(0≤y≤60，25≤x≤35)界线为双曲线在矩形中的一段.

参考答案：

【同步达纲检测】

A级

1.D　2.D 3.C　4.B　5.C 6. -　7.-=1　8. -=1

9.解：设P(x,y),依题意有｜PC｜=｜PA｜+4，∴P点的轨迹是以C(-3，0)，A(3，0)为焦点，且实轴长为4的双曲线的右支、其方程为-=1(x≥2)

10.解：设P(cscθ,cotθ)，则=∴, =±2，∴tan=±2，由万能公式求得P(±,±)

AA级

1.B　2.A 3.B　4.C　5.B 6. -=1(x＜-3)　7. 　8.(-∞,-1)∪［9，1］

9.解：联立方程组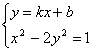消去y得(2k²-1)x²+4kbx+2b²+1=0,依题意有△=(4kb)²-4(2k²-1)(2b²+1)=-4(2k²-2b²-1)＞0，对所有实数b恒成立，∴2k²-1＜0，得-＜k＜

10.解：设AB：y=-x+m,代入双曲线方程得11x²+4mx-4(m²+1)=0,这里△=(4m)²-4×11［-4(m²+1)］=16(2m²+11)＞0　恒成立，设A(x₁,y₁),B(x₂,y₂),AB的中点为M(x₀,y₀,)则x₁+x₂=-，∴x₀=-,y₀=-x₀+m=,若A、B关于直线y=2x对称，则M必在直线y=2x上，∴=-得m=1，由双曲线的对称性知，直线y=-x与双曲线的交点的A、B必关于直线y=2x对称.∴存在A、B且求得A(，-)，B(-，)

【素质优化训练】

1.B　2.B 3.D　4.C　5.C 6.4　7.x²+(y-4)²=41　8.3x+4y-5=0

9.解：设P(x,y),∵F₁(0,-),F₂(0, ),∴=,=,∵·=-1,即x²+y²=1,又y²-x²=1，∴x=±,y=±,∴P的坐标为(，)，(，-)，(-，)和(-，-)

10.解(1)因为直线y=kx+1与圆x²+y²=r²相切，所以有=r,∴=r²,∵r²≠0,∴-k²=1，又由于直线y=kx+1与双曲线x²-y²=r²相交，故交点坐标(x,y)满足方程组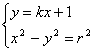,将①代入②得(1-k²)x²-2kx-(1+r²)=0 　 ③,因直线与双曲线有两个交点，且对任意实数k，直线不平行y轴，故③有两个不同的实数根，因此1-k²≠1,∴｜k｜≠1

(2)双曲线x²-y²=r²的过点是F₁(-r,0),F₂(r,0)，若直线y=kx+1过点F₁,则 - rk+1=0,即k=，又由(1)结论-k²=1得k²=1与｜k｜≠1矛质.故直线y=kx+1不可能过双曲线x²-y²=r²的左焦点，同理可得，直线y=kx+1也不可能过双曲线x²-y²=r²的右焦点.