|
|
学科:数学 |
| 教学内容:抛物线及其标准方程 |
【基础知识精讲】
1.定义
平面内与一个定点F和一条定直线l的距离相等的点的轨迹是抛物线.F是焦点,l为准线.圆锥曲线可统一定义为:平面内与一定点F和定直线l的距离之比为常数e的点的轨迹,当0<e<1时,表示椭圆;当e>1时,表示双曲线;当e=1时,表示抛物线.
2.标准方程和图形、焦点坐标及准线方程
| 焦点的位置 | 图 形 | 方程 | 焦点 | 准线 |
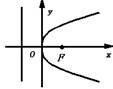
| 焦点在x 正半轴 |
| y2=2px(p>0) | ( | x=- |
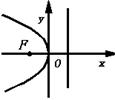
| 焦点在x 负半轴 |
| y2=-2px(p>0) | (- | x= |
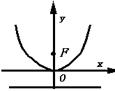
| 焦点在y 正半轴 |
| x2=2py(p>0) | (0, | y=- |
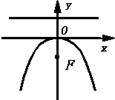
| 焦点在y 负半轴 |
| x2=-2py(p>0) | (0,- | y= |
注:抛物线的标准方程中一次项变量及它的系数的符号决定抛物线的开口方向,其焦点的非零坐标为一次项变量的系数的![]() .
.
3.抛物线的焦半径
抛物线y2=2px(p>0)上任一点M(x0,y0)到焦点的距离等于到准线的距离且为x0+![]() .其它三种不同形式同学们自己给出.
.其它三种不同形式同学们自己给出.
本节学习要求:
学习抛物线及其标准方程,如何利用已知的抛物线方程研究其性质,以及已知某些性质求抛物线的方程是考查的重点.主要方法有轨迹法、定义法、待定系数法等.
本节内容也充满运动变化的思想.学习本节内容要注意如何利用运动变化的观点思考问题,如何利用数学研究运动变化着现实世界,以提高分析问题和解决问题的能力.
【重点难点解析】
1.学习抛物线及其标准方程可以像学习椭圆、双曲线一样从画图开始,也可以直接从第8.2节例4及第8.4节例3引入,这样定义抛物线,便于导出它的标准方程,也可以一开始就看到抛物线和椭圆、双曲线之间的联系.
2.本节重点是抛物线的定义及有关概念、抛物线的四种位置、四种标准方程、焦点坐标、准线方程.难点是分清标准方程的四种不同形式及抛物线的应用.
例1 在抛物线y2=12x上,求与焦点的距离等于9的点的坐标.
分析 由方程y2=12x 得F(3,0),准线l:x=-3,设所求点为P(x,y),则由定义知|PF|=x+3 又|PF|=9
∴x+3=9x=6
代入y2=12x 得 y=±6![]()
故所求点为(6,6![]() ),(6,-6
),(6,-6![]() )
)
例2
已知顶点在原点、焦点在坐标轴上的抛物线被直线l:y=2x+1截得的弦长为![]() ,求抛物线方程:
,求抛物线方程:
分析 (1)设抛物线方程为y2=2ax(a≠0),将y=2x+1代入抛物线方程y2=2ax得
4x2+(4
设两交点为A(x1,y1),B(x2,y2)则
|AB|=![]()
![]()
=![]() =
=![]()
解得a=6或-2.
(2)设抛物线方程为x2=2my(m≠0)
同理求得:m=![]() 或m=-
或m=-![]()
综上所述,所求抛物线方程为
y2=12x,y2=-4x,x2=![]() y,x2=-
y,x2=-![]() y.
y.
【难题巧解点拨】
例1 如果抛物线y2=px和圆(x-2)2+y2=3相交,它们在x轴上方的交点为A、B,那么当p为何值时,线段AB的中点M在直线y=x上?
分析 设交点A、B的坐标分别为(x1,y1),(x2,y2),中点M(x0,y0),把y2=px代入圆方程(x-2)2+y2=3得
x2+(p-4)x+1=0 ∴x1+x2=4-p,x1x2=1
∴x0=![]() =
=![]()
∵A、B在x轴上方
∴y1+y2=![]() =
=![]() =
= ![]()
=![]()
∴y1+y2=![]() ,从而y0=
,从而y0=![]() =
=![]()
![]()
∵点M在直线y=x上 ∴y0=x0
∴![]()
![]() =
=![]()
即 p2-7p+8=0
解得:p=![]()
∵4-p>0
∴p=![]() 不合题意
不合题意
∴p=![]()
例2 过抛物线y2=2px(p>0)的焦点F,引两条相互垂直的弦AC、BD,求四边形ABCD面积的最小值.
分析 AC、BD是焦点弦,又AC⊥BD,故四边形面积 S=![]() |AC|·|BD|.
|AC|·|BD|.
设AC所在的直线方程为y=k(x-![]() ),代入抛物线方程得:
),代入抛物线方程得:
4k2x2-4p(k2+2)x+p2k2=0
且设A(x1,y1),C(x2,y2)
∴|AC|=x1+x2+p=![]()
设BD所在直线方程为y=-![]() (x-
(x-![]() ),
),
且设B(x3,y3),D(x4,y4),由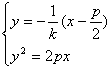 消去y得
消去y得
4(-![]() )2x2-4p[(-
)2x2-4p[(-![]() )2+2]x+p2(-
)2+2]x+p2(-![]() )2=0,则|BD|=x3+x4+p=2p(k2+1).
)2=0,则|BD|=x3+x4+p=2p(k2+1).
∴四边形的面积S=![]() |AC|·|BD|=
|AC|·|BD|=![]() =2p2(2+k2+
=2p2(2+k2+![]() )≥2p2(2+2
)≥2p2(2+2![]() )=8p2.
)=8p2.
当且仅当k2=![]() 即|k|=1,四边形的面积最小,最小值为8p2.
即|k|=1,四边形的面积最小,最小值为8p2.
【典型热点考题】
例1
直线l1和l2相交于M,l1⊥l2,点N∈l1,以A,B为端点的曲线段C上任一点到l2的距离与到点N的距离相等,若△AMN为锐角三角形,|AM|=![]() ,|AN|=3,且|BN|=6,建立适当坐标系,求曲线段C的方程.
,|AN|=3,且|BN|=6,建立适当坐标系,求曲线段C的方程.
分析 建立如图所示直角坐标系,由题意可知曲线段C是以N为焦点,l2为准线的抛物线的一段因此可用待定系数法及它的方程为y2=2px(p>0,待定)(xA≤x≤xB,y>0)其中xA、xB分别为A、B的横坐标,p=|MN|.
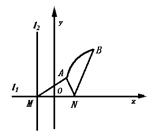
所以M、N的坐标为M(-![]() ,0),N(
,0),N(![]() ,0),由点A在曲线C上,AM=
,0),由点A在曲线C上,AM=![]() ,AN=3,得
,AN=3,得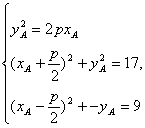
解得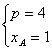 或
或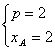
因为△AMN是锐角三角形,∴xA<![]()
∴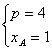
由点B在曲线段C上,得xB=|BN|-![]() =4.
=4.
所以所求的曲线段C的方程是y2=8x(1≤x≤4,y>0).
例2 已知抛物线y2=2px(p>0).过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B,|AB|≤2p.
(Ⅰ)求a的取值范围.
(Ⅱ)若线段AB的垂直平分线交x轴于点N,求Rt△NAB面积的最大值.
分析 (Ⅰ)直线方程为y=x-a,将y=x-a代入y2=2px,得
x2-2(a+p)x+a2=0
设直线l与抛物线两个不同交点的坐标为A(x1,y1),B(x2,y2),
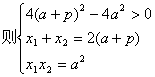
∴|AB|=![]()
![]() =
=![]()
∵0<|AB|≤2p,8p(p+![]() ≤2p,解得-
≤2p,解得-![]() <a≤-
<a≤-![]()
(Ⅱ)设AB的垂直平分线交AB于点Q,令其坐标为(x0,y0),
由中点坐标公式有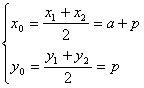
∴|QM|=![]() =
=![]() p
p
又∵△MNQ为等腰直角三角形,
∴|QN|=|QM|=![]() p
p
∴S△NAB=![]() |AB|·|QN|=
|AB|·|QN|=![]() p·|AB|≤
p·|AB|≤![]() p·2p=
p·2p=![]() p2
p2
即△NAB面积的最大值为![]() p2.
p2.

【同步达纲练习】
A级
一、选择题
1.抛物线y=-![]() x2的准线方程是( )
x2的准线方程是( )
A.x=![]() B.x=
B.x=![]() C.y=2 D.y=4
C.y=2 D.y=4
2.直线y=kx-2交抛物线y2=8x于A、B两点,若AB中点的横坐标为2,则k等于( )
A.0 B
3.直线和抛物线有且仅有一个公共点是直线和抛物线相切的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.若点P到点F(4,0)的距离比它到定直线x+5=0的距离小1,则P点的轨迹方程是( )
A.y2=-16x B.y2=-32x C.y2=16x D.y2=32x
5.抛物线y2=2px上横坐标为6的点到焦点的距离是10,则焦点到准线距离是( )
A.4 B
二、填空题
6.抛物线y2=8x关于直线y=x对称的曲线方程是 .
7.抛物线y=4x2上到直线y=4x-5的距离最近的点的坐标是 .
8.P(x1,y1),P2(x2,y2)是过抛物线y2=2px(p>0)的焦点的弦的两端,则y1y2= .
三、解答题
9.已知抛物线y=ax2-1上恒有关于直线x+y=0对称的相异两点,求a的取值范围.
10.已知A、B是抛物线y2=2px(p>0)上的两点,且OA⊥OB(O为坐标原点),求证:(1)A、B两点的横坐标之积为定值;(2)直线AB经过定点.
AA级
一、选择题
1.已知P(x0,y0)是抛物线y2=2mx上的任意一点,则点P到焦点的距离是( )
A.|x0-![]() |
B.|x0+
|
B.|x0+![]() |
|
C.|x0-m| D.|x0+m|
2.过抛物线的焦点F的直线与抛物线交于A、B两点,若A、B两点在抛物线的准线上的射影是A1、B1,则∠A1FB1等于( )
A.45° B.60° C.90° D.°120
3.过抛物线y2=4x的焦点F作直线,交抛物线于A(x1,y1)、B(x2,y2)两点,若x1+x2=6,则|AB|等于( )
A.4 B.6 C.8 D.10
4.动点P在曲线y=2x2+1上移动,则点P和定点A(0,-1)连线的中点的轨迹方程是( )
A.y=2x2 B.y=4x2 C.y=6x2 D.y=8x2
5.F是抛物线y2=2x的焦点,P是抛物线上任一点,A(3,1)是定点,则|PF|+|PA|的最小值是( )
A.2 B.![]() C.3 D.
C.3 D.![]()
二、填空题
6.若(4,m)是抛物线y2=2px上的一点,F是抛物线的焦点,且|PF|=5,则抛物线的方程是 .
7.抛物线y2=2x上的两点A、B到焦点F的距离之和是5,则线段AB的中点M的横坐标是 .
8.若抛物线y2-mx-2y+4m+1=0的准线与双曲线![]() -
-![]() =1的右准线重合,则m的值是 .
=1的右准线重合,则m的值是 .
三、解答题
9.已知椭圆![]() +y2=1的焦点为F1、F2,抛物线y2=px(p>0)与椭圆在第一象限的交点为Q,若∠F1QF2=60°,(1)求△F1QF2的面积;(2)求此抛物线的方程.
+y2=1的焦点为F1、F2,抛物线y2=px(p>0)与椭圆在第一象限的交点为Q,若∠F1QF2=60°,(1)求△F1QF2的面积;(2)求此抛物线的方程.
10.已知直线l过原点,抛物线C的顶点在原点,焦点在x轴的正半轴上,若A(-1,0),B(0,8)关于直线l对称的点都在C上,求直线l和抛物线C的方程.
【素质优化训练】
一、选择题
1.抛物线y=2ax2(a≠0)的焦点坐标是( )
A.( ![]() ,0) B.(0,
,0) B.(0,
![]() ) C.(
) C.(
![]() ,0) D.(0,
,0) D.(0,
![]() )
)
2.长度为4的线段AB的两个端点A、B都在抛物线x2=4y上,则线段AB的中点M的纵坐标的最小值为( )
A. ![]() B.1 C.2 D.4
B.1 C.2 D.4
3.抛物线y=x2上到直线2x-y-4=0最近的点的坐标是( )
A.(![]() ,
,![]() ) B.(1,1) C.(
) B.(1,1) C.(![]() ,
,![]() ) D.(2,4)
) D.(2,4)
4.已知抛物线y2=2px(p>0)上有一点M(4,y),它到焦点F的距离为5,则△OFM的面积(O为原点)为( )
A.1 B.
![]() C.2 D.2
C.2 D.2![]()
5.若点P在抛物线y2=x上,点Q在圆(x-3)2+y2=1上,则|PQ|的最小值等于( )
A.![]() -1 B.
-1 B.![]() -1 C.2 D.
-1 C.2 D.![]() (
(![]() -2)
-2)
二、填空题
6.已知抛物线y2=4ax(a>0)上一点A(m,n)到焦点F的距离为4a,则m= ,n= .
7.抛物线y2=16x上的一点P到x轴的距离为12,则P与焦点F间的距离|PF|= ;
8.定点A(3,2)是抛物线y2=2px(p>0)内部的一点,F是抛物线的焦点,点Q在抛物线上移动,已知|AQ|+|QF|的最小值为4,则P= .
三、解答题
9.设抛物线y2=2px(p>0)的弦PQ交x轴于点R,过P、Q分别作x轴的垂线,垂足分别为M、N,求证:|OR|是|OM|和|ON|的等比中项.
10.设抛物线C:y2=2px(p>0)上有两动点A、B(AB不垂直于x轴),F为焦点,且|AF|+|BF|=8,又线段AB的垂直平分线恒过定点Q(6,0).(1)求抛物线C的方程;(2)求△AQB的面积最大值.
【生活实际运用】
1.证明直线y=kx+m与抛物线y2=2px相切的充要条件是m=![]() .
.
2.过抛物线y2=2px上一点P(x0,y0)的切线方程为 .
提示:用上题结论y=kx+m=kx+y0-kx0.
m=![]() =y0-kx0
=y0-kx0![]() k=
k=![]()
3.某隧道横断面由抛物线拱顶与矩形三边组成,尺寸如图.某卡在空车时能过此隧道,现载一集装箱,箱宽3米,车与箱共高4.5米,此车能否通过此隧道,说明理由.
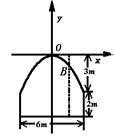
分析 车隧道横断面(如图)进行研究,关键是看在离隧道中心线1.5米处,隧道顶高是否有4.5米,(这只是理论上的研究,实际通过时还应留有余地)适当建立直角坐标系,利用抛物线的标准方程,会使计算更方便一些.
如图建立直角坐标系.设抛物线标准方程为x2=-2py,则点(3,-3)在抛物线上,求得P=![]() ,上拱抛物线方程为x2=-3y,箱宽3米,故当x=1.5米时,y=-0.75米即B(1.5,-
,上拱抛物线方程为x2=-3y,箱宽3米,故当x=1.5米时,y=-0.75米即B(1.5,-![]() ),那么B点到底的距离为5-0.75=4.25米
),那么B点到底的距离为5-0.75=4.25米
而车与箱的高为4.5米,故不能通过.
【知识验证实验】
抛物线y2=2x上的点P(x,y)到点A(a,0)(a∈R)的距离的最小值记为f(a).
(1)求f(a)的表达式;
(2)当![]() ≤a≤5时,求f(a)的最大值和最小值.
≤a≤5时,求f(a)的最大值和最小值.
分析 (1)|PA|=![]() =
=![]() =
=![]()
当a-1<0,即a<1时,f(a)=|a|,当a-1≥0,即a≥1时,f(a)= ![]() .
.
∴f(a)= 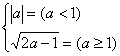
(2)当![]() ≤a≤5时
≤a≤5时
fmin=f(![]() )=
)=![]()
fmax=f(5)=3.
解:(1)|PA|=![]() =
=![]() =
=![]() ,当a-1<0,即a<1时,f(a)=|a|,当a-1≥0,即a≥1时,f(a)=
,当a-1<0,即a<1时,f(a)=|a|,当a-1≥0,即a≥1时,f(a)= ![]() ,∴f(a)=
,∴f(a)= 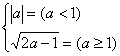
(2)当![]() ≤a≤5时,①若a∈[
≤a≤5时,①若a∈[![]() ,1],f(a)=a为[
,1],f(a)=a为[![]() ,1]上的增函数.∴fmin=f(
,1]上的增函数.∴fmin=f(![]() )=
)=![]() ,②若a∈[1,5],f(a)=
,②若a∈[1,5],f(a)= ![]() 为[1,5]上增函数,∴fmax=f(5)=
为[1,5]上增函数,∴fmax=f(5)=
![]() =3,综上知:f(a)的最大值为3,最小值为
=3,综上知:f(a)的最大值为3,最小值为![]() .
.
【知识探究学习】
1.求证:以抛物线的焦点弦为直径的圆必与抛物线的准线相切.
若将抛物线换成椭圆、双曲线,结论又如何.
2.防空探照灯的反射镜与过轴的截面的交线是一条抛物线.已知灯口直径是2000mm,深度是800mm.光源应放在什么位置?
答:光源应放在反光曲面轴上距顶点312.5mm处.

参考答案:
【同步达纲练习】
A级
1.C 2.C 3.B
4.C 5.B 6.x2=8y 7.( ![]() ,1) 8.-p2
,1) 8.-p2
9.解:设在抛物线y=ax2-1上关于直线x+y=0对称的相异两点为P(x,y),Q(-y,-x),则
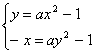
![]() ,由①-②得x+y=a(x+y)(x-y),∵P、Q为相异点,∴x+y≠0,又a≠0,∴x-y=
,由①-②得x+y=a(x+y)(x-y),∵P、Q为相异点,∴x+y≠0,又a≠0,∴x-y=![]() ,即y=x-
,即y=x-![]() ,代入②得a2x2-ax-a+1=0,其判别式△=a2+ra2(a-1)>0,解得a>
,代入②得a2x2-ax-a+1=0,其判别式△=a2+ra2(a-1)>0,解得a>![]() .
.
10.解:(1)设A(2pt21,2pt1),B(2pt22,2pt2),由OA⊥OB得kOA·kOB=![]() ·
·![]() =-1,∴t1t2=-1,∴A、B两点的横坐标之积为2pt21·2pt22=4p2为定值.
=-1,∴t1t2=-1,∴A、B两点的横坐标之积为2pt21·2pt22=4p2为定值.
(2)AB的方程为![]() =
=![]() ,即(t1+t2)y=x+2pt1t2,将t1t2=-1代入得(t1+t2)y=x-2p,表示过定点(2p,0)的直线系,故直线AB过定点(2p,0).
,即(t1+t2)y=x+2pt1t2,将t1t2=-1代入得(t1+t2)y=x-2p,表示过定点(2p,0)的直线系,故直线AB过定点(2p,0).
AA级
1.B 2.C 3.C 4.B 5.B 6.y2=4x 7.2 8.m=4
9.解:(1)在△F1QF2中,|F1F2|2=|QF1|2+|QF2|2-2|QF1||QF2|cos60°=(|QF1|+|QF2|)2-3|QF1||QF2|,而易知![]() ,
,![]() ∴
∴![]() ∴
∴![]() =
=![]() ·
·![]() sin60°=
sin60°=![]()
(2)设Q(x0,y0),(x0>0,y0>0),∵![]() =
=![]() |F1F2|·y0=
|F1F2|·y0=![]() ·2
·2![]() y0=
y0=![]() ,∴y0=
,∴y0=![]() ,又
,又![]() +y20=1,∴x0=
+y20=1,∴x0=![]() (负值舍去),将Q点坐标代入抛物线y2=2px得,(
(负值舍去),将Q点坐标代入抛物线y2=2px得,(![]() )2=2P·
)2=2P·![]()
![]() ,∴p=
,∴p=![]() ,∴抛物线的方程为y2=
,∴抛物线的方程为y2=![]() x.
x.
10.解:设直线l的方程为y=kx,抛物线方程为y2=2px(p>0),A、B关于l的对称点分别为A′(x1,y1),B′(x2,y2),则AA′⊥l,∴![]() ·k=-1,BB′⊥l,∴
·k=-1,BB′⊥l,∴![]() ·k=-1,又
·k=-1,又![]() 的中点在l上,BB′的中点在l上,∴
的中点在l上,BB′的中点在l上,∴![]() =k
=k![]() ,
,![]() =·
=·![]() ,又A′、
,又A′、![]() 在抛物线上,∴y21=2px1,y22=2px2,联立以上6个方程解得,p=
在抛物线上,∴y21=2px1,y22=2px2,联立以上6个方程解得,p=![]() ,k=
,k=![]() ,∴所求直线方程为y=
,∴所求直线方程为y=![]() x,抛物线方程为y2=
x,抛物线方程为y2=![]() x
x
【素质优化训练】
1.D 2.B 3.B
4.C 5.D 6.m=3a,n=±2![]() a 7.13 8.2
a 7.13 8.2
9.证明:设R(r,0),PQ:y=k(x-r)(当k不存在时,PQ⊥x轴,则|OR|=|OM|=|ON|,结论成立),由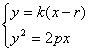 消去y得k2x2-(2k2r+2p)x+k2r2=0,设P(x1,y1),Q(x2,y2),则OM·ON=x1x2=r2,∴|OR|2=|OM|·|ON|,即|OR|是|ON|的等比中项
消去y得k2x2-(2k2r+2p)x+k2r2=0,设P(x1,y1),Q(x2,y2),则OM·ON=x1x2=r2,∴|OR|2=|OM|·|ON|,即|OR|是|ON|的等比中项
10.解:(1)设A、B两点的坐标分别为(x1,y1),(x2,y2),(x1≠x2),则|AF1|=x1+![]() ,BF=x2+
,BF=x2+![]() ,由|AF|+|BF|=8得,x1+x2=8-p ①,
,由|AF|+|BF|=8得,x1+x2=8-p ①,
∵线段AB的垂直平分线恒过定点Q,∴|AQ|=|BQ|,即(x1-6)2+y12=(x2-6)2+y22,将y12=2px1,y22=2px2代入可得x21-x22-(12-2p)(x1-x2)=0,由x1≠x2,∴x1+x2=12-2p ②,
由①②得:p=4,∴抛物线方程为y2=8x.
(2)由(1)知AB中点的横坐标为2,因为(1)得出x1+x2=12-2p,将p=4代入得x1+x2=4,设AB中点的纵坐标为y0,则
kAB=![]() =
=![]() ,∴AB直线的方程为y-y0=
,∴AB直线的方程为y-y0=![]() (x-2),将y2=8x代入AB方程,得y2-2y0y+2y20-16=0.由△>0得-4<y0<4,且y1+y2=2y0,y1y2=2y20-16,∴|AB|=
(x-2),将y2=8x代入AB方程,得y2-2y0y+2y20-16=0.由△>0得-4<y0<4,且y1+y2=2y0,y1y2=2y20-16,∴|AB|=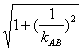
![]() =
=![]()
![]() 点Q到AB的距离d=
点Q到AB的距离d=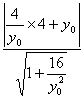 =
=![]() ,∴S△AQB=
,∴S△AQB=![]() |AB|d=
|AB|d=![]()
![]() =
=![]()
![]() ≤
≤![]() .当且仅当16+y20=32-2y20,即y0=±
.当且仅当16+y20=32-2y20,即y0=±![]() 时等号成立,∴△AQB面积最大值为
时等号成立,∴△AQB面积最大值为![]() .
.