高二下 9.1 平面同步练习
基础练习
1．判断下列命题是否正确，并说明理由．
（1）一个平面的面积是
；
（2）平面内的一条线段把这平面分成两部分；
（3）两个平面a 和b 是可能有且只有一个公共点的；
（4）四边形一定是平面图形；
（5）同一平面内不重合的两条直线最多有一个交点；
（6）如果一条直线l在平面a 外，那么这条直线与平面是没有公共点．
2．填空：（平面ABEF记作a ，平面ABCD记作b ，依图9－1填写）
（1）A∈a，B_____ a，E_____ a，C_____ a ，D_____a ；
（2）A∈b，B_____ b，C_____ b，D_____ b，E_____b，F_____ b；
（3）
＝_________；
（4）AB______ a ，AB_____ b，CD_____ a ，CD_____ b，AE_____ b，AE_____ b．
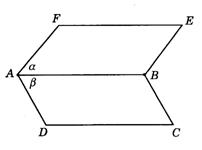
图9－1
3．用符号表示下列语句，并画出图形：
（1）直线l经过平面a 内两点A、B；
（2）直线l在平面a 外，且过平面a 内一点P；
（3）直线l在平面a 内，又在平面b 内；
（4）直线l是平面a与b的交线，平面a内一条直线m与l平行．
4．填空：
（1）要判断一条直线在某一平面内，只要判断这条直线上的_________个点在此平面内．
（2）要寻找两个平面的公共点，应该在这两个平面的__________上去找．
（3）“确定一个平面”的含义是__________________．
5．用符号表示下列各命题的结论：
（1）若A∈a，A∈b，＝l，则______________；
（2）若A∈a，B∈a，A∈b，B∈b，则___________；（其中a、b 不重合）
（3）若a
a，ab，则___________；（其中a、b不重合）
（4）若ABa，C∈AB，则___________；
（5）若PQ
a，P∈a，则___________．
6．下列命题中正确的是（ ）．
A．经过三点确定一个平面 B．经过一条直线和一个点确定一个平面
C．经过两条直线确定一个平面 D．两两相交且不共点的三条直线确定一个平面
7．三条相交直线最多可以确定（ ）．
A．一个平面 B．两个平面 C．三个平面 D．四个平面
8．四条平行直线最多可以确定（ ）．
A．三个平面 B．四个平面 C．五个平面 D．六个平面
综合练习
1．下列空向图形中的实线、虚线的使用是否正确?请把其中不正确的地方改过来：
（1）平面a 在平面b 的前方．
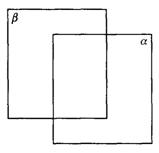
图9－2－1
（2）直线l与平面a 相交于点A．
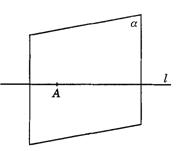
图9－2－2
（3）平面a、b 相交于AB，平现b、g 相交于CD，直线l与平面a 相交于E，直线l与平面g 相交于F．
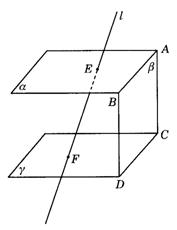
图9－2－3
2．用符号表示下列语句，并画出图形：
（1）直线l过平面a 内一点A，且过a 外两点B、C；
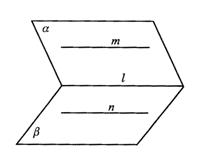
（2）平面a 与b 的交线为l，直线m在a 内，直线n在b 内，且m、n与l分别交于P、Q点；
（3）平面a 与b 相交于直线l，直线m在a 内，直线n在b 内，且m、n都与l平行．
3．空间四点A、B、C、D，如果其中任意三点不共线，则经过其中三个点的平面有（ ）．
A．一个或两个 B．一个或三个 C．一个或四个 D．两个或三个
4．若直线上有两个点在平面外，则（ ）．
A．直线上至少有一个点在平面内 B．直线上有无穷多个点在平面内
C．直线上所有点都在平面外 D．直线上至多有一个点在平面内
5．如图9－3，平面a 
平面b ＝l，A∈a，B∈a，ABl＝D，C∈b ，且C
l，则平面ABC与平面a 的交线是（ ）．
A．直线AC B．直线AB C．直线CD D．直线BC
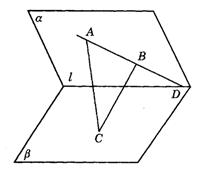
图9－3
6．在空间中，下列命题中正确的是（ ）．
A．对边相等的四边形一定是平面图形
B．四边相等的四边形一定是平面图形
C．有一组对边平行且相等的四边形是平面图形
D．有一组对角相等的四边形是平面图形
7．如图9－4，平面a平面b ＝l，直线aa，且a与l不平行，在b 内作直线b，使a、b相交．
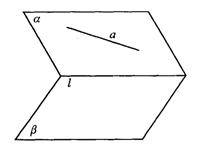
图9－4
8．如图9－5，已知△ABC及平面a，ABa＝P，BCa＝Q，求作直线AC与平面a的交点M．
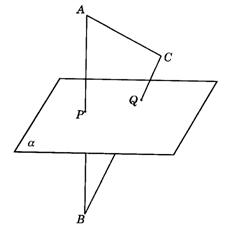
图9－5
9．已知a、b是两条直线，且a∥b，又A∈a，B∈a，C∈b，D∈b．判断直线AC、AD、BC、BD是否在同一个平面内，并说明理由．
10．如图9－6，平面a平面b＝l，aa，bb，ab＝P，判断点P是否在直线l上，并说明理由．
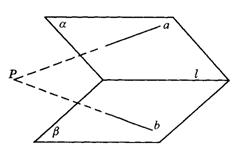
图9－6
11．如图9－7，△ABC在平面a 外，其三边所在直线分别与a 交于P、Q、R三点，判断P、Q、R三点是否共线，并说明理由．
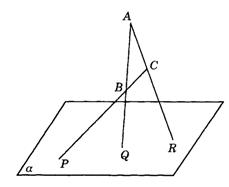
图9－7
12．如图9－8，四条直线a、b、c、d两两相交于M、N、P、Q、R、S六个点，判断a、b、c、d是否共面，并说明理由．
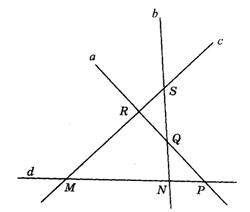
图9－8
13．三个平面两两相交，若交线记为a、b、c．若a、b、c中任意两条都不平行，求证：a、b、c必相交于一点．
14．在正方体ABCD－
中，E是棱
的中点，由三点A、
、E确定的平面记作a．
（1）试判断平面ABCD与平面a有多少个公共点；
（2）平面ABCD与平面a的所有公共点构成什么图形?
（3）画出符合题意的图形，并把（2）中构成的图形画出来．
参考答案
基础练习
1．（1）不正确．因为平面是无限延展的，没有面积．
（2）不正确．平面内的线段不能形成对平面的分割．
（3）不正确．平面a、b 若有公共点，则一定相交于过此点的一直线．
（4）不正确．四边形可能是空间图形．
（5）正确．由平面几何知识知，不重合的两条直线的位置关系是平行与相交，若相交，交点唯一．
（6）不正确．直线l可能与平面a有一个公共点，l上其余各点均在a外．
2．（1）B∈a，E∈a，Ca，Da；
（2）B∈b，C∈b，D∈b，Eb，Fb；
（3）a∩b＝AB；（4）ABa，ABb，CD
a，CDb，AEa，AEb；
3．（1）A∈a，B∈a，A∈l，B∈l．（如图答9－1）
（2）la，P∈l，P∈a．（如图答9－2）．
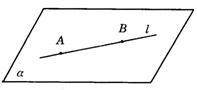
图答9－1
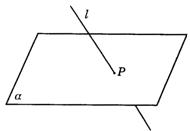
图答9－2
（3）la，lb．（如图答9－3）
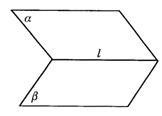
图答9－3
（4）a∩b＝l，ma，m∥l．（如图答9－4）
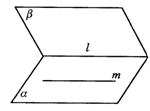
图答9－4
4．（1）两．
（2）交线．
（3）有且只有一个平面．
5．（1）A∈l（根据公理2）．
（2）a∩b＝AB（根据公理2）．
（3）a∩b＝a （根据公理2）．
（4）C∈a（根据公理1）．
（5）Q
a（根据公理1，如图答9－5）．
6．D 若三点共线，则此三点不能确定一个平面，故A不正确．若点在直线上，则此直线和点不能确定一个平面，故B不正确．空间两条直线若异面，则这两直线不在任何平面内，故C不正确．
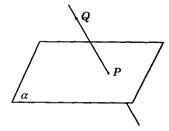
图答9－5
7．C．
8．D．
综合练习
1．（1）不正确，改为
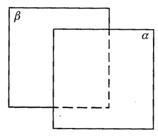
图答9－2－1
（2）不正确，改为
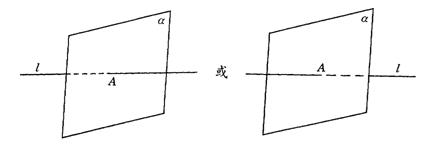
图答9－2－2
（3）不正确，改为
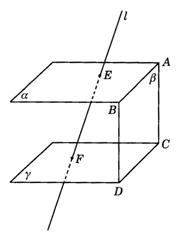
图答9－2－3
2．（1）A∈a，Ba，Ca，A∈l，B∈l，C∈l（图答9－6）．
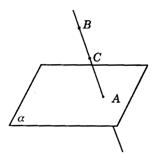
图答9－6
（2）a∩b＝l，ma，nb，m ∩ l＝P，n∩ l＝Q（图答9－7）．
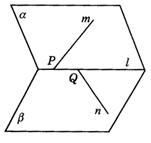
图答9－7
（3）a∩b＝l，ma，nb，m∥l，n∥l（图答9－8）．
图答9－8
3．C．当A、B、C、D共面时，确定一个平面ABCD；当A、B、C、D不共面时，每三个点不共线，可确定一个平面，故可确定四个平面．
4．D．根据公理1判断，并参看图答9－6．
5．B．A、B是平面a 与平面ABC的公共点，故直线AB是两个平面的交线．
6．C．对边平行则保证该四边形是平面图形；又符合平行四边形的判定定理，故选C，其余各选择项均不能保证共面．
7．因为a与l共面但不平行，所以a与l相交，设a∩l＝P，则P∈b，任取Q∈b，但Ql，连结PQ，则直线PQ∩a＝P，所以PQ即为所求的直线b．
8．M∈AC，则M∈平面ABC，故M是平面ABC与平面a 的公共点，因为PQ＝平面
，所以M∈PQ．连结PQ，直线PQ与直线AC的交点即为所求的点M．
9．AC、AD、BC、BD四条直线共面．因为a∥b，所以过a，b有一个平面a．因为A∈a，B∈a，则
A∈a，B∈a，同理C∈a，D∈a．由公理1可知ACa，ADa，BCa，BDa．
10．因为
＝P，所以P∈a，P∈b，又由aa，则P∈a．同理P∈b，则P是a 与b 的公共点．因为＝l，由公理2可知P∈l．
11．P、Q、R三点共线．∵ AB ∩a＝Q，∵
Q∈平面a，∵
AB平面ABC，∵ Q∈平面ABC，∴
Q是平面ABC与平面a 的公共点，同理R也是平面ABC与平面a的公共点，由公理2可知，QR＝，又P也是平面ABC与a 的公共点，由公理2知P∈直线QR，故P、Q、R三点共线．
12．a、b、c、d四线共面．
∵ 
，∴过a、b有一个平面，设为a，∵ aa，ba，又R∈a，P∈a，S∈b，N∈b，∴ R∈a，P∈a，S∈a，N∈a．∴
直线RS
a，PNa，即ca，da，于是a、b、c、d共面于a．
13．对于平面a、b、g
，设＝a，
＝c，
＝b．由a
b，且aa，ba，故a∩b＝A．又A∈ab，A∈b∩g，故A∈c．因此a、b、c相交于同一个点．
14．（1）由于这两个平面有公共点A，故它们有无数个公共点．
（2）所有的公共点构成一条直线．
（3）在平面
中，直线CB与
必相交，设交点F，那么直线AF是所求的图形．