直线和圆的方程单元达标检测(AA级)

	学科：数学
	教学内容：直线和圆的方程单元达标检测(AA级)

【同步达纲练习】

(AA级　提高级)

一、选择题(3′×12)

1.若点P(a,b)在第三象限，则P点到y轴的距离是(　　)

A.-a　　　　　　B.-b　　　　　　C.a　　　　　　 D.b

2.三条直线x+y-2=0，3x-y-3=0，4x-ky+1=0相交于一点，则k的值为(　　)

A.-8　　　　　　B.　　　　　　C.8　　　　　　 D.7

3.结出下面四个命题

①设直线L₁和L₂的斜率分别是k₁,k₂，则L₁和L₂的夹角θ=arctan

②直线x+y-1=0的倾斜角是arctan(-);

③已知三点A(a+b,c).B(b+c,a),C(a+c,b),则A、B、C三点共线

④两平行直线A₁x+B₁y+C₁=0与A₂x+B₂y+C₂=0之间的距离是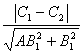，其中正确命题的个数是(　　)

A.0个　 　　　　B.1个　　　　　 C.2个　　　　　 D.3个

4.已知直线L₁和L₂的夹角平分线为y=x，如果L₁的方程是ax+by+c=0(ab＞0)，那么L₂的方程是(　　)

A.bx+ay+c=0　　　　　　　　　　 B.ax-by+c=0

C.bx+ay-c=0　　　　　　　　　　 D.bx-ay+c=0

5.与直线2x-y+4=0的夹角为45°且与这直线的交点恰好在x轴上的直线方程是(　　)

A.x-2y+2=0　　　　　　　　　B.3x+y+6=0

C.x-3y+2=0或3x-y+6=0　　　 D.x-3y+2=0或3x+y+6=0

6.连结A(-4，1)和B(2，5)两点的直线与直线x+y-3=0交于E点，则点B分的比是(　　)

A.- 　　　　　B. 　　　 C.- 　　　　　D.-

7.过点A(2，1)的所有直线中，距离原点最远的直线方程是(　　)

A.x=2　　　　　　　　　　　 B.x-2y+5=0

C.2x+y+5=0　　　　　　　　　D.2x+y-5=0

8.如果把直线x-2y+λ=0向左平移1个单位，直向下平移2个单位，使圆x²+y²+2x-4y=0与它相切，则实数λ的值是(　　)

A.-13或13　　　　　　　　　B.13或-3

C.13或3　　　　　　　　　　D.-13或-3

9.已知点(x₀,y₀)是圆x²+y²=r²外一点，则直线x₀x+y₀y=r²与这个圆的位置关系是(　　)

A.相交　　　　　B.相切　　　C.相离　　　 D.不能确定

10.曲线f(x,y)=0关于直线x-y-2=0的对称曲线的方程为(　　)

A.f(y+2,x)=0　　　　　　　　B.f(x-2,y)=0

C.f(y+2,x-2)=0　　　　　　　D.f(y-2,x+2)=0

11.与圆C：(x-1)²+y²=36同心圆，且面积等于圆C的面积的一半的圆的方程是(　　)

A.(x-1)²+y²=18　　　　　　　 B.(x-1)²+y²=9

C.(x-1)²+y²=6　　　　　　　　D.(x-1)²+y²=3

12.已知两个圆C₁:x²+y²=1和C₂：(x+5)²+y²=1，如果直线x-y+m=0恰好在这两个圆之间通过，则实数m的取值范围是(　　)

A.(1，4)　　　　B.(2，3)　　　　C.(1，3)　　　　D.(2，4)

二、填空题(4′×4)

13.不等式组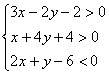的整数解为　　　　　　 .

14.已知P(3，0)是圆x²+y²-8x-2y+12=0内一点，则过P点的最短弦所在直线的方程是　　　　　　 .

15.已知(x-1)²+(y+2)²=4，则的取值范围是　　　　　　 .

16.若实数x,y满足x²+y²-2x+4y=0，求x-2y的最大值是　　　　　　 .

三、解答题

17.如果一个圆与圆x²+y²-2x=0外切，并与直线x+y=0相切于点M(3，-)，求这个圆的方程.(8′)

18.已知以C(2，0)为圆心的圆C和两条射线y=±x，(x≥0)都相切，设动直线L与圆C相切，并交两条射线于A、B，求线段AB中点M的轨迹方程.(10′)

19.求过已知圆x²+y²-4x+2y=0，x²+y²-2y-4=0的交点，且圆心在直线2x+4y=1上的圆的方程.(10′)

20.直线L过点M(2，3)，且被3x+4y-7=0与3x+4y+8=0截得的线段之长为3，求直线L的方程.(10′)

21.某家俱公司生产甲、乙两种型号的组合柜，每种柜的制造白坯时间、油漆时间及有关数据如下：(10′)

工艺要求	产品甲	产品乙	生产能力/(台/天)
制白坯时间/天	6	12	120
油漆时间/天	8	4	64
单位利润/元	20	24

参考答案:

【同步达纲练习】

AA级

一、1.A　2.C  3.B　4.A　5.D  6.C　7.D　8.C  9.A　10.C　11.A　12.B

二、13.(2，1)，(1，0)，(2，0)，(1，-1)，(2，-1)，(3，-1)  14.x+y-3=0　15.［-，0］　16.10

17.设所求圆的圆心是C(a,b)，则过m，c的直线与x+y=0垂直

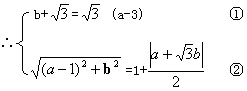
由①②可得，a=0,b=-4或a=4,b=0相应半径为6和2.

∴圆的方程为：x²+(y+4)²=36或(x-4)²+y²=4.

18.设直线L的方程为y=kx+b.A(x₁,y₁),B(x₂,y₂),M(x,y)由得A(, ),(k≠0)

由得B(,)，∴

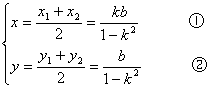
由①②得：k=,b=　③

∵圆C与都相切

∴圆C的半径r=.

∵AB：kx-y+b=0与圆C相切，

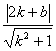∴= ,即2k²+4kb+b²-=0　④

将③代入④　(y²-x²)+4x(y²-x²)-2(y²-x²)=0

∵y²≠x²，∴y²-x²+4x-2=0即(x-2)²-y²=2.(y≠0)

当L⊥x轴时，线段AB的中点M(2±，0)也合上面的方程，其轨迹在∠AOB内

19.设过已知圆交点的圆系方程为：x²+y²-4x+2y+λ(x²+y²-2y-4)=0(λ≠-1)，即(1+λ)x²+(1+λ)y²-4x+(2-2λ)y-4λ=0

圆心(,)又圆心在直线2x+4y=1上

∴

所求圆的方程为：12x²+12y²-20x-4y-28=0

20.略 解：x-7y+19=0或7x+y-17=0

21.设x,y分别为甲、乙二种柜的日产量，可将此题归纳为如下线性规划模型f_max=20x+24y

其中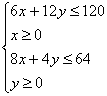由图及下表

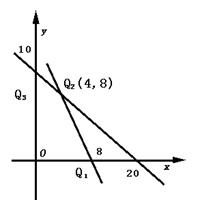
(x,y)	f=20x+24y
(0，10)	240
(0，0)	0
(8，0)	160
(4，8)	72

∴f_max=272

答：该公司安排甲、乙二种柜的日产量分别为4台和8台可获最大利润272元.