直线与平面垂直的判定和性质（三）
1．已知P为△ABC所在平面外一点，点P在平面ABC上的射影为O．
（1）若PA=PB=PC，则O是△ABC的________心；
（2）若PA、PB、PC与平面ABC所成的角相等，则O是△ABC的________心；
（3）若O在△ABC内，且P到△ABC三边的距离相等，则O为△ABC的________ 心；
（4）若PA⊥BC，PB⊥CA，则O为△ABC的________心．
2．在△ABC中，∠ACB=90°，CD⊥平面ABC．求证：△ABD是锐角三角形．
3．已知D为平面ABC外一点，且DA、DB、DC两两垂直．求证：顶点D所对的三角形面积的平方等于其余三个三角形面积的平方和，即
．
4．已知斜线AB和平面a 所成的角为
，BC
a ，BC与AB所成的角为q，BC与AB在平面a 内的射影所成的角为
，求证：
．
5．如图9-33，在△ABC中，∠ABC=90°，SA⊥平面ABC，点A在SB、SC上的射影分别为P、Q．求证：PQ⊥SC．
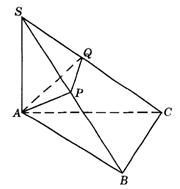
图9-33
6．如图9-34，在△ABC中，∠ACB=90°，AB平面a ，点
，C在a 内的射影为O，AC和BC与平面a 所成的角分别为30°和45°，CD是△ABC的AB边上的高线，求CD与平面a 所成角的大小．
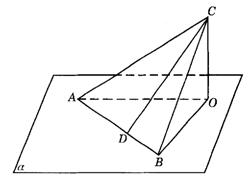
图9-34
参考答案
1．（1）外心．∵ PA=PB=PC，∴ OA=OB=OC，∴ O是△ABC的外心．
（2）外心．PA与平面ABC所成的角为∠PAO，在△PAO、△PBO、△PCO中，PO是公共边，∠POA=∠POB=∠POC=90°，∠PAO=∠PBO=∠PCO，∴ △PAO≌△PBO≌△PCO，∴ OA=OB=OC，∴ O为△ABC的外心．
（3）内心．作OD⊥AB于D，OE⊥BC于E，OF⊥AC于F，连结PD、PE、PF．∵ PO⊥平面ABC，∴ OD、OE、OF分别为PD、PE、PF在平面ABC内的射影，由三垂线定理可知，PD⊥AB，PE⊥BC，PF⊥AC．由已知PD=PE=PF，得OD=OE=OF，∴ O是△ABC的内心．（如图答9-23）
（4）垂心．
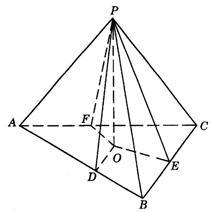
图答9-23
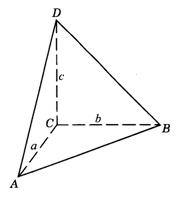
2．如图答9-24，设AC=a，BC=b，CD=c，∵ △ACD是Rt△，∴ 
． ∵ △ABC是Rt△，∴ 
．∵ △BCD是Rt△，∴ 
．而在
△ABD中，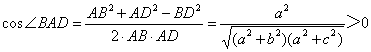
，又∵ ∠BAD是三角形内角，∴
0°＜∠BAD＜180°，∴ ∠BAD是锐角，同理∠ABD、∠ADB是锐角，∴
△ABD是锐角三角形．
图答9-24
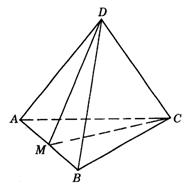
3．如图答9-25，设DA=a，DB=b，DC=c，则
，
，
．在△ABD中，作DM⊥AB于M，则
． ∵ CD⊥AD，CD⊥DB，∴
CD⊥平面ADB，∴
CD⊥DM．在Rt△CDM中，
， ∴ 
图答9-25
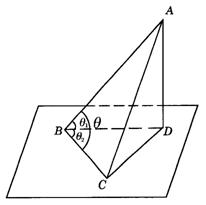
4．如图答9-26，过A作AD⊥a ，垂足为D，连结BD，则
，
，∠ABC=q ．过D作DC⊥BC于C，连结AC，由三垂线定理，AC⊥BC．在Rt△ABC中，
；在Rt△ABD中，
；在Rt△BCD中，
，∴ 
图答9-26
5．
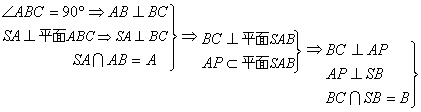
6．连结OD，∵ CO⊥平面AOB，∴
∠CDO为CD与平面a 所成的角．∵ AB、CB与平面a 所成角分别为30°和45°，∴
∠CAO=30°，∠CBO=45°．设CO=a，则AC=2a，OB=a，
．在Rt△ABC中，
，∴ 
． ∵ CD⊥AB，∵
，∴ 
．在Rt△COD中，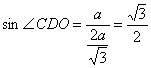
，∵ 0°＜∠CDO＜90°，∴ ∠CDO=60°，即CD与平面a 所成的角为60°．