直线与平面垂直的判定和性质（一）

直线与平面垂直的判定和性质（一）

　　1．下列命题中正确的是（　）．

　　A．若一条直线与平面内的一条直线垂直，则这直线与这个平面垂直

　　B．若一条直线与平面内的两条直线垂直，则这直线与这个平面垂直

　　C．若一直线与平面内的无数条直线垂直，则这直线与这个平面垂直

　　D．若一直线与平面内的任意一条直线都垂直，则这直线与这个平面垂直

　　2．已知直线a、b和平面a ，下列推理中错误的是（　）．

　　A．　　　　　　　　 B．

　　C．　　　　　　　　 D．

　　3．直线a在平面a 内的射影是一个点，那么一定有（　）．

　　A．a∥a　 　　　 B．a⊥a　　　　　　C．aa　 　　　 D．a是a  的斜线

　　4．给出四个命题：

　　①过一点有且只有一条直线与已知平面垂直；

　　②若一条直线与平面a 平行，那么直线上的所有的点到平面的距离相等；

　　③共点O的直线a、b、c两两垂直，那么其中任何一条直线垂直于另两条直线所确定的平面；

　　④如果一条直线垂直于平行四边形的两条边，那么这条直线垂直于这个平行四边形所在的平面．

　　其中正确的命题的个数是（　）．

　　A．3  　　　　　 B．2　　　　　　 　C．1  　　　　　　D．0

　　5．判断下列命题是否正确，并说明理由：

　　（1）a⊥a ，ba a⊥b；

　　（2）AB∥a ，AC⊥a ，BD⊥a AC=BD；

　　（3）a∥b，b⊥a ，ca=a⊥c；

　　（4）线段AB⊥a 于B，线段CD与a 相交于D，则AB≤CD；

　　（5）线段AB、CD在平面a 内的射影为、，若AB=CD，则．

　　6．平面a 的斜线段AB长为6cm，AB在平面a 内的射影长为3cm，则AB所在直线与平面a 所成的角等于________．

　　7．在正方体中，

　　（1）与垂直的棱有________条；

　　（2）与垂直的面对角线有________条；

　　（3）与垂直的棱有________条；

　　（4）与垂直的面对角线有________条．

　　8．直线a、b与平面a 所成的角都等于60°，a、b的位置关系如何?画图说明．

　　9．已知等边三角形ABC的边长为a，D是BC边中点，PA⊥AB，PA⊥AC，且PA=a （如图9-27）．问PD是否与BC垂直?说明理由，并求点P到BC的距离．

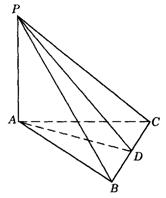
图9-27

　　10．O是平行四边形ABCD两对角线的交点，P 平面ABCD，且PA=PC，PB=PD．

　　求证：PO⊥平面ABCD．

参考答案

　　1．D．

　　2．C．

　　3．B．

　　4．A．其中①、②、③正确．在③中，由于b∩c=P，∴  过b、c确定一个平面a，∵　a⊥b，a⊥c，ba ，ca ，b∩c=P，∴  a⊥a ．④不正确是因为平行四边形的两组对边平行，若直线垂直于平行四边形的两条对边，不能确定直线与平行四边形所在平面垂直．若直线垂直平行四边形的两条邻边，则直线垂直于平行四边形所在的平面．

　　5．（1）正确．

　　　（2）正确．

　　　（3）正确．

　　　（4）不正确．AB、CD可能不是从一个点出发的垂线段与斜线段，长度间无确定关系．

　　　（5）不正确．理由同上．

　　6．60°．

　　7．（1）8条，其中相交垂直的有AB、AD、、四条，异面垂直的有BC、CD、、四条；

　　（2）4条，与垂直的平面有两个平面ABCD和平面，每个面上有两条对角线，即AC、BD、、；

　　（3）4条．∵　BC⊥平面，∴　，同理、、AD均与垂直；

　　（4）6条．是平面ABCD的一条斜线，∵  ⊥平面ABCD，∴  BD为在平面ABCD内的射影．∵  BD⊥AC，∴  由三垂线定理，，即AC为平面ABCD内与垂直的唯一面对角线，正方体共有六个面，每个面有一条面对角线与异面垂直，所以一共有6条．

　　8．a、b可能平行、相交、异面（图略）．

　　9．如图9-27，∵  △ABC是正三角形，D是BC中点，∴  AD⊥BC，∵  PA⊥AB，PA⊥AC，∴  PA⊥平面ABC．∴  AD是PD在平面ABC内的射影，∵　AD⊥BC，根据三垂线定理，PD⊥BC，∴  PD为P点到BC的距离．∵　PA⊥平面ABC，AD平面ABC，∴　PA⊥AD．在Rt△PAD中，AD是正三角形的高，∴　，又∵　PA=a，∴ 

．

　　10．由PA=PC，故△PAC是等腰三角形，又O是AC中点，故PO⊥AC．因此可证PO⊥BD，又AC∩BD=O，因此PO⊥平面ABCD．