高二数学学期期末调研检测试卷

高二数学学期期末调研检测试卷

一、　　　  选择题 (每小题5分，共60分)

1、过空间已知直线外一点作这条直线的垂线　　　　（　　）

　A、有一条 　 B、有两条　C、有无数条　 D、以上三种情况都不对

2、两条直线l₁和l₂关于直线y=x对称，若l₁的方程是y=kx+b(k≠b, b≠0)，那么l₂的方程是　　　　　（　　）

A、　B、　C、 D、

3、两圆x²+y²-10x-10y=0, x²+y²+6x+2y-40=0的公切线的长是　　　　（　　）

A、6 　　　 B、8 　　　 C、10 　　　D、12

4、椭圆的准线方程是　　　　　（　　）

A、 　　 B、  　　C、 　　D、

5、如果双曲线上一点p到双曲线右焦点的距离等于8，那么点p到右准线的距离是　　　（　　）

A、 　　 B、 　　 C、　　 D、10

6、准线方程为y=2的抛物线方程是　　　　（　　）

A、x²=-4y　　B、x²=-8y　　 C、x²=4y　　D、x²=8y

7、曲线与曲线的　　（　　）

A、长轴和短轴相等 　 B、离心率相等 　 C、准线相同　 D、焦距相等

8、设直线a、b 分别是长方体的相邻两个面的对角线所在的直线，则a与b　　（　　）

A、平行　　B、相交 　 C、是异面直线　　 D、可能相交，也可能是异面直线

9、P是四边形ABCD所在平面外一点，连接PA、PB、PC、PD，在四个三角形△PAB、△PBC、△PCD、△PDA中，直角三角形最多可有　　（　　）

A、1个　　　B、2个　　　C、3个　　 D、4个

10、两个平面平行，a ，下列四个命题中，（1）a与 内的所有直线平行；（2）a与 内的无数条直线平行；（3）a与 内的任何一条直线都不垂直；（4）a与无公共点。其中真命题的个数是　

A、　　　　 1　　B、2　　  C、3　　 D、4

11、PO⊥平面ABC，O为垂足，∠CAB＝30°，BC＝5，PA＝PB＝PC＝10，则PO的长等于　　（　　）　　　

A、5　　 B、　　 C、10　　D、10

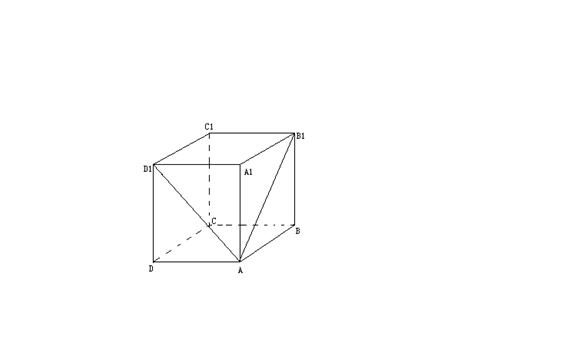
12、如图，在长方体ABCD－A₁B₁C₁D₁中，∠D₁AD＝45°，∠B₁AB＝60°，则∠B₁AD₁的余弦值为　　（　　）

A、 　　　　　 B、　

C、　　　　　　 D、

二、填空题 (每小题4分，共16分)

13、一个点到(4,0)的距离等于它到y轴的距离，则这个点的轨迹方程___________________。

14、已知二面角－－是45°，点P在半平面内，点P到半平面的距离是10cm，则点P到棱的距离是_______________。

15、三棱柱的底面是边长为4cm的正三角形，侧棱长为3cm，一条侧棱与底面相邻两边都成60°的角，则这棱柱的侧面积是____________________。

16、在约束条件2x+5y≥10，2x-3y≥-6，2x+y≤10 下， z=x²+y²的最大值是____________。

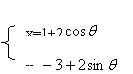三、解答题 (17、18题，每题10分； 19、20题，每题12分；　21题16分，22题14分，共74分)。

17、已知曲线C的参数方程为　　　　　　　　　 ，

(1) 将曲线C的参数方程化为普通方程；

（2）求曲线的斜率为1的切线的方程。

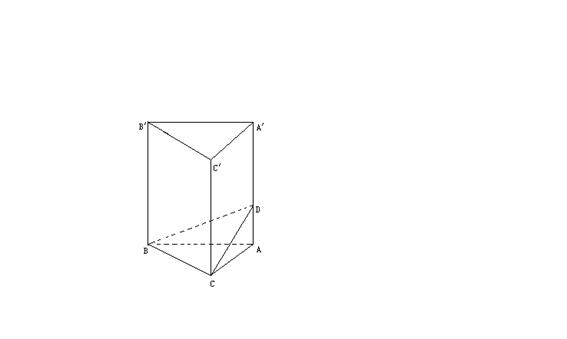18、如图，正三棱柱的底面是边长是6cm，过BC的一个平面的一个平面与底面成30°的二面角，交侧棱AA′于D，求AD的长和截面△BCD的面积。

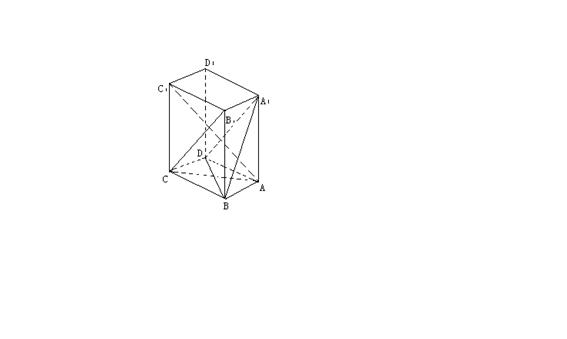
19、如图，在斜四棱柱ABCD-A₁B₁C₁D₁中，底面ABCD为菱形，平面AA₁C₁C⊥底面ABCD，异面直线B₁C与AC₁互相垂直。

(1) 求证：A C₁⊥BD；　　　 (2) 求证：A C₁⊥面A₁BD　

20、有一个椭圆，其中心在原点，焦点在同一坐标轴上，焦距为，一双曲线和这椭圆有公共焦点，且双曲线的半实轴长比椭圆的半长轴长小4，双曲线的离心率与椭圆的离心率之比为7：3，求椭圆和双曲线的方程。

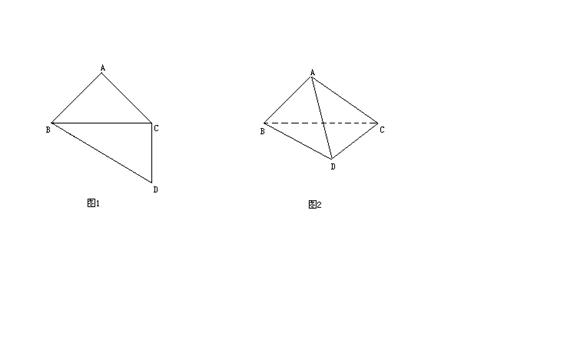21、如图，把一副三角形板拼接(如图1)，BC=6cm，∠BAC=90°，AB=AC，∠BCD=90°，∠BDC=60°，再把两块三角板沿BC折成直二面角(如图2)。

(1) 求证：平面ABD⊥平面ADC； (2) 求直线AD和平面BCD所成二面角的大小；

(3) 求二面角A-BD-C的大小；　　(4) 求直线AD和BC所成角的大小。

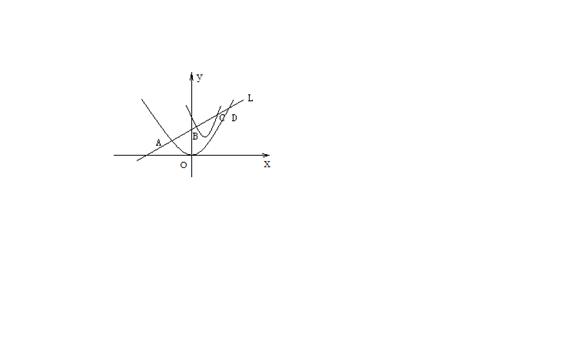
22、已知抛物线C₁：y=x²；C₂：y=2x²-3x+3；直线l:y=kx+m，l与C₁、C₂都相交，如图所示A、B、C、D为从左至右的四个交点。

(1) 当k固定时，求证AB-CD为定值；

(2) 当k=1时，求证AB+CD=(

(3) 在k=1的条件下，m取怎样的值时，AB+CD取最小值，最小值是多少？

参考答案：

一、选择题

1、C　　2、D　　3、C　　4、A　　5、C　　6、B　

7、D　　8、D　　9、D　 10、B　 11、B　　12、D

二、填空题

13、y²=8x-16　 14、　 15、12+12　16、25

三、解答题

17、(1)　(x-1)²+(y+3)²=4　　(2)　x-y-4=0

18、AD=3　S_△BCD=18

19、略

20、当焦点在x轴上时：

当焦点在x轴上时：

21、略

22、略