高二下学期期末数学考试试题
第I卷(选择题,共60分)
一,选择题:本大题共12小题;每小题5分,共60分。在每小题给出的四个选项中,有且只有一项是符合题目要求。
1.设U={0,1,2,3,4},集合A={0,1,2,3},集合B={2,3,4},则![]() ( )
( )
A.{0} B.{0,1} C.{0,1,4} D.{0,1,2,3,4}
2.不等式![]() 的解集是 ( )
的解集是 ( )
![]()
![]()
![]()
![]() 或
或![]()
3.设p:大于![]() 的角叫钝角,q:三角形三边的垂直平分线交于一点。则p、q的复合命题的真假是( )
的角叫钝角,q:三角形三边的垂直平分线交于一点。则p、q的复合命题的真假是( )
A、“p或q”假 B、“p且q”真 C、“非q”真 D、“p或q”真
4.使![]() 成立的x的一个变化区间是( )
成立的x的一个变化区间是( )
![]()
![]()
![]()
![]()
5.将函数y=x+2的图象L按![]() (6,-2)平移后
(6,-2)平移后![]() 的解析式为( )
的解析式为( )
A.y=x+10 B。y=x
6.长方体一个顶点上三条棱的长分别是3、4、5,且它的八个顶点都在同一球面上,这个球的表面积是( )
![]()
![]()
![]()
![]()
7.(文科)已知![]() (2,-3,5),
(2,-3,5), ![]() (-3,1,-4),则
(-3,1,-4),则![]() =( )
=( )
A.(-1,0,1) B.(-1,-2,1) C.(-1,2,1) D.(-1,-2,-1)
(理科)下面有四个命题:
(1)“直线a,b为异面直线”的充分非必要条件是“直线a,b不相交”
(2)“直线L![]() 平面
平面![]() 内所有直线”的充要条件是“
内所有直线”的充要条件是“![]() ”
”
(3)“直线a![]() 直线b”的充分非必要条件是“a垂直于b在
直线b”的充分非必要条件是“a垂直于b在![]()
![]() 内的射影”
内的射影”
(4)“直线a//平面![]() ” 的必要非充分条件是“直线a平行于平面
” 的必要非充分条件是“直线a平行于平面![]() 内的一条直线”。其中正确命题的序号是( )
内的一条直线”。其中正确命题的序号是( )
A.(1) (3) B、(2) (4) C、(2) (3) D、(2) (3) (4)
8.在平行四边形ABCD中,![]() 等于( )
等于( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9.设二项式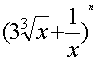 的展开式的各项系数的和为p,所有二项式系数的和为s,若p+s=272,则n等于( )
的展开式的各项系数的和为p,所有二项式系数的和为s,若p+s=272,则n等于( )
A、7 B、
10.对于实数x、y,定义新运算x*y=ax+by,其中a、b是常数,等式右边是通常的加法和乘法运算。若3*5=8,2*5=7,则8*8=( )
A.13 B、
11.设函数![]() ,若存在某个实数m,使f(m)〈0,则f (m+1)〉的值是( )
,若存在某个实数m,使f(m)〈0,则f (m+1)〉的值是( )
A.大于0 B、小于
12.某旅游开发区重视环境保护,绿色植被面积呈上升趋势,经调查,从1993年到2002年这10年间每两年上升2%;已知2001年和2002年种植植被为815万平方米。当地主管部门决定今后4年内仍按这个比例发展下去,那么从2003年到2006年种植的绿色植被为(四舍五入)( )万平方米。
A、848 B、
第![]() 卷(非选择题,共90分)
卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分。
13.若![]() 则z=6x+8y的最大值是
则z=6x+8y的最大值是
14.长方体![]() 中,若
中,若 ![]() ,则直线
,则直线![]() 与
与![]() 所成角的大小为
所成角的大小为
15.设全集U={1,2,3,4,5,6},A 与 B是 U的子集,若![]() ,则称(A,B)为“理想配集”。则所有“理想配集”的个数是
,则称(A,B)为“理想配集”。则所有“理想配集”的个数是
16.白老师在黑板上画出了一条曲线,让同学们各说出它的一条性质。甲、乙、丙、丁四名同学回答如下:甲:曲线的对称轴为坐标轴;乙:曲线过(0,2);丙:曲线的一个焦点是(4,0);丁:曲线的一个顶点是(5,0)。白老师说四人中有一人的回答是错误的。请你写出该曲线的方程 (只需写出一个方程即可)
三.解答题:本大题共6小题,共74分。解答应写出必要的文字说明、证明过程或演算步骤。
17(12分).已知![]() =(-2,1),
=(-2,1),![]() =(2,2),
=(2,2),![]() =(1,2),并且
=(1,2),并且![]() 与
与![]() ,
,![]() 与
与![]() 的夹角分别是
的夹角分别是![]() ,求
,求![]() 的值。
的值。
18(12分)。二月份以来,在我国广东地区发现首例非典病人后,全国二十余省市先后发现非典疑似病例和临床诊断病例。为保护人民的生命财产,增强全民的自我防范意识,某市决定举办抗非知识竞赛,经过层层选拔,某校甲乙二人组合取得决
赛资格。 决赛共有8个不同的题目,其中选择题5个,判断题3个,甲、乙二人依次各抽一题,问(1)甲抽到选择题、乙抽到判断题的概率为多少?(2)甲、乙二人中至少有一个抽到选择题的概率是多少?
 19(12分).如图,直三棱柱
19(12分).如图,直三棱柱![]() 的底面
的底面![]() 中,CA=CB=1,
中,CA=CB=1,![]() ,棱
,棱![]() ,M、N分别为
,M、N分别为 ![]() 的中点。(1)求BN的长(2)
的中点。(1)求BN的长(2)
求异面直线![]() 与
与![]() 所成的角(3)求
所成的角(3)求
证:![]()
20(12).某轮船公司争取到一个相距1000海里的甲、乙两地的客运航线权。已知轮船限载人数为400人,轮船每小时使用的燃料费用与轮船速度的立方成正比例,轮船的最大时速为小时25海里。当船速为每小时10海里时,它的燃料费用是每小时30元;其余费用(不论速度如何)都是每小时480元。你能为该公司设计一种较为合理的船票价格吗?(假设公司打算从每个顾客身上获得平均利润为a元,轮船航行时均为满客)
21 (12分).已知某椭圆的焦点是![]() 过点
过点![]() 并垂直于X轴的直线与椭圆的一个交点为B,且
并垂直于X轴的直线与椭圆的一个交点为B,且![]() 。椭圆上不同的两点
。椭圆上不同的两点![]() 满足:
满足:![]() 成等差数列。(1)求该椭圆的方程。(2)求弦AC中点的横坐标。
成等差数列。(1)求该椭圆的方程。(2)求弦AC中点的横坐标。
22(14分).设f(x)的定义域为![]() 且
且![]() 且
且![]() 如果f(x)为奇函数,当
如果f(x)为奇函数,当![]() 。
。
(1)求![]()
(2)当![]() 时,求f(x);
时,求f(x);
(3)是否存在这样的正整数k,使得![]() 时,
时,![]() 有解。
有解。
弥勒一中2002——2003高二数学期末测试答案
一.选择题(每题5分,共60分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| C | A | D | A | B | C | B | C | D | D | A | C |
| 二. 13题 40 14题 15题 27 16题 |
| |
| ||
| 三.答题 17题(12分) 解:因为 所以 又
又
| ||
| 18题(12分) 解:(1)甲、乙二人依次从8个题目中各抽一题的基本事件数为
(2)
|
| |
| 19题(12分)
解:(文科)(1)以C为坐标原点CA为X轴的正半轴、CB为Y轴的正半轴建立空间直角坐标系,则B(0,1,0),N(1,0,1) (2分) (2) (3) (理科)(1) 则 (2)采用割补的思想,将三棱柱补成四棱柱,显然 则所求为 (3)
需要特别指出的是:因本大题解法多样,同学只要做对即可给分。
|
| |
| 20题(12分) 解:设轮船以每小时 又设每小时的燃料费为y,则y= 由
因此,轮船航行完全程的总费用为
= =36000 (9分) 当且仅当 故该公司的船票价格应定为每张(90+a)元。 (12分) |
|
| 21题(12分) 解:(1) (2)由点 又椭圆的右准线方程为 由 设弦AC的中点为 | |
22题(14分)
解:![]() (2分)
(2分)
![]() 是周期为2的周期函数
(4分)
是周期为2的周期函数
(4分)
![]() (6分)
(6分)
(2)![]() 解:(1)
解:(1)![]() (3分)
(3分)![]()
![]()
![]()
![]() (8分)
(8分)
又![]() (10分)
(10分)
![]() (12分)
(12分)
(3)由![]() 及(2)有
及(2)有
![]() 即
即
![]() (*)
(*)
![]()
当k=1时,![]() =0,(*)无解
=0,(*)无解
当![]() 时,(*)的解为
时,(*)的解为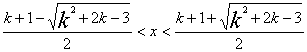 且
且![]() 又
又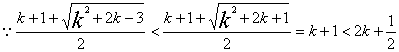
![]()
![]() 故不存在满足条件的正整数k。 (14分)
故不存在满足条件的正整数k。 (14分)
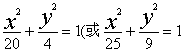 )
)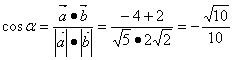 (5分)
(5分)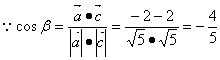 (8分)
(8分)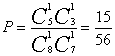 ( 6分)
( 6分)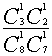 (8分)
(8分)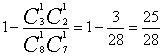 (12分)
(12分)
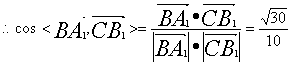 (7分)
(7分)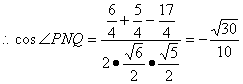
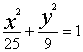 (6分)
(6分)